《初階數據結構》尾聲

前言：

《快速排序（非遞歸）》:

《歸并排序》：

《歸并排序（非遞歸）》：

《計數排序》：

對于快速排序的優化：

分析：

總結：

前言：

上一篇blog重點講解了《選擇排序》《插入排序》，重點介紹了快速排序的三種方法，這篇blog主要講解《歸并排序》以及它的非遞歸使用方法，最后還會再補充一個計數排序。

上一篇的blog:《插入排序》與《選擇排序》-CSDN博客

《快速排序（非遞歸）》:

typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort3(a, left, right);//分區間[left, keyi-1] keyi [keyi+1, right]if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}}STDestory(&s);
}

我們目前學習數據結構到此，由于我們呢接觸了不少的遞歸操作，不難發現，其實遞歸的算法與棧這個數據結構較為類似。

我們還是一樣先對整體進行排序，分別將begin和end入棧，然后設置好left和right。在第一次對總體排完序后，還是一如既往的會分出兩個區間，我們又需要分別對左右兩個區間進行排序。

在我們利用棧執行代碼的時候要注意先后順序，先入棧的后后訪問，后入棧的先訪問。

《歸并排序》：

歸并排序（MERGE-SORT）是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法（Divide andConquer）的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。

void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end){return;}int mid = (end + begin) / 2;//[begin, mid] [mid + 1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);int begin1 = begin;int end1 = mid;int begin2 = mid + 1;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])//<=才是穩定的{tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int)* (end - begin + 1));}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)* n);if (tmp == NULL){perror("tmp -> malloc");exit(-1);}_MergeSort(a, 0, n - 1, tmp);}

?所謂歸并，就是分而治之。

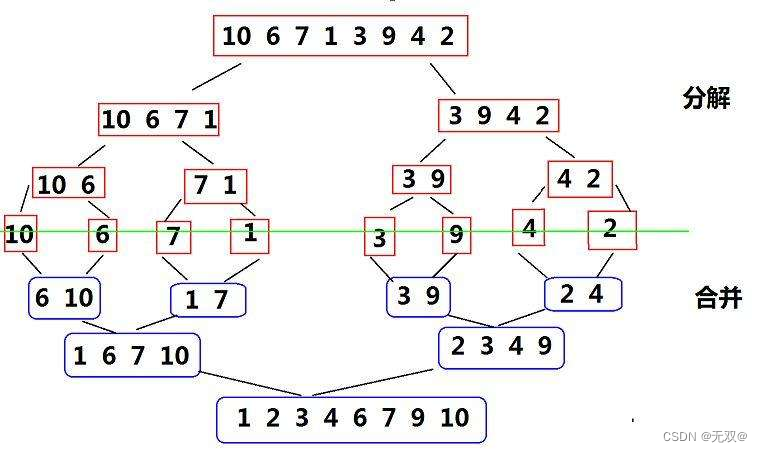
我們使用遞歸來實現數組的分割和合并，它的邏輯非常像二叉樹的后序遍歷，由于我們要使用遞歸，又要申請臨時空間，所以我們先申請好臨時空間，再將歸并排序過程作為子函數調用，這樣不用在每次遞歸過程申請釋放空間

《歸并排序（非遞歸）》：

我們在快速排序的非遞歸中運用了棧這一數據結構，而我們在實現歸并排序中，不可以去使用棧這一數據結構。

首先我們要知道，如果我們不用棧，我們可以用哪些方法替代，一個我們熟知的方法，是棧，還有一個則是循環。

那么話說回來，為什么不能用棧呢？

對于歸并排序來說，與我們在二叉樹所介紹的后序遍歷較為相似，屬于是“先把每條路走了，再回來說再見”。相比較于快速排序，利用棧是先對總體進行排序，再分區間進行排序。

而歸并排序呢，一上來就把左區間給排完了，那右區間該怎么找呢？出棧后還要在歸并的過程中再次使用出棧后的子區間。

所以我們需要利用循環來進行處理。

我們可以理解我從底層向上拓展，所以我們一開始是1個數據和1個數據進行比較，就像：

我們可以設置一個gap，就像希爾排序那樣，只不過這次我們需要利用這個gap來限制end和begin

我們初始化gap == 1，意思就是兩兩比較，a[0]與a[1]比較分出大小，a[1]與a[2]比較分出大小，最后當下標越界了的時候，我們就可以開始對四個四個之間進行比較，讓gap*=2即可分好下一個小組。

void MergeSortNoR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)* n);if (tmp == NULL){perror("tmp -> malloc");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;if (end1 >= n || begin1 >= n){break;}if (end2 >= n){end2 = n - 1;}int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int)* (end2 - i + 1));}gap *= 2;}}

《計數排序》：

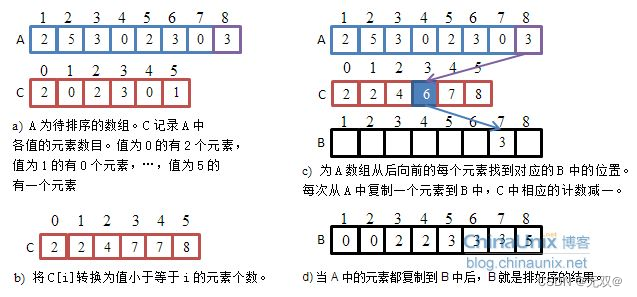
計數排序又稱為鴿巢原理，是對哈希直接定址法的變形應用。操作步驟：
1. 統計相同元素出現次數
2. 根據統計的結果將序列回收到原來的序列中

void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));//計數for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}}

這里我們做了一個優化，假設我們要排序2,3,8888,6666,諸如這樣間隔相差很大的數字，如果不做優化處理就直接calloc新數組，那么會造成許多的空間浪費，所以減去最小值，減小空間的浪費。

這種排序的局限性集中于：

1.不適合分散的數據，適合集中的數據。

2.不適合浮點數、字符串、結構體數據排序，只適合整數。

對于快速排序的優化：

假設每次取的關鍵字key恰好是最大值或者最小值，即數組已經有序，這時的時間復雜度就是O(N^2)

所以我們可以找到最左邊，最右邊，和中間值，進行三數取中，誰不大不小就讓誰做關鍵字并且與第一個數進行交換。

int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[midi] < a[begin]){if (a[end] < a[midi]){return midi;}else if (a[begin] < a[end]){return begin;}else{return end;}}else //a[midi]>a[begin]{if (a[end] > a[midi]){return midi;}else if (a[begin] > a[end]){return begin;}else{return begin;}}
}

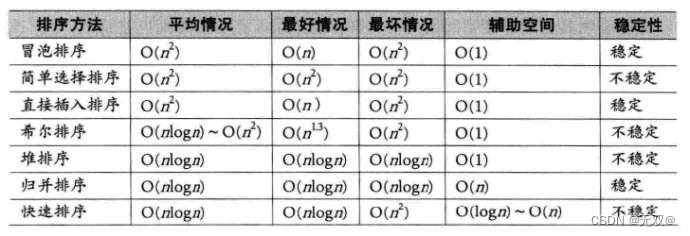
分析：

我們可以通過隨機生成100000個數來進行效率的測試。

//測試效率
void TestOp()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int)* N);int* a2 = (int*)malloc(sizeof(int)* N);int* a3 = (int*)malloc(sizeof(int)* N);int* a4 = (int*)malloc(sizeof(int)* N);int* a5 = (int*)malloc(sizeof(int)* N);int* a6 = (int*)malloc(sizeof(int)* N);int* a7 = (int*)malloc(sizeof(int)* N);int* a8 = (int*)malloc(sizeof(int)* N);int* a9 = (int*)malloc(sizeof(int)* N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a9[i] = a1[i];}for (int i = 0; i < N; i++){a8[i] = i;}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin9 = clock();CountSort(a9, N);int end9 = clock();printf("InsertSort(直接插入排序):%d\n", end1 - begin1);printf("ShellSort(希爾排序):%d\n", end2 - begin2);printf("SelectSort(選擇排序):%d\n", end3 - begin3);printf("HeapSort(堆排序):%d\n", end4 - begin4);printf("QuickSort(快速排序):%d\n", end5 - begin5);printf("MergeSortSort(歸并排序):%d\n", end6 - begin6);printf("CountSort(計數排序):%d\n", end9 - begin9);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a9);
}