一、容斥原理
容斥原理公式
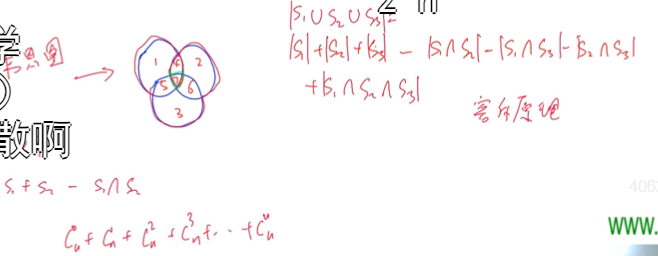
一共加或者減的式子個數
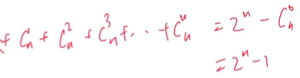
?![]()
(一)利用容斥原理解決求能被質數整除的數的個數
890計算能被整除的數的個數
因為一共有2^n-1種選法,可以用位運算的方式枚舉,對于得到的每一種選法,根據存在的數的個數判斷前面是1還是-1。枚舉到2^n-1的所有二進制數,判斷每一位上的數是否是1,
最重要的轉變是:將能被各個質數整除的集合看成一個個的集合。根據容斥原理,需要計算各個集合的組合方式的元素個數然后相加。在找組合方式的時候因為一共有2^n-1種,可以用m位的二進制數表示。如何計算一個一個組合的可以整除的個數。一位一位右移&1判斷。
#include<bits/stdc++.h>
//890 求能被質數整除的數
using namespace std;
typedef long long LL;
const int N=20;
int n,m;
int p[N];
int main()
{cin>>n>>m;//讀入所有的質數for(int i=0;i<m;i++)cin>>p[i];int res=0;//遍歷所有二進制數for(int i=1;i<1<<m;i++){int cnt=0;int t=1;//遍歷這個二進制數的所有位for(int j=0;j<m;j++){if(i>>j&1){//記錄當前選擇集合的個數cnt++;//并將集合元素相乘t*=p[j];//如果n一倍的t都裝不了就breakif(t>n){t=-1;break;}}}if(t!=-1){if(cnt%2)res+=n/t;else res-=n/t;}}cout<<res<<endl;}
二、博弈論
891 先手是否先獲勝
![]()
結論:

如果異或值不是0,先手可以拿一堆石子兒讓拿之后狀態變成必輸。
異或不會產生1,只會消除1。

因為異或上x之后會ai一定會變小,也就是這一堆石子兒是可以讓棋手拿的。最后剩余ai異或x。整個式子異或之后是0.也就是可以進行一次操作并得到一個對手必敗的局面(不管對手怎么去拿異或之后都不為0)。也就是先手先勝利。
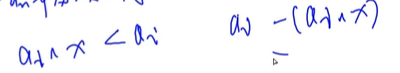
先手遇到的總不是0,后手遇到的總是0,最后后手敗。
#include<bits/stdc++.h>
//891 Nim游戲
using namespace std;
typedef long long LL;
int main()
{int n;cin>>n;int res=0;while(n--){int x;cin>>x;res^=x;}if(res)puts("Yes");else puts("No");return 0;
}
三、sg函數
mex是某個點的出邊指向的所有點的值(不再其中)的最小的自然數。

如果sg不為0,就說明有出邊指向0
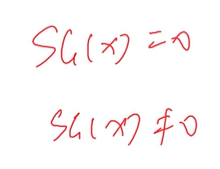
nim游戲和sg函數含義相似。每個結點的sg函數可以看做一個小石頭堆。nim游戲中異或之后如果不等于0,可以找到ai,拿走ai-ai^x。最后得到的狀態就是0。在sg中。如果異或之后的值非0,和nim一樣,將其變成ai^x。因為?ai^x<ai.所以一定有一個出邊指向ai^x成立,并且之后的狀態變成0.
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_set>
using namespace std;
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];
int sg(int x)
{if (f[x] != -1) return f[x];unordered_set<int> S;for (int i = 0; i < m; i ++ ){int sum = s[i];if (x >= sum) S.insert(sg(x - sum));}for (int i = 0; ; i ++ )if (!S.count(i))return f[x] = i;
}int main()
{cin >> m;for (int i = 0; i < m; i ++ ) cin >> s[i];cin >> n;memset(f, -1, sizeof f);int res = 0;for (int i = 0; i < n; i ++ ){int x;cin >> x;res ^= sg(x);}if (res) puts("Yes");else puts("No");return 0;
}









)


)


)


