Leetcode?62.不同路徑

題目鏈接：62 不同路徑

題干：一個機器人位于一個?m x n?網格的左上角 （起始點在下圖中標記為 “Start” ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 “Finish” ）。問總共有多少條不同的路徑？

思考一：動態規劃。

• 確定dp數組（dp table）以及下標的含義

dp[i][j] ：表示從（0 ，0）出發，到(i, j) 有dp[i][j]條不同的路徑。

• 確定遞推公式

從dp[i][j]的定義可以看出，只能有兩個方向來推導出來，即dp[i - 1][j]向右走 和 dp[i][j - 1]向下走。

所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

• dp數組的初始化

首先dp[i][0]一定都是1，因為從(0, 0)的位置到(i, 0)的路徑只有一條，dp[0][j]也同理。代碼如下：

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

• 確定遍歷順序

從遞歸公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1];中可以看出，dp[i][j]是依賴 dp[i - 1][j]和 dp[i][j - 1]，那么遍歷的順序一定是從左到右一層一層遍歷的。

• 舉例推導dp數組

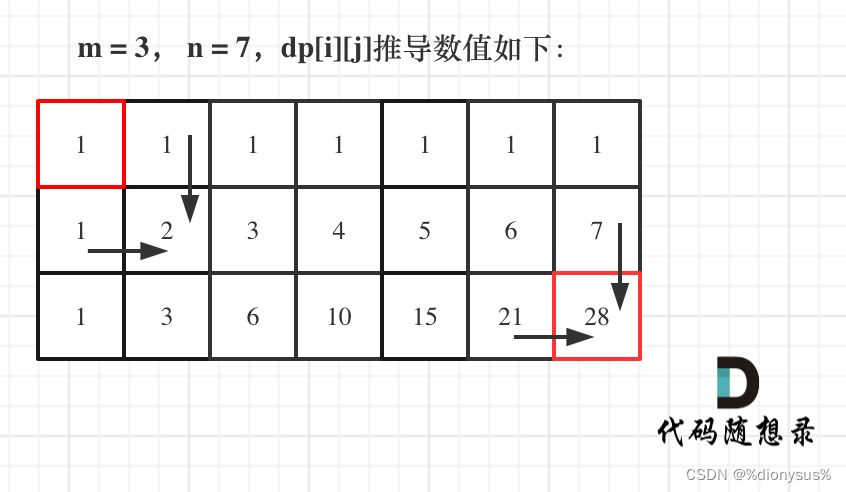
代碼：

class Solution {
public:int uniquePaths(int m, int n) {int dp[m][n];       //記錄到達下標（i，j）的路徑數//初始化for (int i = 0; i < m; i++)     //從起始點一直到最右邊只存在一條路徑dp[i][0] = 1;for (int j = 0; j < n; j++)     //從起始點一直到最下邊只存在一條路徑dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];     //遞推公式}return dp[m - 1][n - 1];}
};

優化：其實用一個一維數組（可以理解是滾動數組）即可，可以優化空間。

代碼：

class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;        //初始化for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {        //處理每列元素dp[i] += dp[i - 1];}}return dp[n - 1];}
};

思考二：深度優先搜索。題目中說機器人每次只能向下或者向右移動一步，那么其實機器人走過的路徑可以抽象為一棵二叉樹，而葉子節點就是終點！如圖：

但如果只是按以上思路同一位置多次計算，會超時。因此要加上備忘錄，初始化為-1。終止條件加上判斷當前位置備忘錄是否記錄過，記錄過則直接返回數據。單層遞歸處理邏輯也要記錄數據。?

代碼：

class Solution {
public:vector<vector<int>> memo;       //添加備忘錄int dfs(int row, int col, const int m, const int n) {if (row > m || col > n) return 0;       //超出邊界返回0if (row == m && col == n)   return 1;   //搜索到一條路徑if (memo[row][col] != -1)   return memo[row][col];      //訪問過則直接返回記錄值int right = dfs(row + 1, col, m, n);        //向右移動int down = dfs(row, col + 1, m, n);         //向下移動memo[row][col] = right + down;      //記錄數據return memo[row][col];  }int uniquePaths(int m, int n) {if (m < 1 || n < 1) return 0;memo = vector<vector<int>>(m + 1, vector<int>(n + 1, -1));return dfs(1, 1, m, n);}
};

思考三：數論法。

在下圖中，可以看出一共m，n的話，無論怎么走，走到終點都需要 m + n - 2 步。

在這m + n - 2 步中，一定有 m - 1 步是要向下走的，不用管什么時候向下走。

那么路徑問題就轉換為，給你m + n - 2個不同的數，隨便取m - 1（或n - 1）個數，有幾種取法。

這便是組合問題。答案為或，取較小值計算。

求組合要防止兩個int相乘溢出。?所以不能把算式的分子都算出來，分母都算出來再做除法。

代碼：

class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1;       //分子int denominator = 1;           //分母int count = m > n ? n - 1 : m - 1;int num = m + n - 2;while (count > 0) {     //邊乘邊除numerator *= num;denominator *= count;if (denominator != 1 && numerator % denominator == 0) {     //可整除numerator /= denominator;denominator = 1;}num--;count--;}return numerator;}
};

Leetcode?63. 不同路徑 II

題目鏈接：63 不同路徑 II

題干：一個機器人位于一個?m x n?網格的左上角 （起始點在下圖中標記為 “Start” ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 “Finish”）。

現在考慮網格中有障礙物。那么從左上角到右下角將會有多少條不同的路徑？

網格中的障礙物和空位置分別用?1?和?0?來表示。

思考一：動態規劃。

和上題的區別僅在障礙物，因此思路僅在確定遞推公式和dp數組的初始化兩步存在差異

• 確定遞推公式

從dp[i][j]的定義可以看出，只能有兩個方向來推導出來，即dp[i - 1][j]向右走 和 dp[i][j - 1]向下走。

正常公式應為dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

但障礙物所在位置不可達，因此在處理前先判斷。代碼如下：

if (obstacleGrid[i][j] == 1)        //此下標位置存在障礙物    continue;       

• dp數組的初始化

由于障礙物的存在，因此只有在未碰到障礙物的前面位置dp[i][0]=1。dp[0][j]也同理。代碼如下：

for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)     //從起始點向右直到碰到邊界或者障礙物只存在一條路徑dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++)     //從起始點向下直到碰到邊界或者障礙物只存在一條路徑dp[0][j] = 1;

代碼：

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起點或終點出現了障礙直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));       //記錄到達下標（i，j）的路徑數   //初始化for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)     //從起始點向右直到碰到邊界或者障礙物只存在一條路徑dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++)     //從起始點向下直到碰到邊界或者障礙物只存在一條路徑dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1)    continue;       //此下標位置存在障礙物dp[i][j] = dp[i - 1][j] + dp[i][j - 1];     //遞推公式}}return dp[m - 1][n - 1];}
};

思考二：深度優先搜索。僅在終止條件這多加碰到障礙物則此條路徑作廢返回0即可。當然還得加上備忘錄減少處理時間。

代碼：

class Solution {
public:vector<vector<int>> memo;       //添加備忘錄int dfs(int row, int col, const int m, const int n, const vector<vector<int>>& obstacleGrid) {if (row > m - 1 || col > n - 1) return 0;       //超出邊界返回0if (obstacleGrid[row][col] == 1)    return 0;       //碰到障礙物返回0if (row == m - 1 && col == n - 1)   return 1;       //搜索到一條路徑if (memo[row][col] != -1)   return memo[row][col];      //訪問過則直接返回記錄值int right = dfs(row + 1, col, m, n, obstacleGrid);      //向右int down = dfs(row, col + 1, m, n, obstacleGrid);       //向下memo[row][col] = right + down;      //記錄數據return memo[row][col];}int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();memo = vector<vector<int>>(m, vector<int>(n, -1));if (m < 1 || n < 1) return 0;return dfs(0, 0, m, n, obstacleGrid);}
};

自我總結：

• 了解到C++備忘錄模式，減少處理時間。