形象易懂講解算法I——小波變換

https://zhuanlan.zhihu.com/p/22450818?refer=dong5

?

最早發于回答：能不能通俗的講解下傅立葉分析和小波分析之間的關系？ - 咚懂咚懂咚的回答
現收入專欄。


從傅里葉變換到小波變換，并不是一個完全抽象的東西，可以講得很形象。小波變換有著明確的物理意義，如果我們從它的提出時所面對的問題看起，可以整理出非常清晰的思路。

下面我就按照傅里葉-->短時傅里葉變換-->小波變換的順序，講一下為什么會出現小波這個東西、小波究竟是怎樣的思路。（反正題主要求的是通俗形象，沒說簡短，希望不會太長不看。。）

一、傅里葉變換
關于傅里葉變換的基本概念在此我就不再贅述了，默認大家現在正處在理解了傅里葉但還沒理解小波的道路上。（在第三節小波變換的地方我會再形象地講一下傅里葉變換）

下面我們主要將傅里葉變換的不足。即我們知道傅里葉變化可以分析信號的頻譜，那么為什么還要提出小波變換？答案就是方沁園所說的，“對非平穩過程，傅里葉變換有局限性”。看如下一個簡單的信號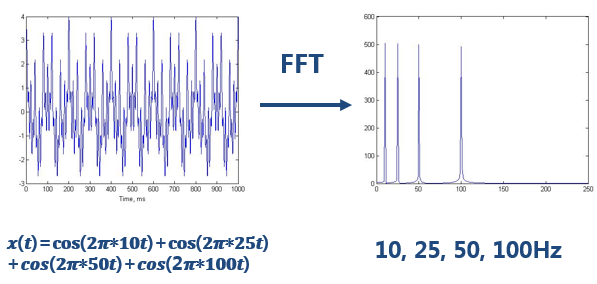：做完FFT（快速傅里葉變換）后，可以在頻譜上看到清晰的四條線，信號包含四個頻率成分。

一切沒有問題。但是，如果是頻率隨著時間變化的非平穩信號呢？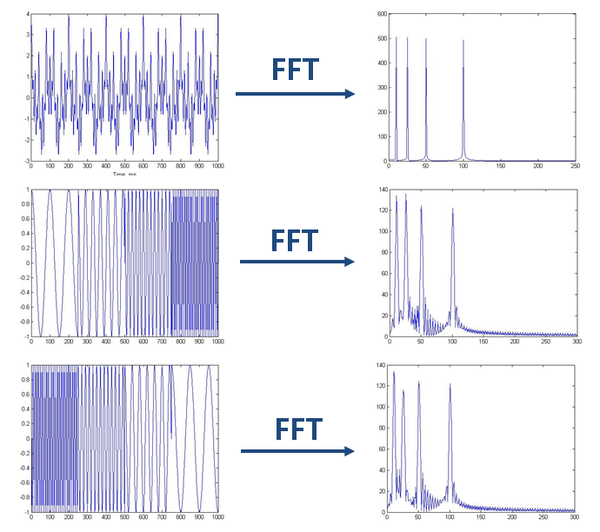

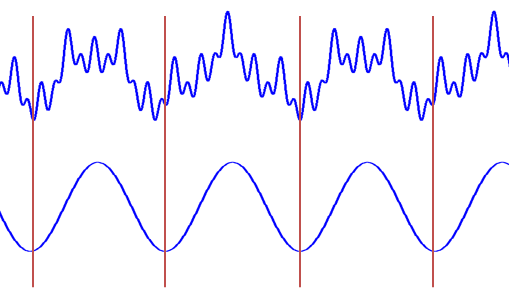
如上圖，最上邊的是頻率始終不變的平穩信號。而下邊兩個則是頻率隨著時間改變的非平穩信號，它們同樣包含和最上信號相同頻率的四個成分。
做FFT后，我們發現這三個時域上有巨大差異的信號，頻譜（幅值譜）卻非常一致。尤其是下邊兩個非平穩信號，我們從頻譜上無法區分它們，因為它們包含的四個頻率的信號的成分確實是一樣的，只是出現的先后順序不同。

可見，傅里葉變換處理非平穩信號有天生缺陷。它只能獲取一段信號總體上包含哪些頻率的成分，但是對各成分出現的時刻并無所知。因此時域相差很大的兩個信號，可能頻譜圖一樣。

然而平穩信號大多是人為制造出來的，自然界的大量信號幾乎都是非平穩的，所以在比如生物醫學信號分析等領域的論文中，基本看不到單純傅里葉變換這樣naive的方法。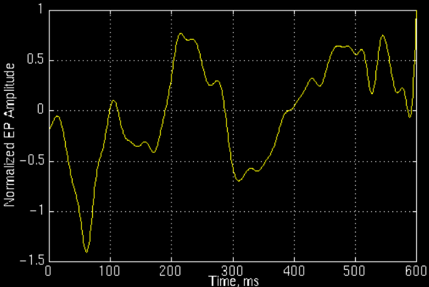
上圖所示的是一個正常人的事件相關電位。對于這樣的非平穩信號，只知道包含哪些頻率成分是不夠的，我們還想知道各個成分出現的時間。知道信號頻率隨時間變化的情況，各個時刻的瞬時頻率及其幅值——這也就是時頻分析。


二、短時傅里葉變換（Short-time Fourier Transform, STFT）
一個簡單可行的方法就是——加窗。我又要套用方沁園同學的描述了，“把整個時域過程分解成無數個等長的小過程，每個小過程近似平穩，再傅里葉變換，就知道在哪個時間點上出現了什么頻率了。”這就是短時傅里葉變換。
看圖：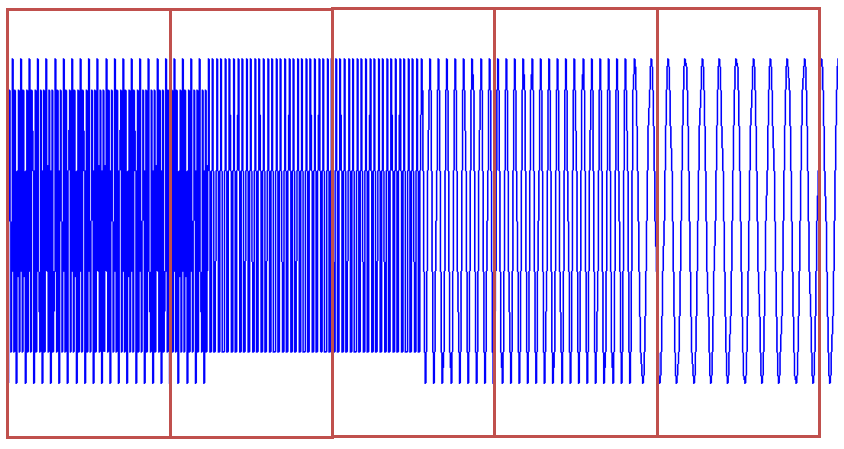
時域上分成一段一段做FFT，不就知道頻率成分隨著時間的變化情況了嗎！
用這樣的方法，可以得到一個信號的時頻圖了：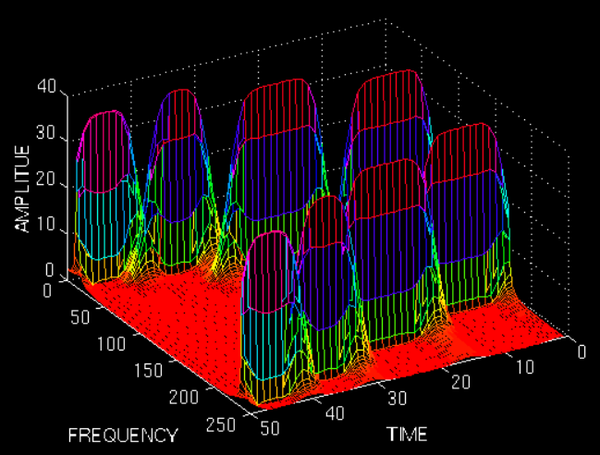
——此圖像來源于“THE WAVELET TUTORIAL”
圖上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四個頻域成分，還能看到出現的時間。兩排峰是對稱的，所以大家只用看一排就行了。

是不是棒棒的？時頻分析結果到手。但是STFT依然有缺陷。

使用STFT存在一個問題，我們應該用多寬的窗函數？
窗太寬太窄都有問題：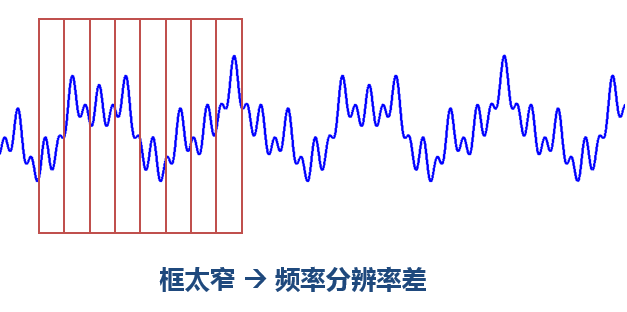
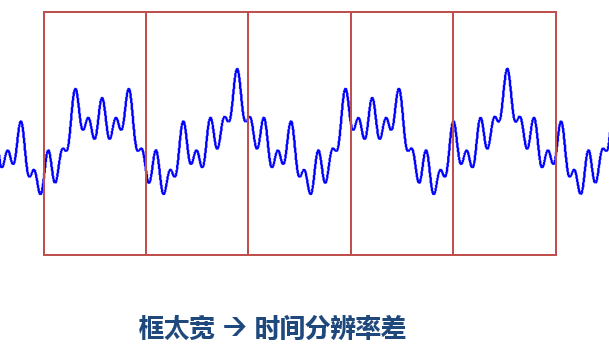窗太窄，窗內的信號太短，會導致頻率分析不夠精準，頻率分辨率差。窗太寬，時域上又不夠精細，時間分辨率低。
（這里插一句，這個道理可以用海森堡不確定性原理來解釋。類似于我們不能同時獲取一個粒子的動量和位置，我們也不能同時獲取信號絕對精準的時刻和頻率。這也是一對不可兼得的矛盾體。我們不知道在某個瞬間哪個頻率分量存在，我們知道的只能是在一個時間段內某個頻帶的分量存在。 所以絕對意義的瞬時頻率是不存在的。）

看看實例效果吧：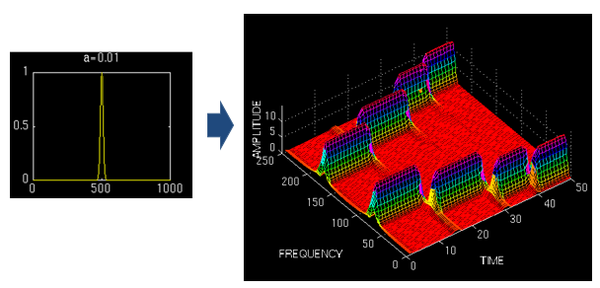
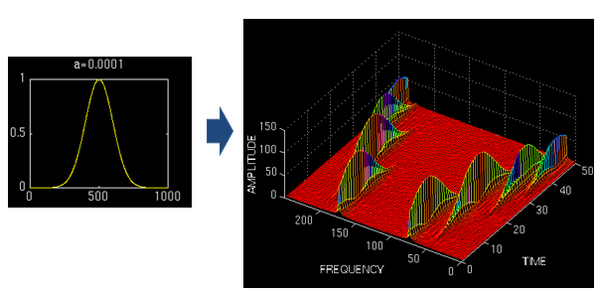
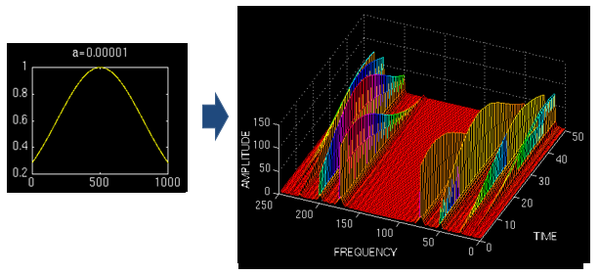——此圖像來源于“THE WAVELET TUTORIAL”
上圖對同一個信號（4個頻率成分）采用不同寬度的窗做STFT，結果如右圖。用窄窗，時頻圖在時間軸上分辨率很高，幾個峰基本成矩形，而用寬窗則變成了綿延的矮山。但是頻率軸上，窄窗明顯不如下邊兩個寬窗精確。

所以窄窗口時間分辨率高、頻率分辨率低，寬窗口時間分辨率低、頻率分辨率高。對于時變的非穩態信號，高頻適合小窗口，低頻適合大窗口。然而STFT的窗口是固定的，在一次STFT中寬度不會變化，所以STFT還是無法滿足非穩態信號變化的頻率的需求。


三、小波變換

那么你可能會想到，讓窗口大小變起來，多做幾次STFT不就可以了嗎？！沒錯，小波變換就有著這樣的思路。
但事實上小波并不是這么做的（關于這一點，方沁園同學的表述“小波變換就是根據算法，加不等長的窗，對每一小部分進行傅里葉變換”就不準確了。小波變換并沒有采用窗的思想，更沒有做傅里葉變換。）
至于為什么不采用可變窗的STFT呢，我認為是因為這樣做冗余會太嚴重，STFT做不到正交化，這也是它的一大缺陷。

于是小波變換的出發點和STFT還是不同的。STFT是給信號加窗，分段做FFT；而小波直接把傅里葉變換的基給換了——將無限長的三角函數基換成了有限長的會衰減的小波基。這樣不僅能夠獲取頻率，還可以定位到時間了~

【解釋】
來我們再回顧一下傅里葉變換吧，沒弄清傅里葉變換為什么能得到信號各個頻率成分的同學也可以再借我的圖理解一下。
傅里葉變換把無限長的三角函數作為基函數：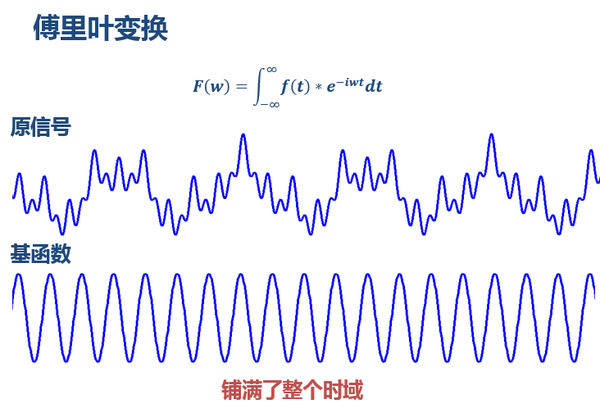

這個基函數會伸縮、會平移（其實本質并非平移，而是兩個正交基的分解）。縮得窄，對應高頻；伸得寬，對應低頻。然后這個基函數不斷和信號做相乘。某一個尺度（寬窄）下乘出來的結果，就可以理解成信號所包含的當前尺度對應頻率成分有多少。于是，基函數會在某些尺度下，與信號相乘得到一個很大的值，因為此時二者有一種重合關系。那么我們就知道信號包含該頻率的成分的多少。

仔細體會可以發現，這一步其實是在計算信號和三角函數的相關性。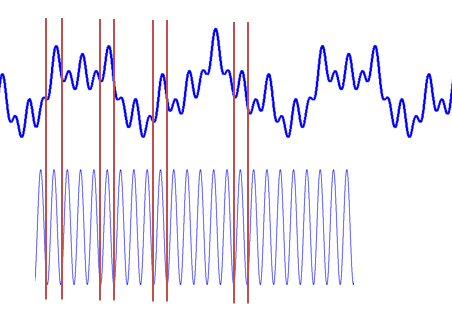

看，這兩種尺度能乘出一個大的值（相關度高），所以信號包含較多的這兩個頻率成分，在頻譜上這兩個頻率會出現兩個峰。


以上，就是粗淺意義上傅里葉變換的原理。




如前邊所說，小波做的改變就在于，將無限長的三角函數基換成了有限長的會衰減的小波基。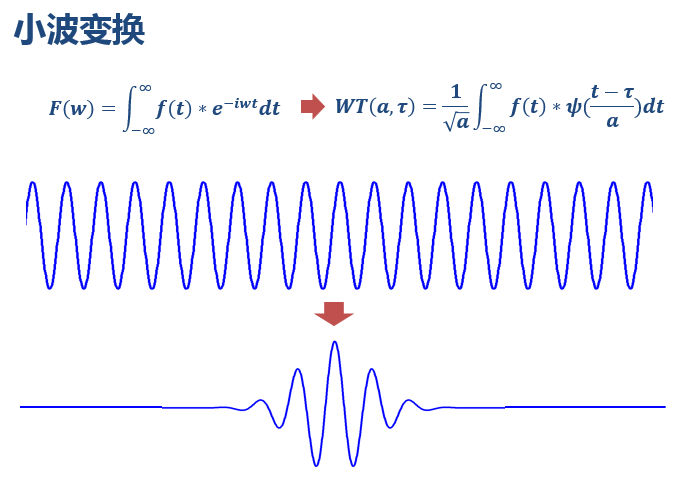
這就是為什么它叫“小波”，因為是很小的一個波嘛~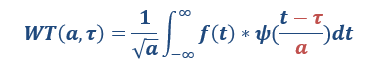


從公式可以看出，不同于傅里葉變換，變量只有頻率ω，小波變換有兩個變量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函數的伸縮，平移量?τ控制小波函數的平移。尺度就對應于頻率（反比），平移量?τ就對應于時間。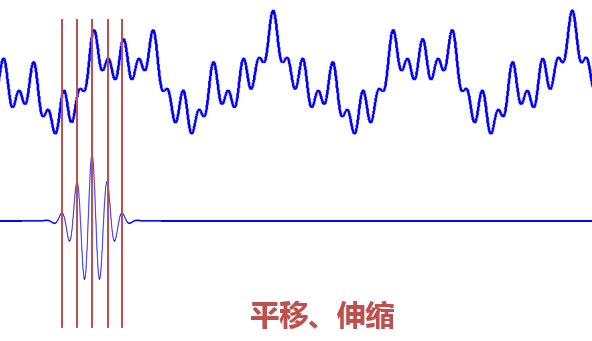



當伸縮、平移到這么一種重合情況時，也會相乘得到一個大的值。這時候和傅里葉變換不同的是，這不僅可以知道信號有這樣頻率的成分，而且知道它在時域上存在的具體位置。

而當我們在每個尺度下都平移著和信號乘過一遍后，我們就知道信號在每個位置都包含哪些頻率成分。

看到了嗎？有了小波，我們從此再也不害怕非穩定信號啦！從此可以做時頻分析啦！

做傅里葉變換只能得到一個頻譜，做小波變換卻可以得到一個時頻譜！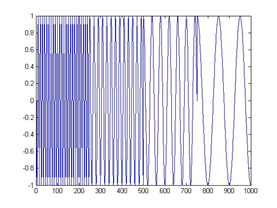
↑：時域信號
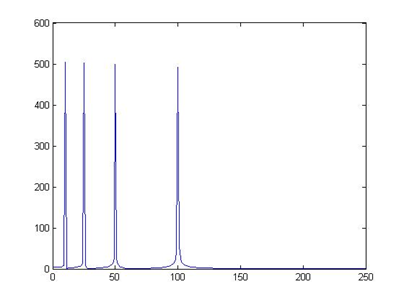↑：傅里葉變換結果

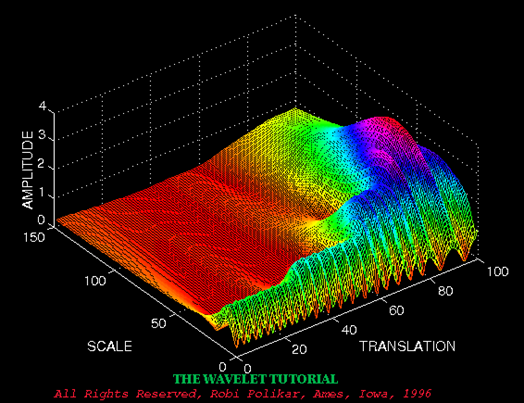——此圖像來源于“THE WAVELET TUTORIAL”
↑：小波變換結果

小波還有一些好處，比如，我們知道對于突變信號，傅里葉變換存在吉布斯效應，我們用無限長的三角函數怎么也擬合不好突變信號：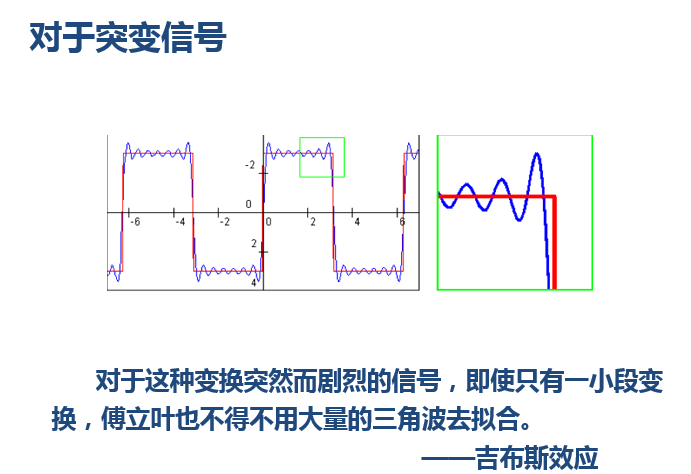
然而衰減的小波就不一樣了：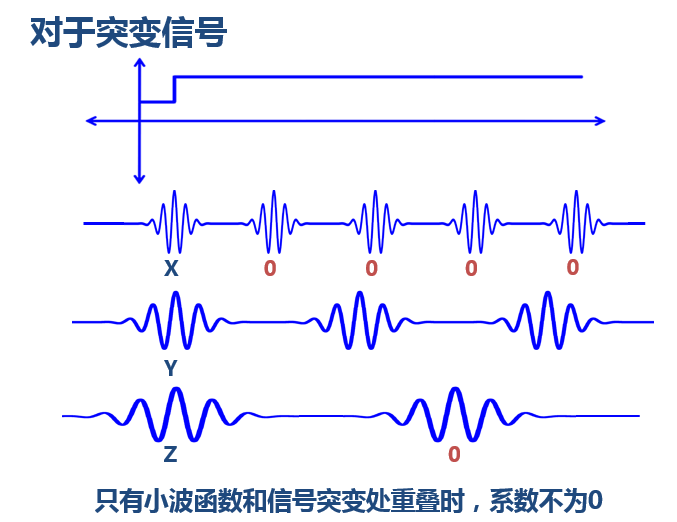




以上，就是小波的意義。

-----------------------------------------------------------------------------------------------------------

以上只是用形象地給大家展示了一下小波的思想，希望能對大家的入門帶來一些幫助。畢竟如果對小波一無所知，直接去看那些堆砌公式、照搬論文語言的教材，一定會痛苦不堪。
在這里推薦幾篇入門讀物，都是以感性介紹為主，易懂但并不深入，對大家初步理解小波會很有幫助。文中有的思路和圖也選自于其中：
1. THE WAVELET TUTORIAL （強烈推薦，點擊鏈接：INDEX TO SERIES OF TUTORIALS TO WAVELET TRANSFORM BY ROBI POLIKAR）
2. WAVELETS：SEEING THE FOREST AND THE TREES
3. A Really Friendly Guide to Wavelets
4. Conceptual wavelets

但是真正理解透小波變換，這些還差得很遠。比如你至少還要知道有一個“尺度函數”的存在，它是構造“小波函數”的關鍵，并且是它和小波函數一起才構成了小波多分辨率分析，理解了它才有可能利用小波做一些數字信號處理；你還要理解離散小波變換、正交小波變換、二維小波變換、小波包……這些內容國內教材上講得也很糟糕，大家就一點一點啃吧~











-------------------------------------------------------------------------------------------------------------------------
一些問題的回答：
1. 關于海森堡不確定性原理
不確定性原理，或者叫測不準原理，最早出自量子力學，意為在微觀世界，粒子的位置與動量不可同時被確定。但是這個原理并不局限于量子力學，有很多物理量都有這樣的特征，比如能量和時間、角動量和角度。體現在信號領域就是時域和頻域。不過更準確一點的表述應該是：一個信號不能在時空域和頻域上同時過于集中；一個函數時域越“窄”，它經傅里葉變換的頻域后就越“寬”。
如果有興趣深入研究一下的話，這個原理其實非常耐人尋味。信號處理中的一些新理論在根本上也和它有所相連，比如壓縮感知。如果你剝開它復雜的數學描述，最后會發現它在本質上能實現其實和不確定性原理密切相關。而且大家不覺得這樣一些矛盾的東西在哲學意義上也很奇妙嗎？


2. 關于正交化
什么是正交化？為什么說小波能實現正交化是優勢?
簡單說，如果采用正交基，變換域系數會沒有冗余信息，變換前后的信號能量相等，等于是用最少的數據表達最大的信息量，利于數值壓縮等領域。JPEG2000壓縮就是用正交小波變換。
比如典型的正交基：二維笛卡爾坐標系的（1,0）、（0,1），用它們表達一個信號顯然非常高效，計算簡單。而如果用三個互成120°的向量表達，則會有信息冗余，有重復表達。
但是并不意味著正交一定優于不正交。比如如果是做圖像增強，有時候反而希望能有一些冗余信息，更利于對噪聲的抑制和對某些特征的增強。

3. 關于瞬時頻率
　　原問題：圖中時刻點對應一頻率值，一個時刻點只有一個信號值，又怎么能得到他的頻率呢？
　　很好的問題。如文中所說，絕對意義的瞬時頻率其實是不存在的。單看一個時刻點的一個信號值，當然得不到它的頻率。我們只不過是用很短的一段信號的頻率作為該時刻的頻率，所以我們得到的只是時間分辨率有限的近似分析結果。這一想法在STFT上體現得很明顯。小波用衰減的基函數去測定信號的瞬時頻率，思想也類似。（不過到了Hilbert變換，思路就不一樣了，以后有機會細講）

4. 關于小波變換的不足
這要看和誰比了。
A.作為圖像處理方法，和多尺度幾何分析方法（超小波）比：
對于圖像這種二維信號的話，二維小波變換只能沿2個方向進行，對圖像中點的信息表達還可以，但是對線就比較差。而圖像中最重要的信息恰是那些邊緣線，這時候ridgelet（脊波）, curvelet（曲波）等多尺度幾何分析方法就更有優勢了。
B. 作為時頻分析方法，和希爾伯特-黃變換（HHT）比：
相比于HHT等時頻分析方法，小波依然沒脫離海森堡測不準原理的束縛，某種尺度下，不能在時間和頻率上同時具有很高的精度；以及小波是非適應性的，基函數選定了就不改了。

5. 關于文中表述的嚴謹性
評論中有不少朋友提到，我的一些表述不夠精準。這是肯定的，并且我也是知道的。比如傅里葉變換的理解部分，我所說的那種“乘出一個大的值”的表述肯定是不夠嚴謹的。具體我也在評論的回答中做了解釋。我想說的是通俗易懂和精確嚴謹實在難以兼得，如果要追求嚴謹，最好的就是教科書上的數學表達，它們無懈可擊，但是對于初學者來說，恐怕存在門檻。如果要通俗解釋，必然只能側重一個關鍵點，而出現漏洞。我想這也是教科書從來不把這些通俗解釋寫出來的原因吧——作者們不是不懂，而是怕寫錯。所以想深入理解傅里葉變換和小波變換的朋友還請認真學習教材，如果這篇文章能給一些初學者一點點幫助，我就心滿意足了。