排序算法系列：插入排序算法

概述

直接插入排序（Straight Insertion Sort）的基本操作是將一個記錄插入到已經排好序的有序表中，從而得到一個新的、記錄數增1的有序表。

　　　　　　　　　　　　　　　　　　　　　　　　　　　– 《大話數據結構》

---

版權說明

著作權歸作者所有。

商業轉載請聯系作者獲得授權，非商業轉載請注明出處。
本文作者：Coding-Naga
發表日期： 2016年3月24日
原文鏈接：http://blog.csdn.net/lemon_tree12138/article/details/50968422
來源：CSDN
很多其它內容：分類 >> 算法與數學

---

文件夾

• 概述
• 版權說明
• 文件夾
• 算法原理分析
• 算法步驟
• 邏輯實現
• 復雜度分析
• Ref
• Github源代碼下載

---

算法原理分析

從上面的概述中我們也就能夠知道了。這里對數組進行排序的過程須要兩個序列才干完畢。
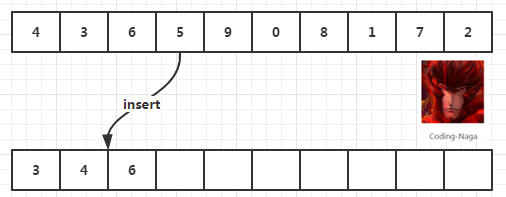
一個待排序的亂序序列。一個是已排序的有序序列。我們如今要要做的就是把亂序的元素一個一個地從亂序列中插入到有序序列中去。就像以下這樣：

但是，這里還是有一些不太好的地方，比較明顯地方就是我們須要額外加入一個輔助數組。

假設這個待排序數據比較大，那么可能加入輔助數組的策略就不能使用了。
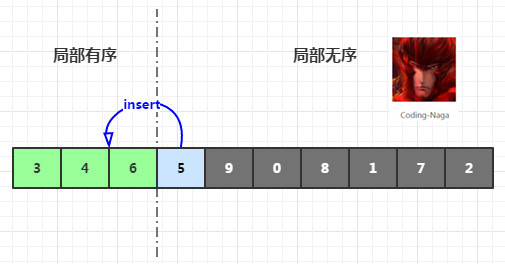
這里我們不難想到，在原始數組中。有這種一個等式：總體序列 = 有序序列 + 亂序序列
也就是說我們能夠把當前序列數組一分為二，左邊為有序，右邊為亂序。

這樣每次從亂序序列中取出第一個元素，從有序列中插入。直到序列總體有序為止。詳細的步驟請參見以下的算法步驟。

---

算法步驟

1. 默認序列中的第0個元素是有序的（由于僅僅有一個元素a[0]嘛，自然是有序的）。
2. 從下標為1（下標從0開始）的元素開始，取當前下標i位置處的元素a[i]保存到一個暫時變量waitInsert里。
3. 對前半部分有序序列的循環遍歷，并與waitInsert比較。直到遇到一個比waitInsert小的元素（這里默認是從小到大排序），此時的下標為j，那么如今僅僅要對a[j+1]進行賦值waitInsert就可以。
4. 將待插入元素的下標 i 向后推移一個位置。
5. 反復進行第2步到第4步。直到亂序序列中的元素被所有插入到有序序列中。
6. 經過以上5個步驟之后，總體序列必定有序。排序完畢。

---

邏輯實現

/** 排序算法的核心模塊* * @param array*      待排序數組*/private void sortCore(int[] array) {int arraySize = array.length;for (int i = 1; i < arraySize; i++) {int j = i;int waitInsert = array[i];while(j > 0 && waitInsert < array[j - 1]) {array[j] = array[j - 1];j--;}array[j] = waitInsert;}}

---

復雜度分析

排序方法	時間復雜度			空間復雜度	穩定性	復雜性
	平均情況	最壞情況	最好情況
插入排序	O(n2)	O(n2)	O(n)	O(n)	穩定	簡單

這里的最壞的情況和平均情況從代碼中就能夠看出來，由于有兩嵌套的for循環嘛。那么其最好的情況呢？這個就是對于一個有序的序列來說，不須要進行交換，僅僅是比較了n次，所以這里最好的時間復雜度就是O(n)。

---

Ref

• 《大話數據結構》

---

Github源代碼下載

https://github.com/William-Hai/ArraySortAlgorithm/blob/master/src/org/algorithm/array/sort/impl/InsertSort.java