cesium廣告牌

Description:

描述：

This is a standard dynamic programing problem of finding maximum profits with some constraints. This can be featured in any interview coding rounds.

這是在某些約束條件下找到最大利潤的標準動態編程問題。 這可以在任何采訪編碼回合中體現。

Problem statement:

問題陳述：

Consider a highway of M miles. The task is to place billboards on the highway such that revenue is maximized. The possible sites for billboards are given by number x₁ < x₂ < ... < x_(n-1) < x_n specifying positions in miles measured from one end of the road. If we place a billboard at position x_i, we receive a revenue of r_i > 0. The constraint is that no two billboards can be placed within t miles or less than it.

考慮一條M英里的高速公路。 任務是在高速公路上放置廣告牌，以使收入最大化。 廣告牌的可能位置由數字x ₁ <x ₂ <... <x _(n-1) <x _n給出，指定從道路的一端算起的英里位置。 如果將廣告牌放置在x _i位置，我們的收入r _i > 0 。 約束條件是在t英里以內或小于t英里內不能放置兩個廣告牌。

    Input:
M=15, n=5
x[n]= {6,8,12,14,15}
revenue[n] = {3,6,5,3,5}
t = 5
Output:
11

Explanation with example

舉例說明

So, we have to maximize the revenue by placing the billboards where the gap between any two billboard is t.

因此，我們必須通過將廣告牌放置在任意兩個廣告牌之間的距離為t的位置來最大化收入。

Here,

這里，

The corresponding distances of the billboards with respect to the origin are,

廣告牌相對于原點的相應距離為

    x[5]= {6,8,12,14,15}

We can augment the origin, so the augmented array becomes: (no need to augment if origin revenue exists)

我們可以擴充原點，因此擴充后的數組將變為：(如果存在原點收入，則無需擴充)

x[6]= {0,6,8,12,14,15}
t=5

The graphical interpretation of the billboards is like following:

廣告牌的圖形解釋如下：

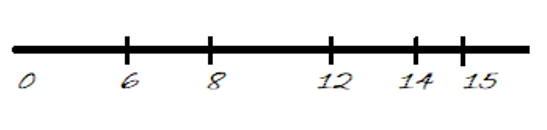
Figure 1: Billboards

圖1：廣告牌

The augmented revenue array:

擴充收益陣列：

    revenue[6] = {0,3,6,5,3,5}

Now, the brute force approach can be to check all the possible combination of billboards and updating the maximum revenue accumulated from each possible combinations.

現在，暴力破解方法可以是檢查廣告牌的所有可能組合，并更新每個可能組合所累積的最大收益。

Few of such possible combinations can be:

這樣的可能組合很少是：

So, maximum revenue that can be collected is 11.

因此，可以收取的最大收入為11 。

For any billboard b_i we have three choices

對于任何廣告牌b _我都有三種選擇

1. Don't pick b_i

   不要選擇_我

2. Start from b_i

   從_我開始

3. Pick b_i and other billboards accordingly

   相應地選擇b _i和其他廣告牌

Say,

說，

    M(i)=maximum revenue upto first i billboards

So,

所以，

    M(0)=0
if bi is not picked, M(i)=M(i-1)
if billboard placement starts from bi M(i)=r[i]
If we place bi then need to pace bj where d[i]>d[j]-t such that revenue maximizes
So,

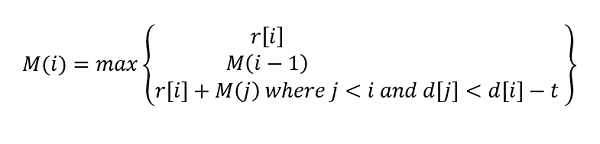
Problem Solution approach

問題解決方法

We convert the above recursion to dynamic programing as there will many overlapping sub problems solving the recursion. (Try to generate the recursion tree yourself)

我們將上述遞歸轉換為動態編程，因為將會有許多重疊的子問題解決遞歸。 (嘗試自己生成遞歸樹)

    1) Construct DP[n] for n billboards
// considering billboard placing starts from it
2) Fill the array with base value which is r[i] 
3) for  i=1 to n-1
// recursion case 1 and 2
// either not picking ith billboard or starting 
// from ith billboard which ever is maximum
dp[i] = max(dp[i-1],dp[i]);
// recursion case 3
// picking ith billboard
for j=0 to i-1
if(a[j]< a[i]-k)//feasible placing
dp[i]= max(dp[i],dp[j]+r[i]);
end for
end for
Result is dp[n-1]

C++ implementation:

C ++實現：

#include <bits/stdc++.h>
using namespace std;
int max(int x, int y)
{
return (x > y) ? x : y;
}
int billboard(vector<int> a, vector<int> r, int n, int k)
{
int dp[n];
for (int i = 0; i < n; i++)
dp[i] = r[i];
//base value
dp[0] = r[0];
for (int i = 1; i < n; i++) {
//first two recursion case
int mxn = max(dp[i - 1], dp[i]);
//picking ith billboard, third recursion case
for (int j = 0; j < i; j++) {
if (a[j] < a[i] - k)
mxn = max(mxn, dp[j] + r[i]);
}
dp[i] = mxn;
}
return dp[n - 1];
}
int main()
{
int n, k, item, m;
cout << "Enter highway length:\n";
cin >> m;
cout << "Enter number of billboards\n";
cin >> n;
cout << "Enter minimum distance between any two billboards\n";
cin >> k;
vector<int> a;
vector<int> r;
cout << "Enter billboard distances one by one from origin\n";
for (int i = 0; i < n; i++) {
cin >> item;
a.push_back(item);
}
cout << "Enter revenues for the respective billboards\n";
for (int i = 0; i < n; i++) {
cin >> item;
r.push_back(item);
}
if (a[0] == 0) {
a.insert(a.begin(), 0);
r.insert(r.begin(), 0);
n = n + 1;
}
cout << "Maximum revenue that can be collected is: " << billboard(a, r, n, k) << endl;
return 0;
}

Output

輸出量

RUN 1:
Enter highway length:
20
Enter number of billboards
5
Enter minimum distance between any two billboards
5
Enter billboard distances one by one from origin
3 7 12 13 14
Enter revenues for the respective billboards
15 10 1 6 2
Maximum revenue that can be collected is: 21
RUN 2:
Enter highway length:
15
Enter number of billboards
5
Enter minimum distance between any two billboards
5
Enter billboard distances one by one from origin
6 8 12 14 15
Enter revenues for the respective billboards
3 6 5 3 5
Maximum revenue that can be collected is: 11

翻譯自: https://www.includehelp.com/icp/highway-billboard.aspx

cesium廣告牌