事先說明：筆者初三，如在敘述中有不嚴謹的地方，還請諸位指出，自當感激不盡。

一.什么是斜坐標系

眾所周知，我們目前平面中使用相當廣的坐標系是笛卡爾發明的平面直角坐標系。然而，笛卡爾真的只使用了這一種坐標系嗎？顯然不是的。事實上，笛卡爾最先使用的是一種斜坐標系，即x軸與y軸夾角不為π/2的坐標系，這種坐標系更為一般化，也更自然。

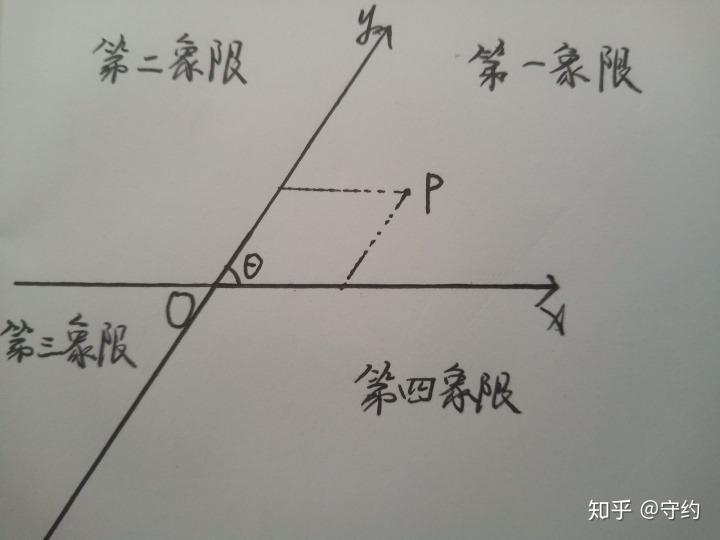
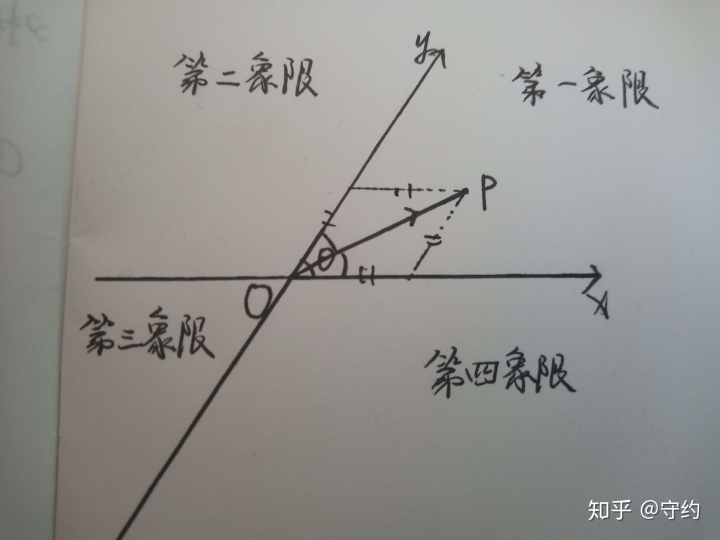
由此，對于一類題目如下：

△ABC平面內一動點p滿足向量Ap＝λ（向量AB/|向量AB|＋向量AC/|向量AC），我們根據斜坐標系可以直接看出它在∠BAC的角平分線上運動。

另附一些斜坐標系的小內容，感興趣的不妨自己推理一下：

1.與x軸垂直的直線，k＝-1/cosθ 2.與y軸垂直的直線，k＝-cosθ

3.若以三角形abc的a為原點，以兩邊方向為坐標軸方向建立平面斜角坐標系，（ab對應x軸，ac對應y軸）設Xb＝A，Yc＝B，則有：三角形垂心H（cosθ（B－Acosθ）/sin2θ，cosθ（A－Bcosθ）/sin2θ）外心Q（A-Bcosθ/2sin2θ，B－Acosθ/2sin2θ）于是有向量QH＝向量Qa＋向量Qb＋向量Qc（我才不會告訴你這是我證這個結論時作死不用垂心伴隨外接圓模型得到的）

4.規定同3，重心G（?a，?b）

5.設直線的傾斜角為α，則k＝sinα/sin（θ－α）

6.在斜坐標系內，若兩直線垂直且斜率存在，則滿足k1k2＋cosθ（k1+k2）=-1

二.斜坐標系內一些運算公式

1.兩點之間距離公式

首先，設向量AB＝（a，b）將向量AB坐標轉化為直角坐標系中坐標，則變成（a＋bcosθ，bsinθ）對此應用直角坐標系中向量模長公式，則有|AB|=√a2＋2abcosθ＋b2(sin2θ＋cos2θ）=√a2＋b2＋2abcosθ，這就是最終得到的距離公式了。

2.向量內積公式

同樣的套路，只要將向量AB變換成（a＋bcosθ，bsinθ），向量CD變換成（c＋dcosθ，dsinθ）那么向量AB·向量CD=ac＋bdcos2θ＋ad cosθ＋bc cosθ＋bdsin2θ＝（ac＋bd）＋cosθ（ad＋bc），即為所求

3.點到直線距離公式

這個我不能無腦搞了，那樣要算死人QAQ，請看圖：

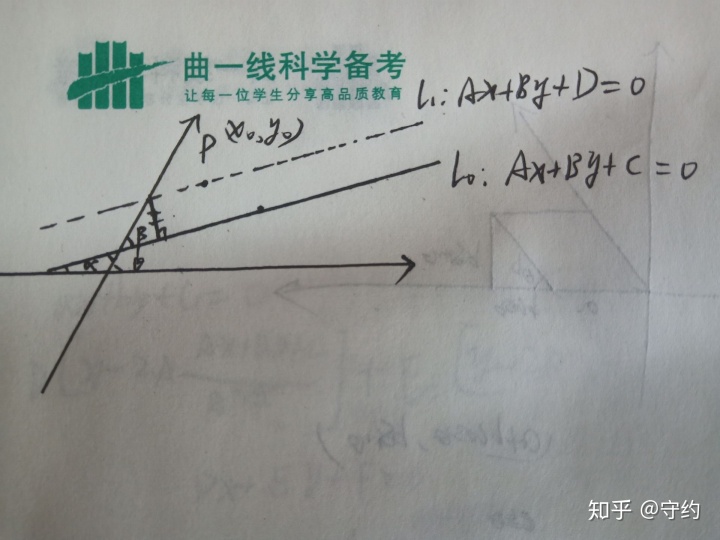
我們設點P（Xo，Yo），直線lo：Ax＋By＋C=0，過p做lo的平行線l1，那么點p到lo的距離轉化為l1與lo的距離。在l1與y軸交點處做lo的垂線。設角α，β，θ如圖。

先求l1，lo與y軸交點間長度：將x＝0代入，則有：

By1＋C＝0 ，y1＝-C/B

By2＋D＝0 ，y2＝-D/B

考慮到未知p的方位（可能在lo上方或下方），故線段l長度表示為|（C-D）/-B|，又因為有

AXo＋BYo＋D=0，則D＝-AXo-BYo，所以l長度為|（Ax0＋By0＋C）/-B|

觀察到我們所求的h＝|l|·sinβ＝|l|·sin（θ－α）＝|l|·（sinθcosα-sinαcosθ）

我們單獨研究α如圖：

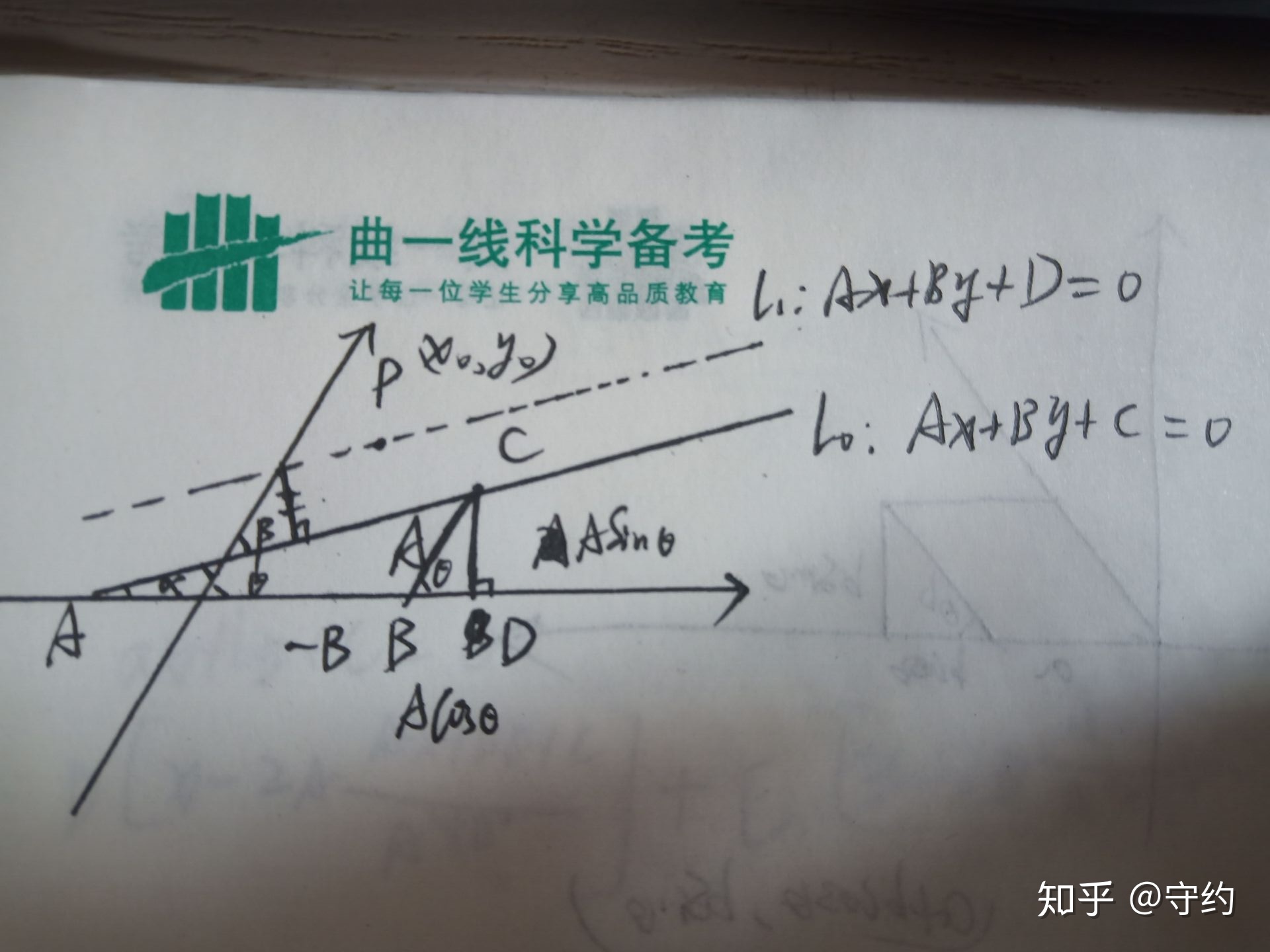
取lo上一點c，設它與x軸交點為a，并作cd⊥x軸，cb∥y軸，并且令向量ab=（-B，0），向量bc=（0，A），于是向量bd=（cosθ·A，0）向量dc＝（0，sinθ·A）那么在三角形acd中，可以解得ac＝√（cos2θ＋sin2θ）A2＋B2－2ABcosθ＝√A2＋B2－2ABcosθ，

故：sinα＝Asinθ/√A2＋B2－2ABcosθ

cosα=Acosθ-B/√A2＋B2－2ABcosθ

（正負性問題在此不做贅述了）

將得到的結果代入上式：

h=|（Ax0＋By0＋C）/-B|·[（Acosθ-B）sinθ－Asinθcosθ]/√A2＋B2－2ABcosθ

=|（Ax0＋By0＋C）/-B|·（-Bsinθ）/√A2＋B2－2ABcosθ，我們大膽地化簡，消去-B

得到h=|（Ax0＋By0＋C）|·sinθ/√A2＋B2－2ABcosθ，此時發現：

1.sinθ∈（0,1），即分式上方部分＞0

2.A2＋B2－2ABcosθ＞0，即分式下方部分＞0

這證明化簡正確。

綜上可得點到直線距離公式為：h=|（Ax0＋By0＋C）|·sinθ/√A2＋B2－2ABcosθ

4.等和線

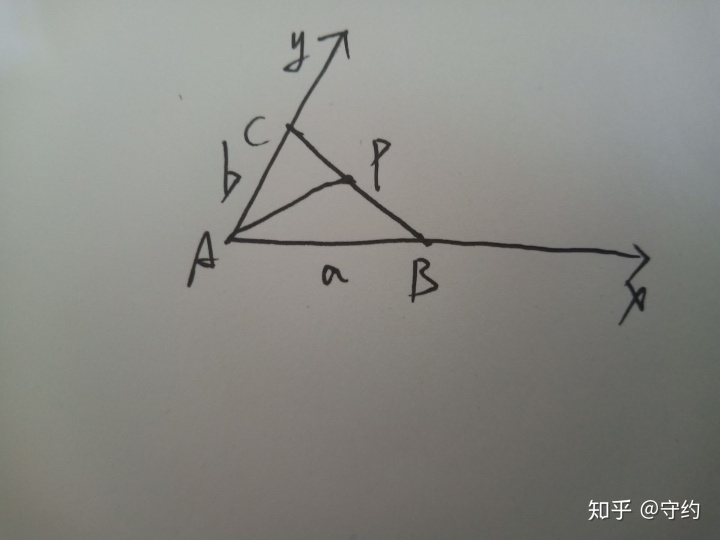
設|AB|=a，|AC|=b，P（ma，nb）

可解得lBC：y=-b/a·x＋b，變形為x/a＋y/b=1

∴ma/a＋nb/b=1，即m＋n＝1，得證。同樣易構“等差線”。

5.奔馳定理

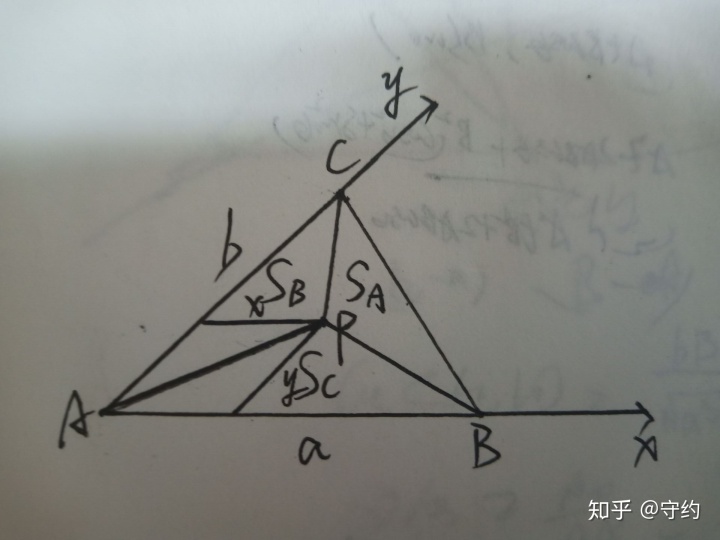
設B（a，0）C（0，b）P（x,y）S△ABC=S，則：

SB=x/a ·S，向量BP=（x-a，y）

Sc=y/b ·S，向量CP=（x，y-b）

SA=（1－x/a-y/b）S，向量AP=（x，y）

∴向量AP·SA+向量BP·SB+向量CP·SC=（（x-x2/a-xy/b＋x2/a-x＋xy/b）·S，（y-xy/a-y2/b＋xy/a+y2/b-y）·S）=0向量，得證。

利用斜坐標系，我們也可以得到p在△ABC外的情況，過程類似不再贅述，結論是：在△ABP、△ACP、△BCP中，圖形除了與AB邊（或BC邊、AC邊）有交點外與三角形ABC再無交集的，在前面加上負號，則等式依然成立。

下面附一道例題：

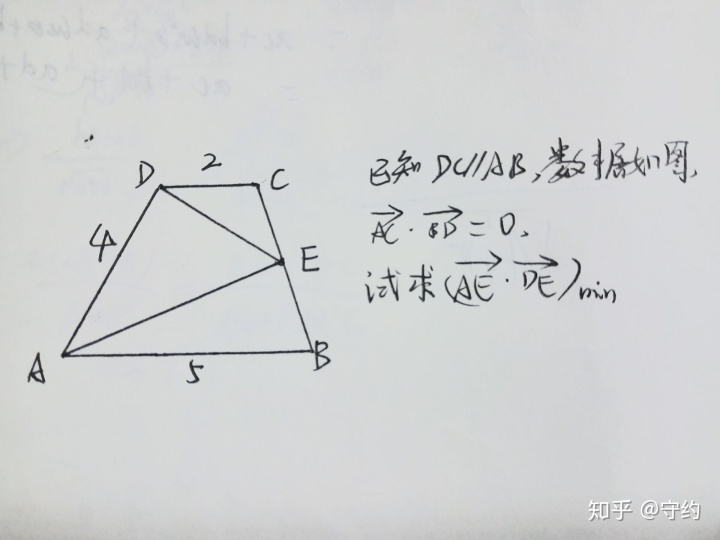
解：以AB為x軸，AD為y軸建立斜坐標系

則有C（2，4）B（5，0）D（0，4）lCB：y=-4/3x+20/3，即4x+3y-20=0

∴（2，4）·（-5，4）=0

∴-10+16-12cosθ=0，得θ＝π/3

由極化恒等式，取AD中點F，則向量AE·向量DE=EF2-AF2

由點到直線距離公式得：EF2min=（7·根號3）2/（16+9-12）=147/13

∴（向量AE·向量DE）min=147/13 -4=95/13