之前在公司組內分享了紅黑樹的工作原理，今天把它整理下發出來，希望能對大家有所幫助，對自己也算是一個知識點的總結。

這篇文章算是我寫博客寫公眾號以來畫圖最多的一篇文章了，沒有之一，我希望盡可能多地用圖片來形象地描述紅黑樹的各種操作的前后變換原理，幫助大家來理解紅黑樹的工作原理，下面，多圖預警開始了。

在講紅黑樹之前，我們首先來了解下下面幾個概念：二叉樹，排序二叉樹以及平衡二叉樹。

二叉樹

二叉樹指的是每個節點最多只能有兩個字數的有序樹。通常左邊的子樹稱為左子樹 ，右邊的子樹稱為右子樹 。這里說的有序樹強調的是二叉樹的左子樹和右子樹的次序不能隨意顛倒。

二叉樹簡單的示意圖如下：

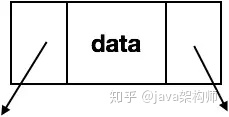
代碼定義：

class Node {T data;Node left;Node right;
}

排序二叉樹

所謂排序二叉樹，顧名思義，排序二叉樹是有順序的，它是一種特殊結構的二叉樹，我們可以對樹中所有節點進行排序和檢索。

性質

• 若它的左子樹不空，則左子樹上所有節點的值均小于它的根節點的值；
• 若她的右子樹不空，則右子樹上所有節點的值均大于它的根節點的值；
• 具有遞歸性，排序二叉樹的左子樹、右子樹也是排序二叉樹。

排序二叉樹簡單示意圖：

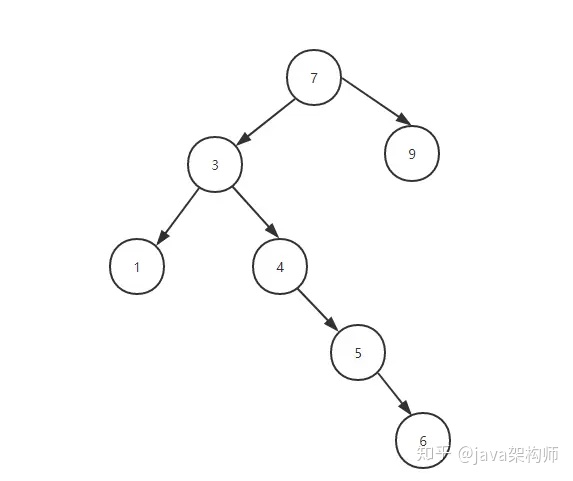
排序二叉樹退化成鏈表

排序二叉樹的左子樹上所有節點的值小于根節點的值，右子樹上所有節點的值大于根節點的值，當我們插入一組元素正好是有序的時候，這時會讓排序二叉樹退化成鏈表。

正常情況下，排序二叉樹是如下圖這樣的：

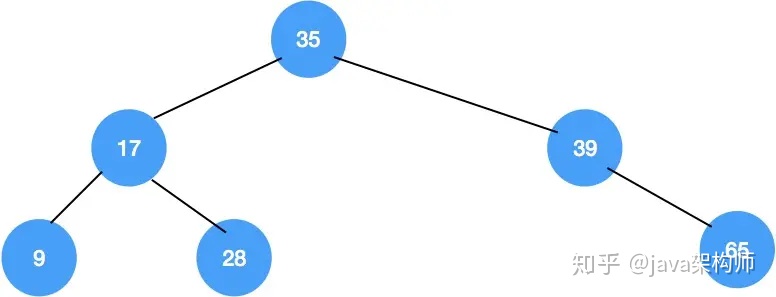
但是，當插入的一組元素正好是有序的時候，排序二叉樹就變成了下邊這樣了，就變成了普通的鏈表結構，如下圖所示:

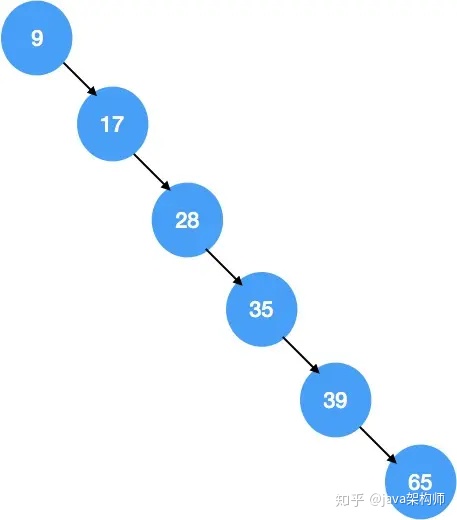
正常情況下的排序二叉樹檢索效率類似于二分查找，二分查找的時間復雜度為 O(log n)，但是如果排序二叉樹退化成鏈表結構，那么檢索效率就變成了線性的 O(n) 的，這樣相對于 O(log n) 來說，檢索效率肯定是要差不少的。

思考，二分查找和正常的排序二叉樹的時間復雜度都是 O(log n)，那么為什么是O(log n) ？

關于 O(log n) 的分析下面這篇文章講解的非常好，感興趣的可以看下這篇文章 二分查找的時間復雜度.md)，文章是拿二分查找來舉例的，二分查找和平衡二叉樹的時間復雜度是一樣的，理解了二分查找的時間復雜度，再來理解平衡二叉樹就不難了，這里就不贅述了。

繼續回到我們的主題上，為了解決排序二叉樹在特殊情況下會退化成鏈表的問題（鏈表的檢索效率是 O(n) 相對正常二叉樹來說要差不少），所以有人發明了平衡二叉樹和紅黑樹類似的平衡樹。

平衡二叉樹

平衡二叉數又被稱為 AVL 樹，AVL 樹的名字來源于它的發明作者 G.M. Adelson-Velsky 和 E.M. Landis，取自兩人名字的首字母。

官方定義：它或者是一顆空樹，或者具有以下性質的排序二叉樹：它的左子樹和右子樹的深度之差(平衡因子)的絕對值不超過1，且它的左子樹和右子樹都是一顆平衡二叉樹。

兩個條件：

• 平衡二叉樹必須是排序二叉樹，也就是說平衡二叉樹他的左子樹所有節點的值必須小于根節點的值，它的右子樹上所有節點的值必須大于它的根節點的值。
• 左子樹和右子樹的深度之差的絕對值不超過1。

紅黑樹

講了這么多概念，接下來主角紅黑樹終于要上場了。

為什么有紅黑樹？

其實紅黑樹和上面的平衡二叉樹類似，本質上都是為了解決排序二叉樹在極端情況下退化成鏈表導致檢索效率大大降低的問題，紅黑樹最早是由 Rudolf Bayer 于 1972 年發明的。

紅黑樹首先肯定是一個排序二叉樹，它在每個節點上增加了一個存儲位來表示節點的顏色，可以是 RED 或 BLACK 。

Java 中實現紅黑樹大概結構圖如下所示：

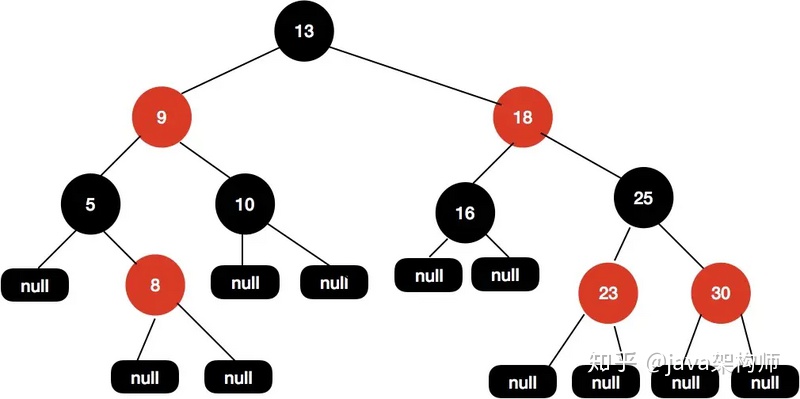
紅黑樹的特性

• 性質1：每個節點要么是紅色，要么是黑色。
• 性質2：根節點永遠是黑色的。
• 性質3：所有的葉子節點都是空節點（即null），并且是黑色的。
• 性質4：每個紅色節點的兩個子節點都是黑色。（從每個葉子到根的路徑上不會有兩個連續的紅色節點。）
• 性質5：從任一節點到其子樹中每個葉子節點的路徑都包含相同數量的黑色節點。

針對上面的 5 種性質，我們簡單理解下，對于性質 1 和性質 2 ，相當于是對紅黑樹每個節點的約束，根節點是黑色，其他的節點要么是紅色，要么是黑色。

對于性質 3 中指定紅黑樹的每個葉子節點都是空節點，而且葉子節點都是黑色，但 Java 實現的紅黑樹會使用 null 來代表空節點，因此我們在遍歷 Java里的紅黑樹的時候會看不到葉子節點，而看到的是每個葉子節點都是紅色的，這一點需要注意。

對于性質 5，這里我們需要注意的是，這里的描述是從任一節點，從任一節點到它的子樹的每個葉子節點黑色節點的數量都是相同的，這個數量被稱為這個節點的黑高。

如果我們從根節點出發到每個葉子節點的路徑都包含相同數量的黑色節點，這個黑色節點的數量被稱為樹的黑色高度。樹的黑色高度和節點的黑色高度是不一樣的，這里要注意區分。

其實到這里有人可能會問了，紅黑樹的性質說了一大堆，那是不是說只要保證紅黑樹的節點是紅黑交替就能保證樹是平衡的呢？

其實不是這樣的，我們可以看來看下面這張圖：

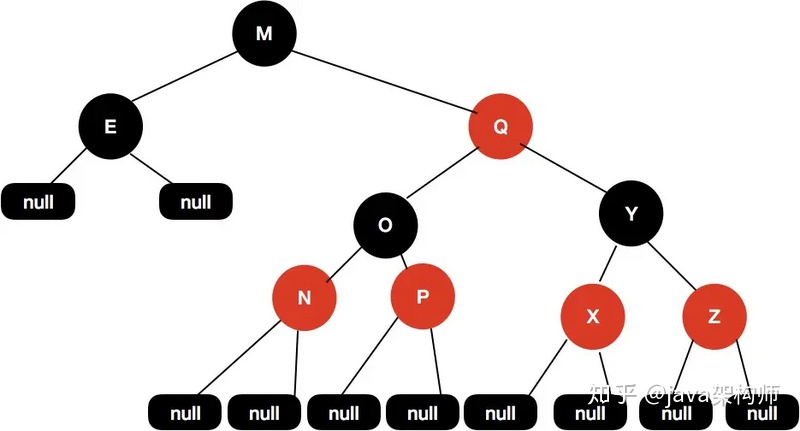
左邊的子樹都是黑色節點，但是這個紅黑樹依然是平衡的，5 條性質它都滿足。

這個樹的黑色高度為 3，從根節點到葉子節點的最短路徑長度是 2，該路徑上全是黑色節點，包括葉子節點，從根節點到葉子節點最長路徑為 4，每個黑色節點之間會插入紅色節點。

通過上面的性質 4 和性質 5，其實上保證了沒有任何一條路徑會比其他路徑長出兩倍，所以這樣的紅黑樹是平衡的。

其實這算是一個推論，紅黑樹在最差情況下，最長的路徑都不會比最短的路徑長出兩倍。其實紅黑樹并不是真正的平衡二叉樹，它只能保證大致是平衡的，因為紅黑樹的高度不會無限增高，在實際應用用，紅黑樹的統計性能要高于平衡二叉樹，但極端性能略差。

紅黑樹的插入

想要徹底理解紅黑樹，除了上面說到的理解紅黑樹的性質以外，就是理解紅黑樹的插入操作了。

紅黑樹的插入和普通排序二叉樹的插入基本一致，排序二叉樹的要求是左子樹上的所有節點都要比根節點小，右子樹上的所有節點都要比跟節點大，當插入一個新的節點的時候，首先要找到當前要插入的節點適合放在排序二叉樹哪個位置，然后插入當前節點即可。紅黑樹和排序二叉樹不同的是，紅黑樹需要在插入節點調整樹的結構來讓樹保持平衡。

一般情況下，紅黑樹中新插入的節點都是紅色的，那么，為什么說新加入到紅黑樹中的節點要是紅色的呢？

這個問題可以這樣理解，我們從性質5中知道，當前紅黑樹中從根節點到每個葉子節點的黑色節點數量是一樣的，此時假如新的黑色節點的話，必然破壞規則，但加入紅色節點卻不一定，除非其父節點就是紅色節點，因此加入紅色節點，破壞規則的可能性小一些。

接下來我們重點來講紅黑樹插入新節點后是如何保持平衡的。

給定下面這樣一顆紅黑樹：

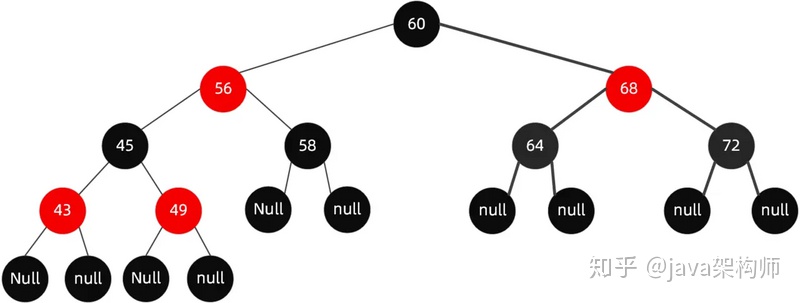
當我們插入值為66的節點的時候，示意圖如下：

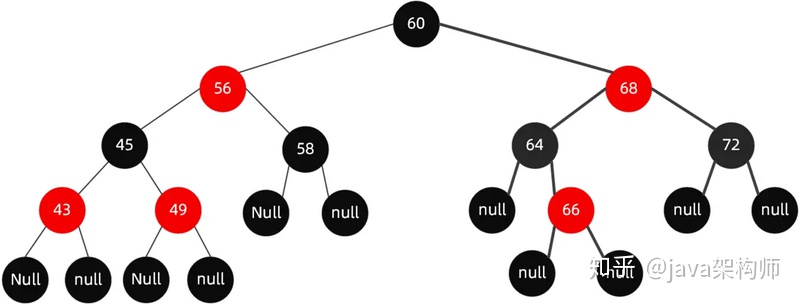
很明顯，這個時候結構依然遵循著上述5大特性，無需啟動自動平衡機制調整節點平衡狀態。

如果再向里面插入值為51的節點呢，這個時候紅黑樹變成了這樣。

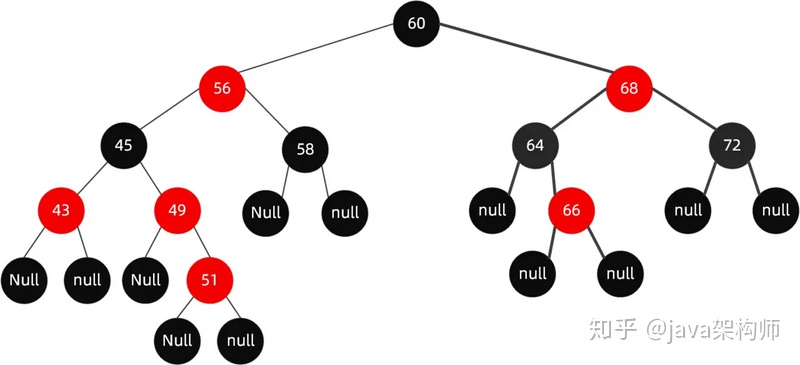
這樣的結構實際上是不滿足性質4的，紅色兩個子節點必須是黑色的，而這里49這個紅色節點現在有個51的紅色節點與其相連。

這個時候我們需要調整這個樹的結構來保證紅黑樹的平衡。

首先嘗試將49這個節點設置為黑色，如下示意圖。

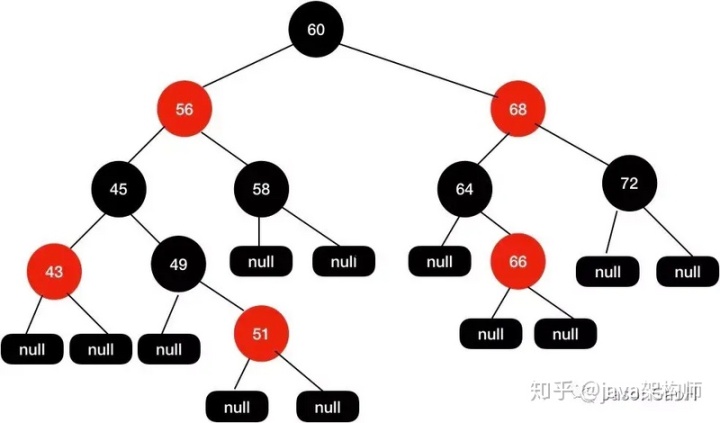
這個時候我們發現黑高是不對的，其中 60-56-45-49-51-null 這條路徑有 4 個黑節點，其他路徑的黑色節點是 3 個。

接著調整紅黑樹，我們再次嘗試把45這個節點設置為紅色的，如下圖所示：

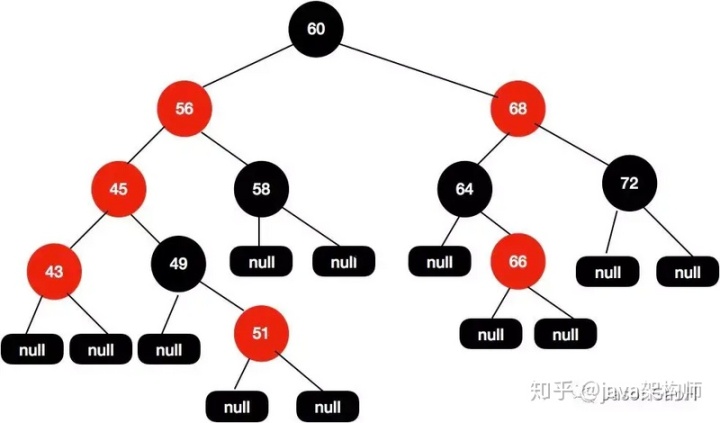
這個時候我們發現問題又來了，56-45-43 都是紅色節點的，出現了紅色節點相連的問題。

于是我們需要再把 56 和 43 設置為黑色的，如下圖所示。

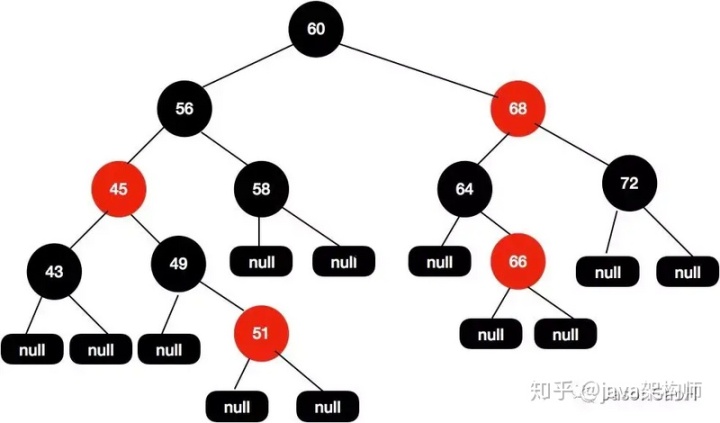
于是我們把 68 這個紅色節點設置為黑色的。

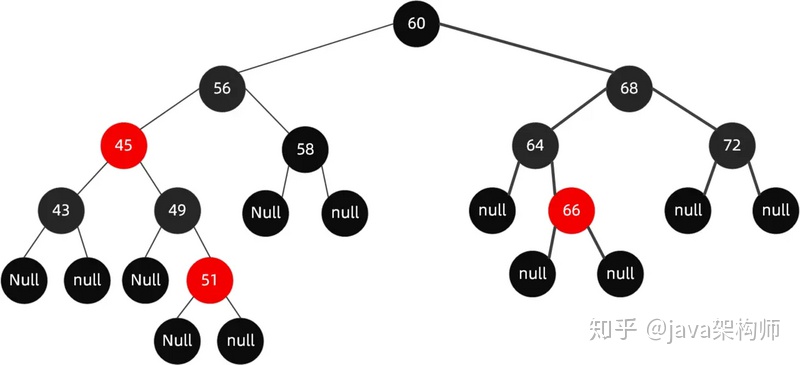
對于這種紅黑樹插入節點的情況下，我們可以只需要通過變色就可以保持樹的平衡了。但是并不是每次都是這么幸運的，當變色行不通的時候，我們需要考慮另一個手段就是旋轉了。

例如下面這種情況，同樣還是拿這顆紅黑樹舉例。

現在這顆紅黑樹，我們現在插入節點65。

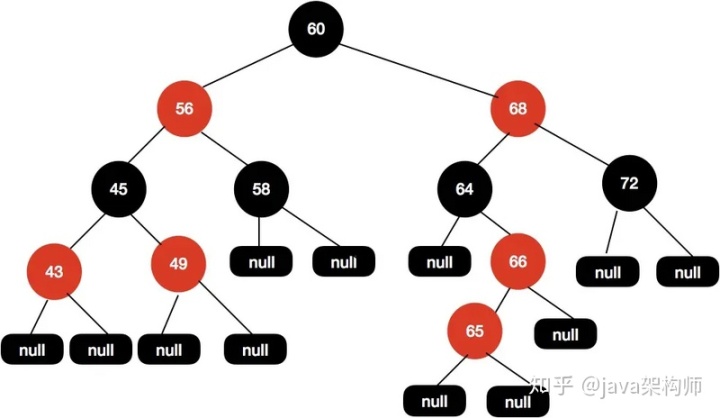
我們嘗試把 66 這個節點設置為黑色，如下圖所示。

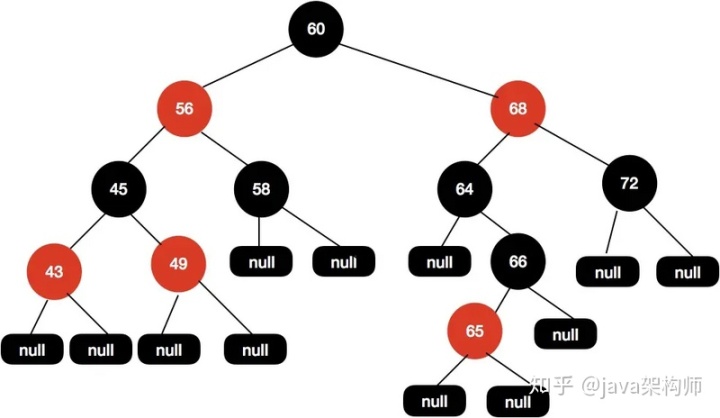
這樣操作之后黑高又出現不一致的情況了，60-68-64-null 有 3 個黑色節點，而60-68-64-66-null 這條路徑有 4 個黑色節點，這樣的結構是不平衡的。

或者我們把 68 設置為黑色，把 64 設置為紅色，如下圖所示：

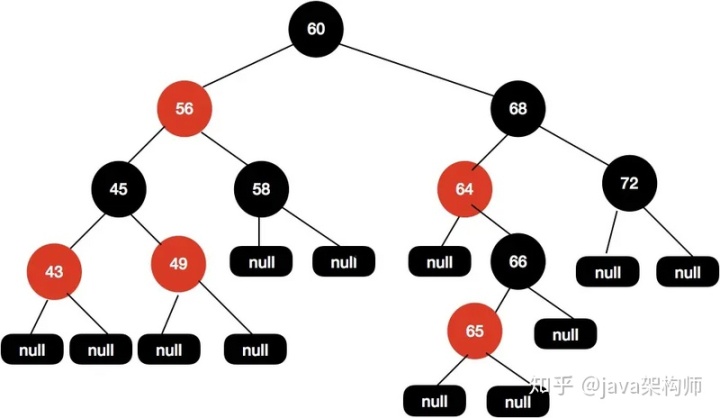
但是，同樣的問題，上面這顆紅黑樹的黑色高度還是不一致，60-68-64-null 和 60-68-64-66-null 這兩條路徑黑色高度還是不一致。

這種情況如果只通過變色的情況是不能保持紅黑樹的平衡的。

紅黑樹的旋轉

接下來我們講講紅黑樹的旋轉，旋轉分為左旋和右旋。

左旋

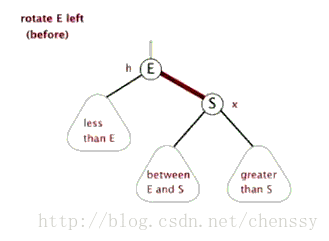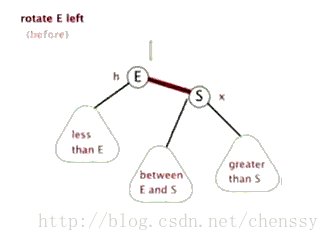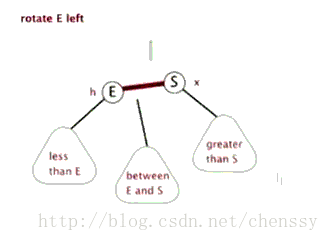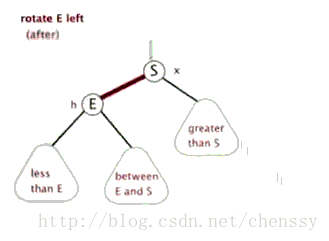
文字描述：逆時針旋轉兩個節點，讓一個節點被其右子節點取代，而該節點成為右子節點的左子節點。

文字描述太抽象，接下來看下圖片展示。

首先斷開節點PL與右子節點G的關系，同時將其右子節點的引用指向節點C2；然后斷開節點G與左子節點C2的關系，同時將G的左子節點的應用指向節點PL。

接下來再放下 gif 圖，希望能幫助大家更好地理解左旋，圖片來自網絡。

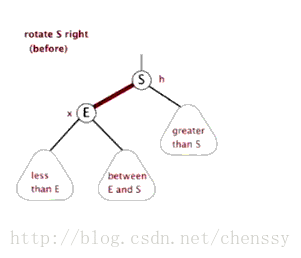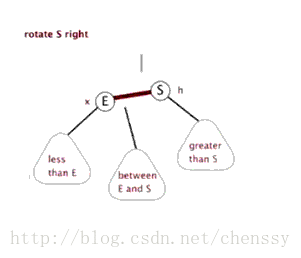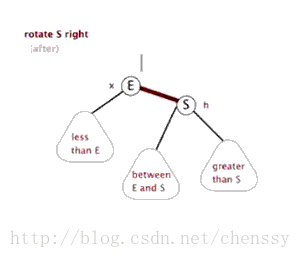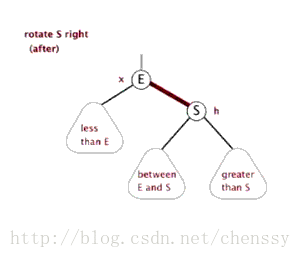
右旋

文字描述：順時針旋轉兩個節點，讓一個節點被其左子節點取代，而該節點成為左子節點的右子節點。

右旋的圖片展示：

首先斷開節點G與左子節點PL的關系，同時將其左子節點的引用指向節點C2；然后斷開節點PL與右子節點C2的關系，同時將PL的右子節點的應用指向節點G。

右旋的gif展示（圖片來自網絡）:

介紹完了左旋和右旋基本操作，我們來詳細介紹下紅黑樹的幾種旋轉場景。

左左節點旋轉（插入節點的父節點是左節點，插入節點也是左節點）

如下圖所示的紅黑樹，我們插入節點是65。

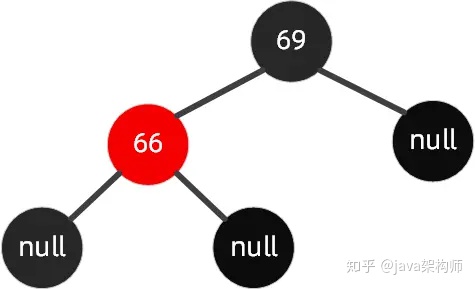
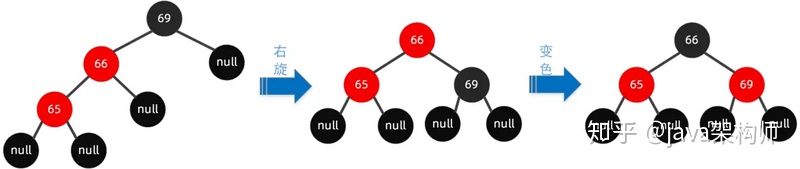
操作步驟如下可以圍繞祖父節點 69 右旋，再結合變色，步驟如下所示：

左右節點旋轉（插入節點的父節點是左節點，插入節點是右節點）

還是上面這顆紅黑樹，我們再插入節點 67。

這種情況我們可以這樣操作，先圍繞父節點 66 左旋，然后再圍繞祖父節點 69 右旋，最后再將 67 設置為黑色，把 69 設置為紅色，如下圖所示。

右左節點旋轉（插入節點的父節點是右節點，插入節點左節點）

如下圖這種情況，我們要插入節點68。

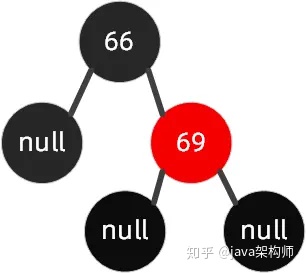
這種情況，我們可以先圍繞父節點 69 右旋，接著再圍繞祖父節點 66 左旋，最后把 68 節點設置為黑色，把 66 設置為紅色，我們的具體操作步驟如下所示。

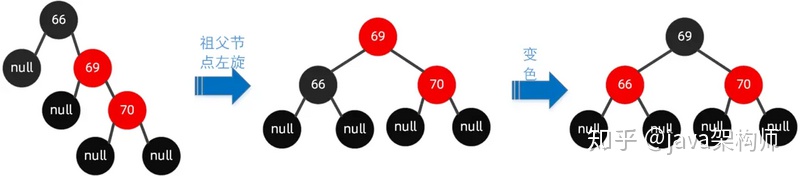
右右節點旋轉（插入節點的父節點是右節點，插入節點也是右節點）

還是來上面的圖來舉例，我們在這顆紅黑樹上插入節點 70 。

我們可以這樣操作圍繞祖父節點 66 左旋，再把旋轉后的根節點 69 設置為黑色，把 66 這個節點設置為紅色。具體可以參看下圖：

紅黑樹在 Java 中的實現

Java 中的紅黑樹實現類是 TreeMap ，接下來我們嘗試從源碼角度來逐行解釋 TreeMap 這一套機制是如何運作的。

// TreeMap中使用Entry來描述每個節點static final class Entry<K,V> implements Map.Entry<K,V> {K key;V value;Entry<K,V> left;Entry<K,V> right;Entry<K,V> parent;boolean color = BLACK;...}
復制代碼

TreeMap 的put方法。

public V put(K key, V value) {//先以t保存鏈表的root節點Entry<K,V> t = root;//如果t=null,表明是一個空鏈表，即該TreeMap里沒有任何Entry作為rootif (t == null) {compare(key, key); // type (and possibly null) check//將新的key-value創建一個Entry，并將該Entry作為rootroot = new Entry<>(key, value, null);size = 1;//記錄修改次數加1modCount++;return null;}int cmp;Entry<K,V> parent;// split comparator and comparable pathsComparator<? super K> cpr = comparator;//如果比較器cpr不為null，即表明采用定制排序if (cpr != null) {do {//使用parent上次循環后的t所引用的Entryparent = t;//將新插入的key和t的key進行比較cmp = cpr.compare(key, t.key);//如果新插入的key小于t的key，t等于t的左邊節點if (cmp < 0)t = t.left;//如果新插入的key大于t的key，t等于t的右邊節點    else if (cmp > 0)t = t.right;else//如果兩個key相等，新value覆蓋原有的value，并返回原有的valuereturn t.setValue(value);} while (t != null);}else {if (key == null)throw new NullPointerException();@SuppressWarnings("unchecked")Comparable<? super K> k = (Comparable<? super K>) key;do {parent = t;cmp = k.compareTo(t.key);if (cmp < 0)t = t.left;else if (cmp > 0)t = t.right;elsereturn t.setValue(value);} while (t != null);}//將新插入的節點作為parent節點的子節點Entry<K,V> e = new Entry<>(key, value, parent);//如果新插入key小于parent的key,則e作為parent的左子節點if (cmp < 0)parent.left = e;//如果新插入key小于parent的key，則e作為parent的右子節點elseparent.right = e;//修復紅黑樹fixAfterInsertion(e);size++;modCount++;return null;}
復制代碼
//插入節點后修復紅黑樹
private void fixAfterInsertion(Entry<K,V> x) {x.color = RED;//直到x節點的父節點不是根，且x的父節點是紅色while (x != null && x != root && x.parent.color == RED) {//如果x的父節點是其父節點的左子節點if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {//獲取x的父節點的兄弟節點Entry<K,V> y = rightOf(parentOf(parentOf(x)));//如果x的父節點的兄弟節點是紅色if (colorOf(y) == RED) {     //將x的父節點設置為黑色setColor(parentOf(x), BLACK);//將x的父節點的兄弟節點設置為黑色setColor(y, BLACK);//將x的父節點的父節點設為紅色setColor(parentOf(parentOf(x)), RED);x = parentOf(parentOf(x));}//如果x的父節點的兄弟節點是黑色else {   //TODO 對應情況第二種，左右節點旋轉//如果x是其父節點的右子節點if (x == rightOf(parentOf(x))) {//將x的父節點設為xx = parentOf(x);//右旋轉rotateLeft(x);}//把x的父節點設置為黑色setColor(parentOf(x), BLACK);//把x的父節點父節點設為紅色setColor(parentOf(parentOf(x)), RED);rotateRight(parentOf(parentOf(x)));}}//如果x的父節點是其父節點的右子節點else {//獲取x的父節點的兄弟節點Entry<K,V> y = leftOf(parentOf(parentOf(x)));//只著色的情況對應的是最開始例子，沒有旋轉操作，但是要對應多次變換//如果x的父節點的兄弟節點是紅色  if (colorOf(y) == RED) {//將x的父節點設置為黑色setColor(parentOf(x), BLACK);//將x的父節點的兄弟節點設為黑色setColor(y, BLACK);//將X的父節點的父節點（G）設置紅色setColor(parentOf(parentOf(x)), RED);//將x設為x的父節點的節點x = parentOf(parentOf(x));}//如果x的父節點的兄弟節點是黑色else {//如果x是其父節點的左子節點if (x == leftOf(parentOf(x))) {//將x的父節點設為xx = parentOf(x);//右旋轉rotateRight(x);}//將x的父節點設為黑色setColor(parentOf(x), BLACK);//把x的父節點的父節點設為紅色setColor(parentOf(parentOf(x)), RED);rotateLeft(parentOf(parentOf(x)));}}}//將根節點強制設置為黑色root.color = BLACK;
}
復制代碼

TreeMap的插入節點和普通的排序二叉樹沒啥區別，唯一不同的是，在TreeMap 插入節點后會調用方法fixAfterInsertion(e)來重新調整紅黑樹的結構來讓紅黑樹保持平衡。

我們重點關注下紅黑樹的fixAfterInsertion(e)方法，接下來我們來分別介紹兩種場景來演示fixAfterInsertion(e)方法的執行流程。

第一種場景：只需變色即可平衡

同樣是拿這顆紅黑樹舉例，現在我們插入節點 51。

當我們需要插入節點51的時候，這個時候TreeMap 的 put 方法執行后會得到下面這張圖。

接著調用fixAfterInsertion(e)方法，如下代碼流程所示。

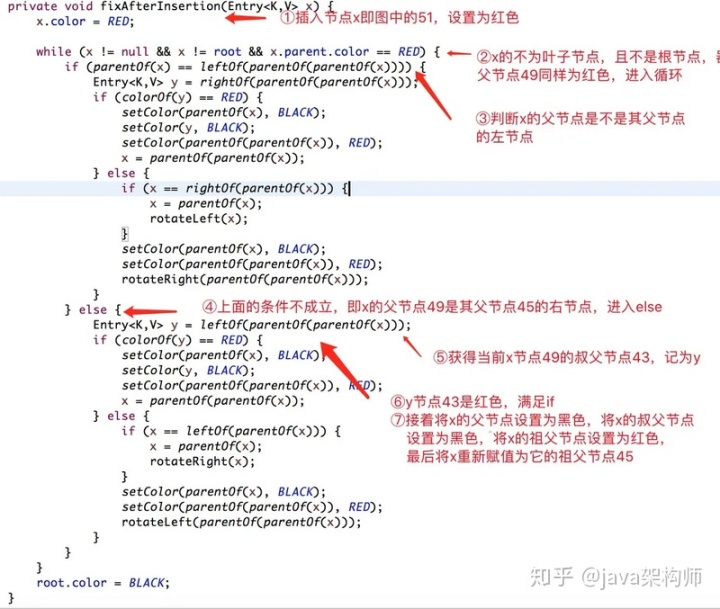
當第一次進入循環后，執行后會得到下面的紅黑樹結構。

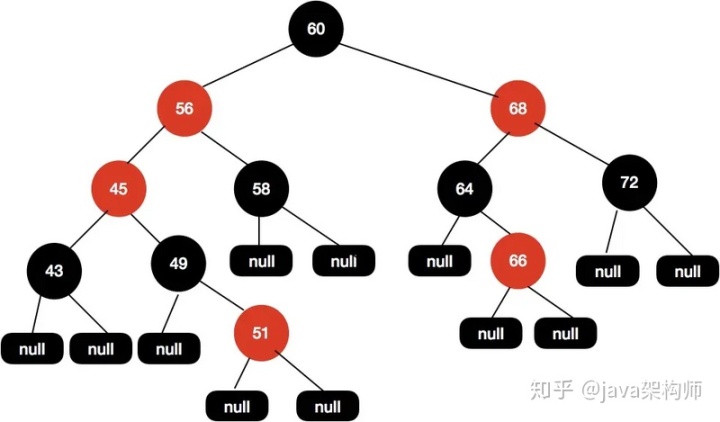
在把 x 重新賦值后，重新進入 while 循環，此時的 x 節點為 45 。

執行上述流程后，得到下面所示的紅黑樹結構。

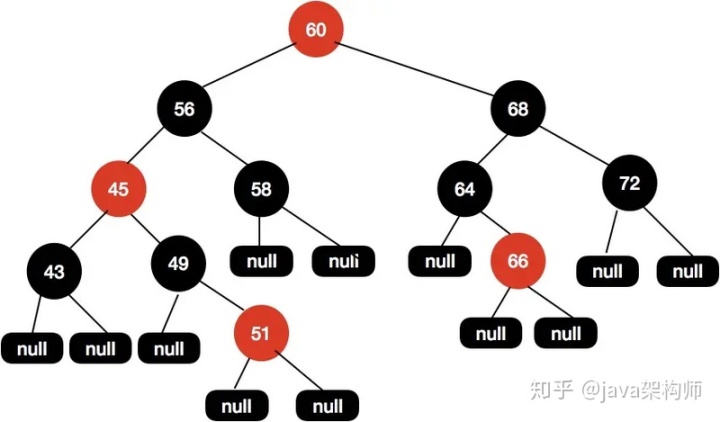
這個時候x被重新賦值為60，因為60是根節點，所以會退出 while 循環。在退出循序后，會再次把根節點設置為黑色，得到最終的結構如下圖所示。

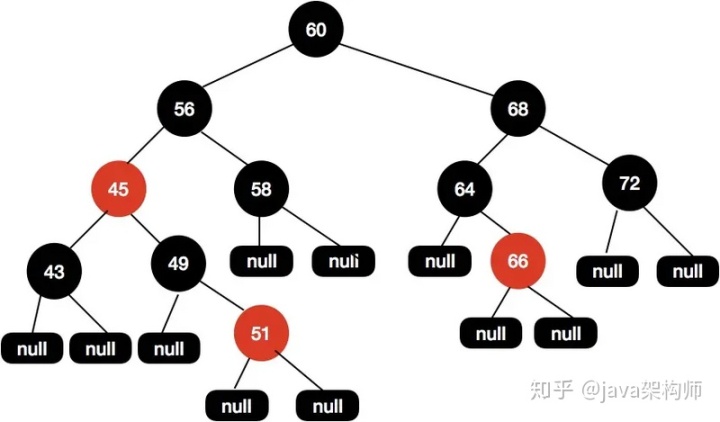
最后經過兩次執行while循環后，我們的紅黑樹會調整成現在這樣的結構，這樣的紅黑樹結構是平衡的，所以路徑的黑高一致，并且沒有紅色節點相連的情況。

第二種場景 旋轉搭配變色來保持平衡

接下來我們再來演示第二種場景，需要結合變色和旋轉一起來保持平衡。

給定下面這樣一顆紅黑樹：

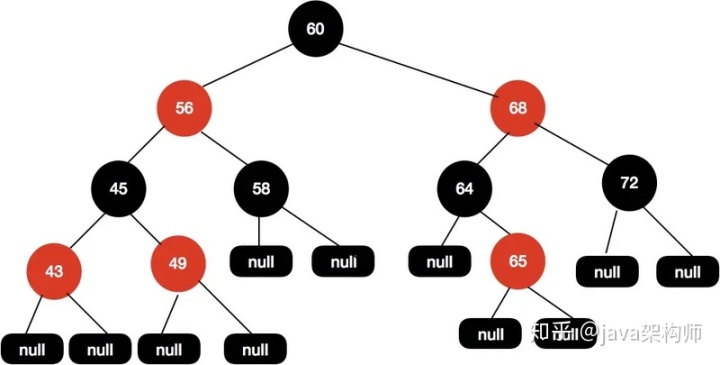
現在我們插入節點66，得到如下樹結構。

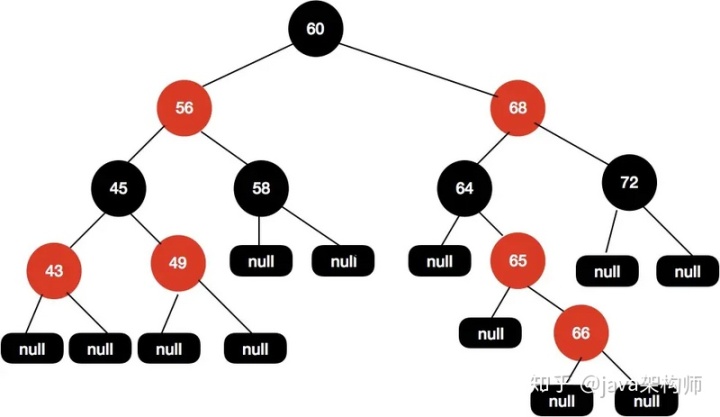
同樣地，我們進入fixAfterInsertion(e)方法。

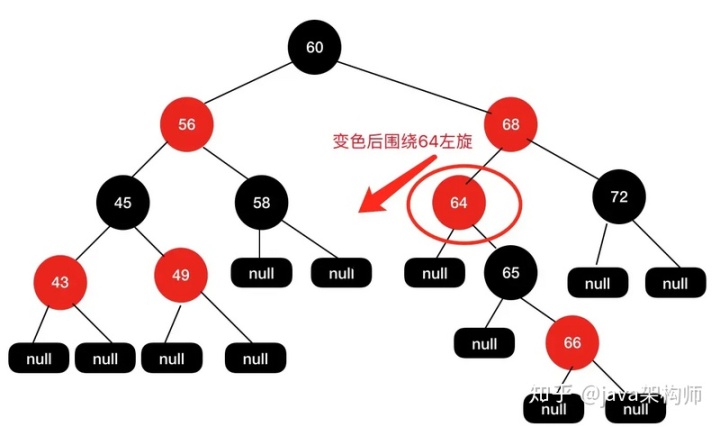
最終我們得到的紅黑樹結構如下圖所示：

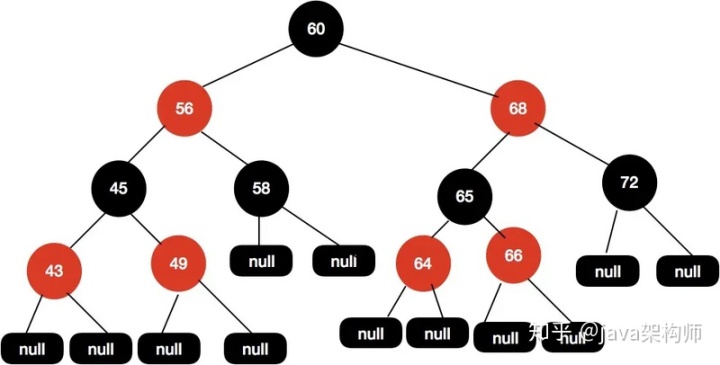
調整成這樣的結構我們的紅黑樹又再次保持平衡了。

演示 TreeMap 的流程就拿這兩種場景舉例了，其他的就不一一舉例了。

紅黑樹的刪除

因為之前的分享只整理了紅黑樹的插入部分，本來想著紅黑樹的刪除就不整理了，有人跟我反饋說紅黑樹的刪除相對更復雜，于是索性還是把紅黑樹的刪除再整理下。

刪除相對插入來說，的確是要復雜一點，但是復雜的地方是因為在刪除節點的這個操作情況有很多種，但是插入不一樣，插入節點的時候實際上這個節點的位置是確定的，在節點插入成功后只需要調整紅黑樹的平衡就可以了。

但是刪除不一樣的是，刪除節點的時候我們不能簡單地把這個節點設置為null，因為如果這個節點有子節點的情況下，不能簡單地把當前刪除的節點設置為null，這個被刪除的節點的位置需要有新的節點來填補。這樣一來，需要分多種情況來處理了。

刪除節點是根節點

直接刪除根節點即可。

刪掉節點的左子節點和右子節點都是為空

直接刪除當前節點即可。

刪除節點有一個子節點不為空

這個時候需要使用子節點來代替當前需要刪除的節點，然后再把子節點刪除即可。

給定下面這棵樹，當我們需要刪除節點69的時候。

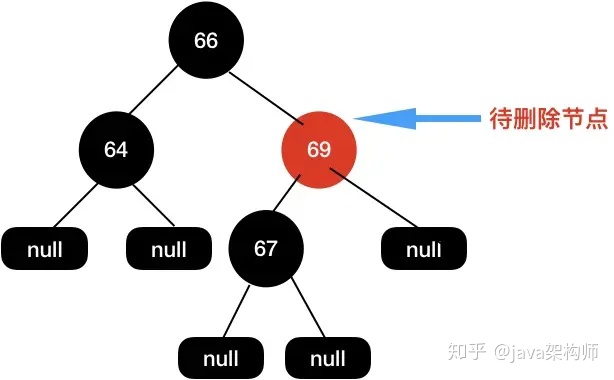
首先用子節點代替當前待刪除節點，然后再把子節點刪除。

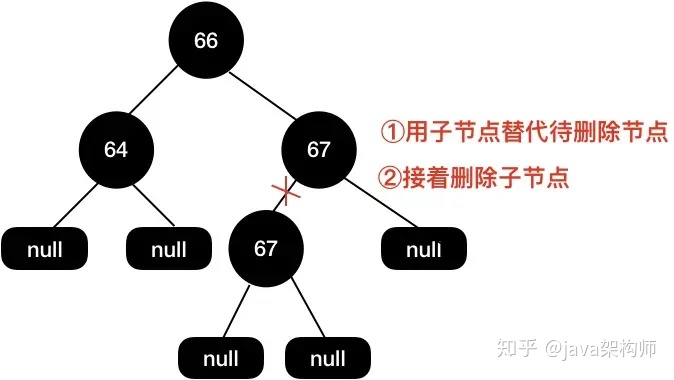
最終的紅黑樹結構如下面所示，這個結構的紅黑樹我們是不需要通過變色+旋轉來保持紅黑樹的平衡了，因為將子節點刪除后樹已經是平衡的了。

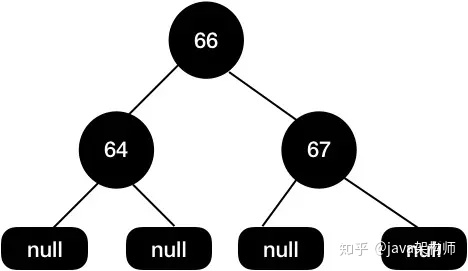
還有一種場景是當我們待刪除節點是黑色的，黑色的節點被刪除后，樹的黑高就會出現不一致的情況，這個時候就需要重新調整結構。

還是拿上面這顆刪除節點后的紅黑樹舉例，我們現在需要刪除節點67。

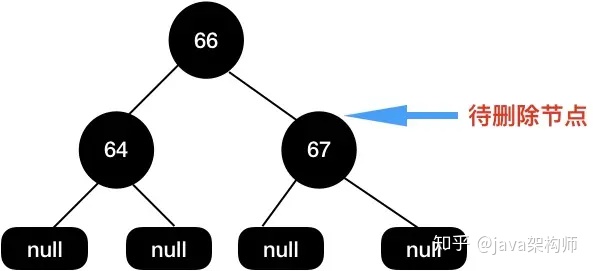
因為67 這個節點的兩個子節點都是null，所以直接刪除,得到如下圖所示結構：

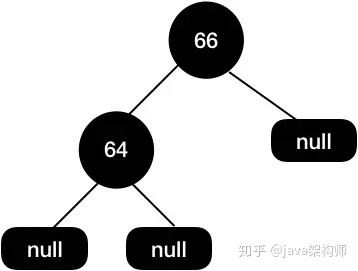
這個時候我們樹的黑高是不一致的，左邊黑高是3，右邊是2，所以我們需要把64節點設置為紅色來保持平衡。

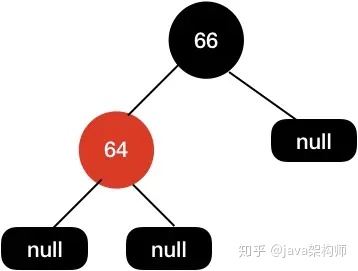
刪除節點兩個子節點都不為空

刪除節點兩個子節點都不為空的情況下，跟上面有一個節點不為空的情況下也是有點類似，同樣是需要找能替代當前節點的節點，找到后，把能替代刪除節點值復制過來，然后再把替代節點刪除掉。

• 先找到替代節點，也就是前驅節點或者后繼節點
• 然后把前驅節點或者后繼節點復制到當前待刪除節點的位置，然后在刪除前驅節點或者后繼節點。

那么什么叫做前驅，什么叫做后繼呢？ 前驅是左子樹中最大的節點，后繼則是右子樹中最小的節點。

前驅或者后繼都是最接近當前節點的節點，當我們需要刪除當前節點的時候，也就是找到能替代當前節點的節點，能夠替代當前節點肯定是最接近當前節點。

在當前刪除節點兩個子節點不為空的場景下，我們需要再進行細分，主要分為以下三種情況。

第一種，前驅節點為黑色節點，同時有一個非空節點

如下面這樣一棵樹，我們需要刪除節點64：

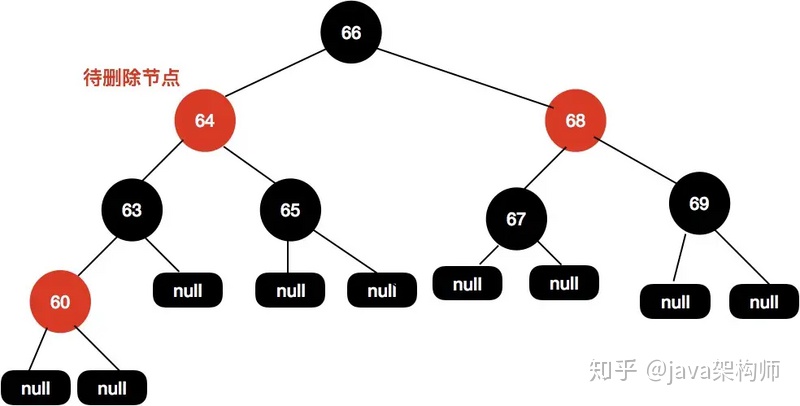
首先找到前驅節點，把前驅節點復制到當前節點：

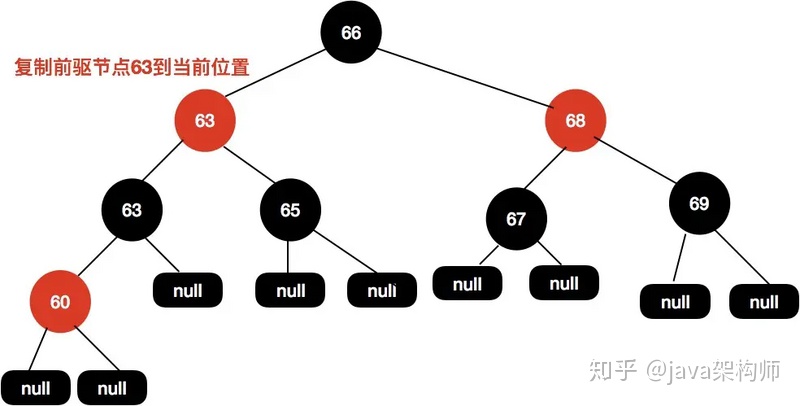
接著刪除前驅節點。

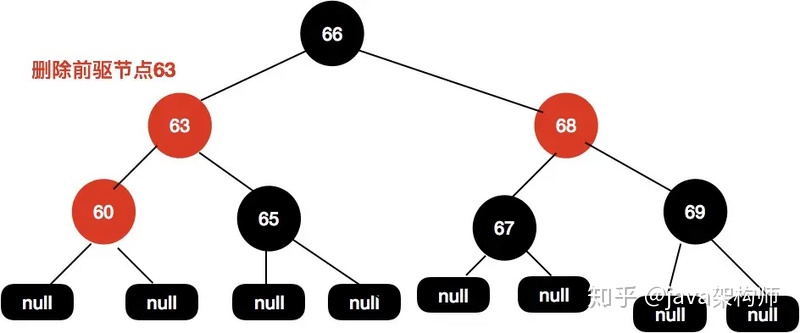
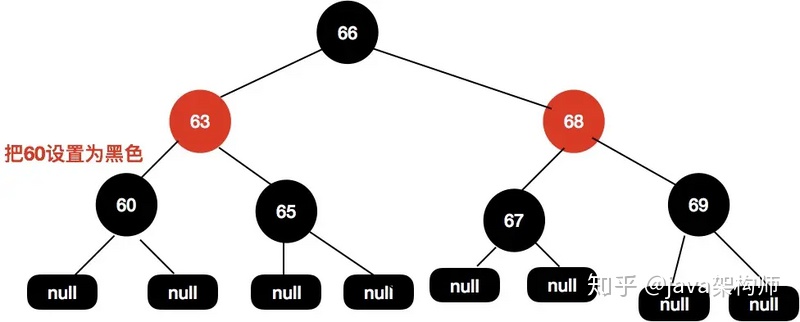
這個時候63和60這個節點都是紅色的，我們嘗試把60這個節點設置為紅色即可使整個紅黑樹達到平衡。

第二種，前驅節點為黑色節點，同時子節點都為空

前驅節點是黑色的，子節點都為空，這個時候操作步驟與上面基本類似。

如下操作步驟：

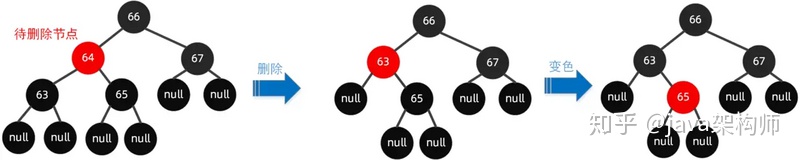
因為要刪除節點64，接著找到前驅節點63，把63節點復制到當前位置，然后將前驅節點63刪除掉，變色后出現黑高不一致的情況下，最后把63節點設置為黑色，把65節點設置為紅色，這樣就能保證紅黑樹的平衡。

第三種，前驅節點為紅色節點，同時子節點都為空

給定下面這顆紅黑樹，我們需要刪除節點64的時候。

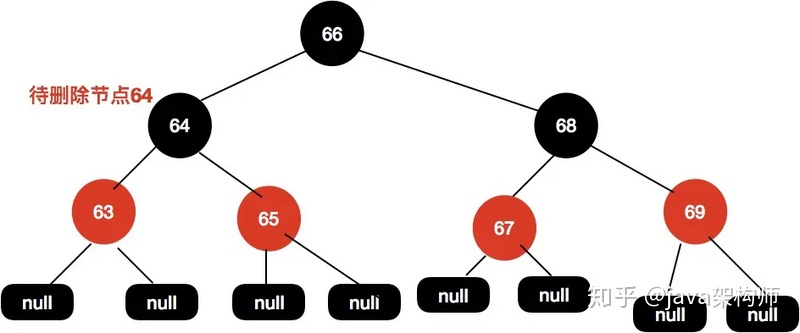
同樣地，我們找到64的前驅節點63，接著把63賦值到64這個位置。

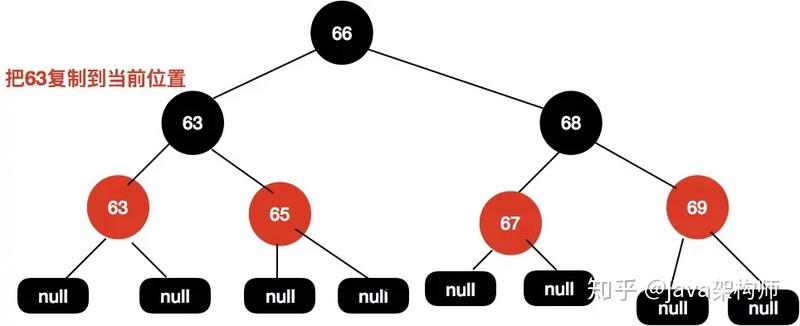
然后刪除前驅節點。

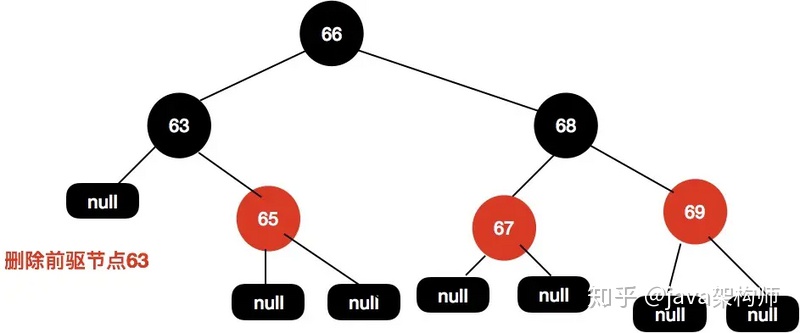
刪除節點后不需要變色也不需要旋轉即可保持樹的平衡。

終于把紅黑樹的基本原理部分寫完了，用了很多示意圖，這篇文章是在之前分享的 ppt 上再整理出來，我覺得自己應該算是把基本操作講明白了，整理這篇文章前前后后用了近一周左右，因為平時上班，基本上只有周末有時間才有時間整理，如有問題請留言討論。

如果您覺得寫得還可以，請您幫忙點個贊，您的點贊真的是對我最大的支持，也是我能繼續寫下去的動力，感謝。

轉自：https://juejin.im/post/5df4aa...

怒求一波贊

能堅持看到這兒的都是努力學習的人，我們相信，努力奮斗終將會使我們過上自己想要的生活。

我會努力更新原創干貨，也會收集一些精品文章，供大家日常學習。不論如何，如果大家覺得在我這兒能學到點東西，在這兒厚著臉皮的向大家求個贊，求個關注，求個分享。我一定不會辜負大家，為大家的學習之路添加更多精彩的文章。

創作不易，堅持不易，大家的支持是我最大的動力，再次謝謝大家。

下面這篇文章，是我收集的5000G的精品VIP視頻的部分目錄，都是會免費分享給大家的，大家可以點進去看看是否有自己需要的，如果沒有，大家也可以通過公眾號或者微信私聊我，我也會盡力去收集。