DAY 5.

• DAY 5.
  • 1.羅爾定理
  • 2.拉格朗日定理
  • 3.柯西中值定理
  • 4.泰勒公式及麥克勞林公式

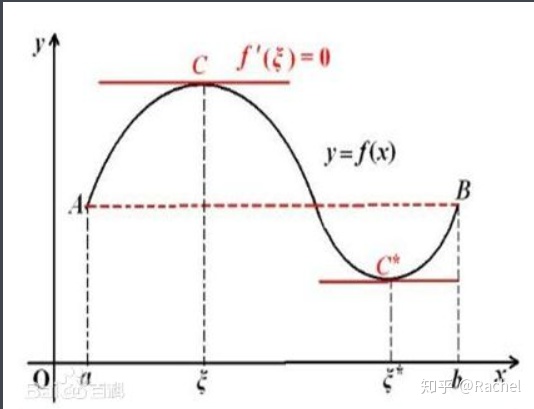
1.羅爾定理

羅爾定理描述如下：

如果 R 上的函數 f(x) 滿足以下條件：（1）在閉區間 [a,b] 上連續，（2）在開區間 (a,b) 內可導，（3）f(a)=f(b)，則至少存在一個 ξ∈(a,b)，使得 f'(ξ)=0。

例題1

若方程

有一個正根，

，試證方程

必有一個小于

正根。

解：

令

因為原方程有一個

的正根，所以有

= 0

而：

由羅爾定理可知:必存在一

使得

所以

當

時原式證畢

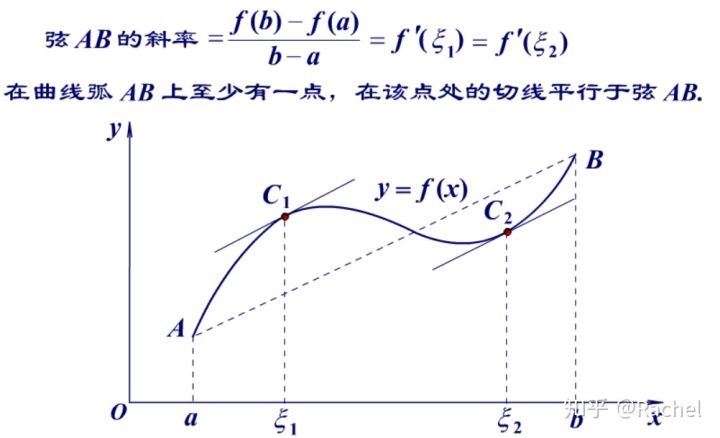
2.拉格朗日定理

拉格朗日定理其實是羅爾定理的一種推廣

如果函數

滿足：1) 在閉區間[a,b]上連續；2) 在開區間(a,b)內可導；那么在(a,b)內至少有一點$xi(a<xi

例題2

設 a > b >0, n>1 證明$nb^{n-1}(a-b) < a^n - b^n

解： 設

由拉格朗日定理可得：

=

因為：

所以

且 n > 1

可得：

3.柯西中值定理

柯西中值定理是前兩者的進一步推廣，期末不常考，因為用柯西定理證明的題，用羅爾和拉格朗日都可以證明出來

柯西定理就是當我們把拉格朗日定理里面的

看成

,

看成

獲得兩個參數方程

得到：

例題3

設 b>a>0 若

在【a,b】上連續，在（a,b）上可導，求證

使得

解：

設

由柯西中值定理可知：

證畢

4.泰勒公式及麥克勞林公式

當泰勒公式其中的

的時候就變成了麥克勞林公式

有兩個余項：

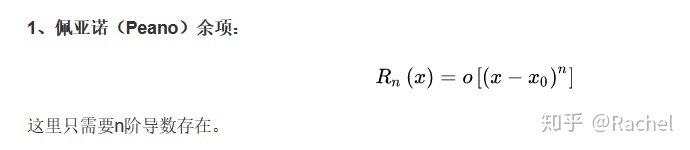
要記住一些常用函數的泰勒公式
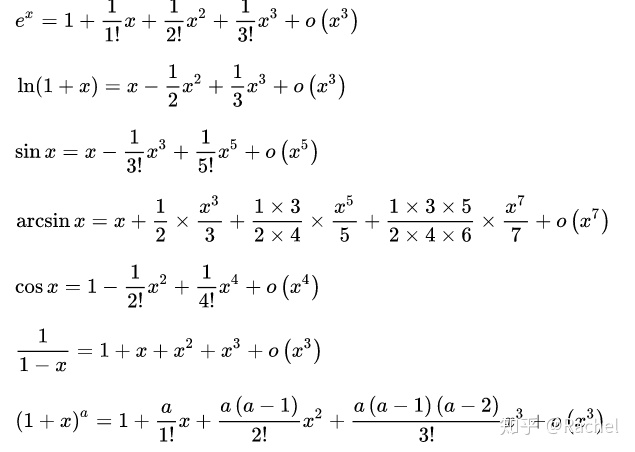