最近完成的一個項目用到了SVM,之前也一直有聽說支持向量機,知道它是機器學習中一種非常厲害的算法。利用將近一個星期的時間學習了一下支持向量機,把原理推了一遍,感覺支持向量機確實挺厲害的,尤其是核函數變換可以把一個低維不可分問題轉化為高維可分的問題。
需要解決的問題
支持向量機是一種監督學習的方法,主要用來進行分類和回歸分析,當我們對一些數據進行分類的時候,可能會考慮以下問題:
- 怎么選擇決策邊界?什么樣的決策邊界最好?
- 目標函數如何求解?
- 對于線性不可分的問題該用何種方法來解決。
解決問題流程
- 選取決策邊界(選取出最好的決策邊界)
- 列目標函數
- 優化目標函數
- 求解優化目標(利用拉格朗日乘子法)
- 軟間隔問題的解決(解決離群點)
- 核函數變換
決策邊界的選擇
Step1
當我們拿到一些簡單的線性可分的數據的時候,如下圖,將兩類數據分類的決策邊界有n條直線(圖中顯示了三條),那么哪一個決策邊界才是最好的呢。
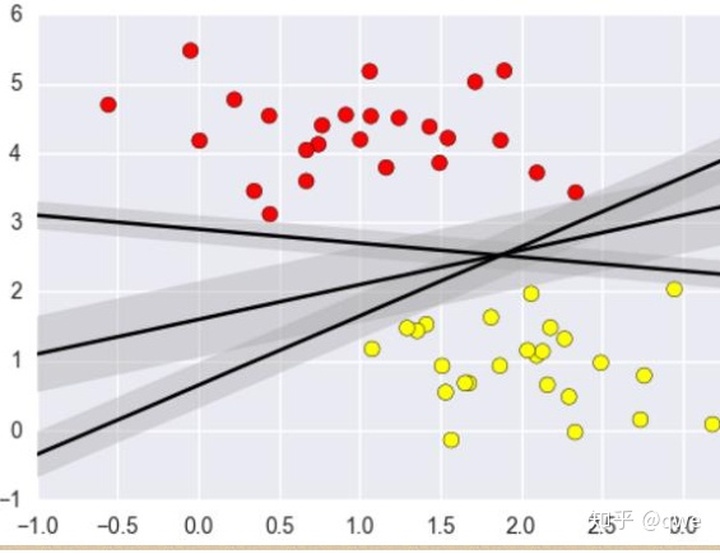
直覺告訴我:中間的那一條邊界是最好的,而實際也的確如此:
舉個簡單的栗子:
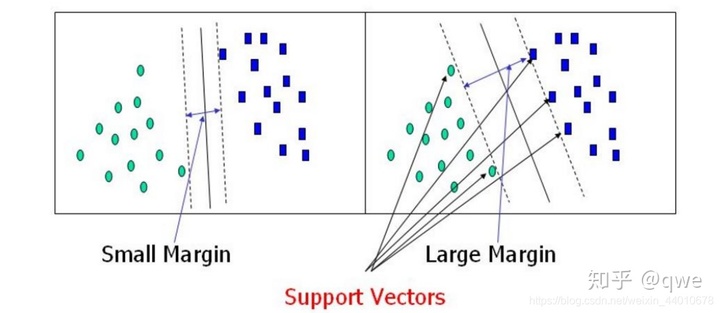
兩側的數據就好比是兩邊是河,我們肯定希望可以走的地方越寬越好,這樣掉入河里的幾率就降低了。
所以我們選擇的決策邊界是:選出來離河岸最遠的(河岸就是邊界上的點,要Large Margin),第二個肯定比第一個效果好。
好了,知道要選擇什么樣的邊界之后,接下來就是要求解邊界了。
我們希望找到離決策邊界最近的點,這樣就找到了決策邊界。
所以,假設決策邊界是一個陰影平面,求點到平面的距離轉換成點到點的距離,然后再垂直方向上的投影。大概的模型如下圖:
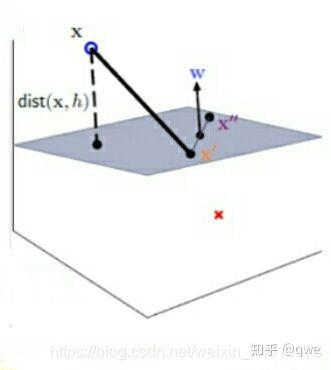
x為一個點,面的方程可以用線性方程來描述:
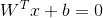
其中w為法向量,決定了超平面的方向,b為位移量,決定了超平面與原點的距離。(學過高數幾何那一部分的應該都看的懂)
接下來就是算一下x到平面的距離。假設平面上有兩點x’,x’’,那么則有:
W^Tx'+b=0WTx′+b=0
W^Tx''+b=0WTx′′+b=0
即W^T(x''-x')+b=0WT(x′′?x′)+b=0
直接求垂線的距離比較難,但是我們可以通過求xx’兩點的長度,再求其在垂直方向的投影來得到垂線的距離。
通過計算可以得到以下式子:
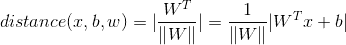
Step 2
接下來我們引入數據來將上面的式子完整化具體化
假設現在有數據集(x1,y1),(x2,y2)……(xn,yn)(x為數據,y為標簽)。
在這里我們認為當X為正例時Y=1,負例是Y=-1。
這里的±1僅僅是一個標號,代表正負樣本,并不是具體的數值,主要是因為這里是二分類,而且方便下面的簡化。和Logistics Regression(Logistics Regression中用0和1來區分正負例)一樣,而且這是可以由Logistics Regression推出來的(具體過程不在這里寫了)
假設現在的決策邊界為:
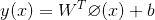
如果感覺?(x)這種表述方式不太習慣,可以考慮所有的?(x)=x,式主要是為了強調,在實際問題中,輸入空間x一般不會作為模型的輸入,而是要將輸入空間通過一定的特征轉換算法?(x),轉換到特征空間,最后在特征空間中做算法學習。而且,在實際問題中,各種算法基本上都是死的,但是,特征變換的這個過程?(x)卻是活的,很多時候,決定一個實際問題能不能很好的解決,?(x)起著決定性的作用。舉個簡單的例子,比如Logistics Regression,數據最好要做歸一化,如果數據不歸一化,那么那些方差特別大的特征就會成為主特征,影響模型的計算,?(x)就可以做這個事情。
給上面這個函數做一個定義:當預測的結果大于0的時候Y=1(對應著正例),小于0的時候為負例。即:
y(x)大于0時,y_iyi?=1,y(x)小于0時,y_iyi?=-1,那么下面我們可以將這個式子合著寫成y_iyi?y(x)>0。
Step 3
對于第一步推出來的點到距離的公式,我們注意到有絕對值的存在,在計算機中這是不容易表示的,于是我們可以引入第二步的yi,因為y_iyi?y(x)>0。所以我們可以將距離公式表達成:
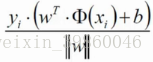
這樣一來就去掉了絕對值。
優化目標
優化目標:找到一條線,使得距離線最近的點能夠最遠(找到一條線,使得距離河岸最近的線能夠最遠)
即:
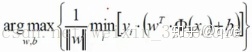
首先min中求了所有點中離線最近的點,max是使得該點與邊界最遠。
這個目標看起來是不是特別繁瑣~那接下來我們再來簡化一下。
通過一個放縮變換:決策方程中的(w,b)可以通過放縮使其結果值|Y|≥1(之前認為是大于0,現在嚴格了一些)。
這個放縮的過程就是通過等比例擴大或縮小y,w,b的系數,總能得到|Y|≥1。而且表達式中重要的不是w 和 b 的取值,重要的是 w 和 b 的比值, w 和 b 的比值決定了一個決策面的點集,也就決定了一個決策面。
|Y|≥1,即:
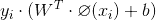
所以上面優化目標中
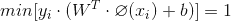
所以我們現在只剩下:
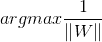
只需要將1/||W||最大化就OK了。所以這就是我們的目標函數。
目標函數求解
由上面的推導我們可以知道,目標函數為:
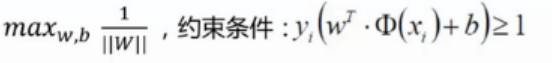
求解這個式子就是求解一個極大值,機器中一般都是將求極大值的問題轉化為求極小值的問題。求1/W的極大值不就是求W的極小值嘛。所以我們可以轉化成:
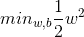
這個式子也不好求啊~那么該如何求解呢?
這里就要用到拉格朗日乘子法:
我們需要解決的問題是帶約束的拉格朗日乘子法問題:

是不是有點復雜……總之吧,我們要求得式子可以轉化為:
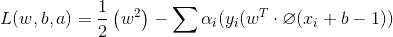
還有約束:
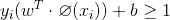
咦,這個α是什么東東,現在我們先理解為每個xi前面加了個系數,下面會繼續說,我們可以把求w轉為求α。
SVM求解推導
Step 1
接下來的推導我感覺挺復雜的……推完想吐。
引入數學KKT公式(這里不詳細證明)
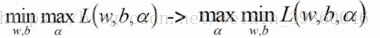
大概意思就是先求里面的最大值在求外面的最小值和先求里面的最小值在求外面的最大值是一樣的。
求極小值肯定先想到的就是求偏導,分別對w和b求偏導,讓偏導等于0:
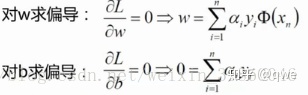
再將得到的結果帶到我們所要求解的原式中:
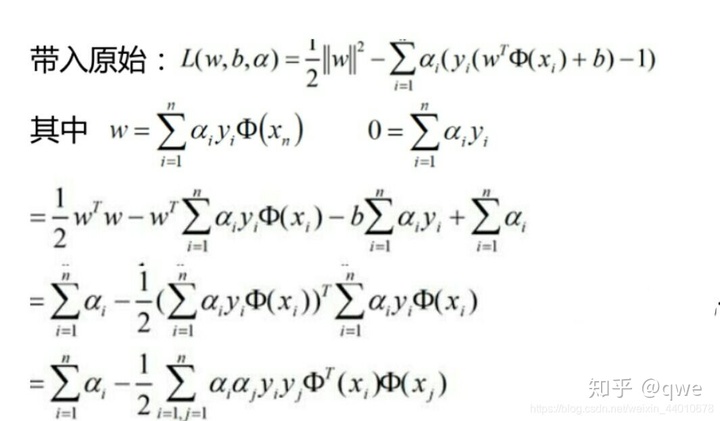
通過上面的推導我們就把求w轉化為了求α,即需要對α求極大值:
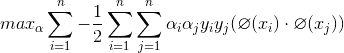
條件:
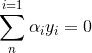
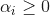
按照常規套路:將求極大值問題轉化為求極小值問題:求一個數的最大值也即求該數相反數的最小值,即:
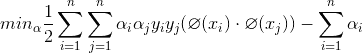
條件不變。
Step 2
α怎么解呢,舉個簡單的例子:
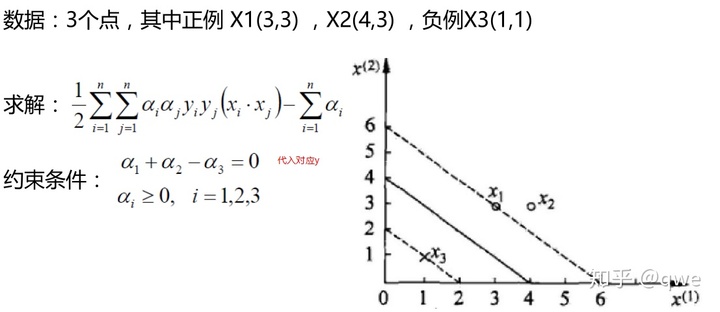
因為x1,x2是正例,所以對應的Y=1,x3是負例,所以對應的Y=-1

分別對α1和α2求偏導,偏導等于0可得α1=1.5,α2=-1。
但是α2<0,和我們的條件αi≥0不相符,所以解應該在邊界點上。
所以分別令α1和α2等于0來計算。
α1=0,α2=-2/13,帶入原式得到-0.153,α2依然小于0,不滿足約束
α1=0.25,α2=0,帶入原式得到-0.25,符合約束。根據α1和α2計算得到α3,α3=α1+α2=0.25。所以最小值在(0.25,0,0.25)處取得。
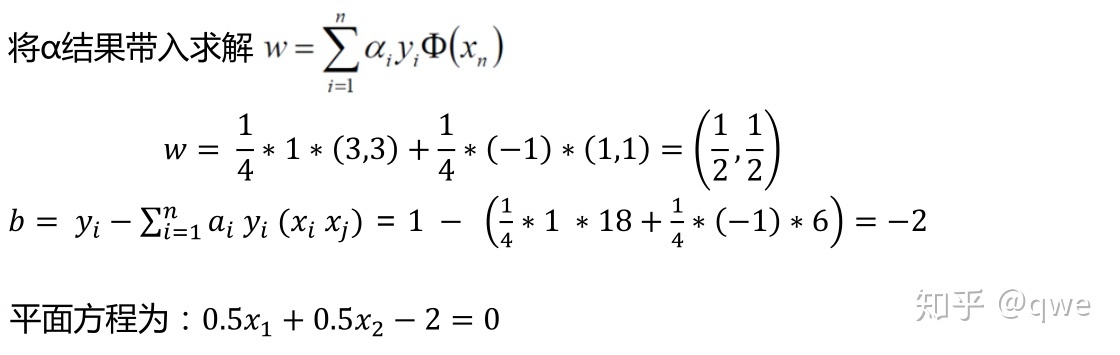
終于解完了……有點想吐的感覺。
————————————————————————————————————
通過上面的這個例子是不是有一點別的發現呢?
通過上面的例子可以知道只有邊界點對應的不為0,即非邊界點對應的均為0,也就是說最終影響w值的只是邊界點(距離決策邊界最近的那些點)這也與我們的求解目標是一致的。此時,我們可以說決策變量是由邊界上的點支持決定的,我們可以叫這些邊界點為支持向量,只有這些支持向量會對結果有影響。據說這也是支持向量機名字的由來。
軟間隔問題
先來觀察一下這個圖:
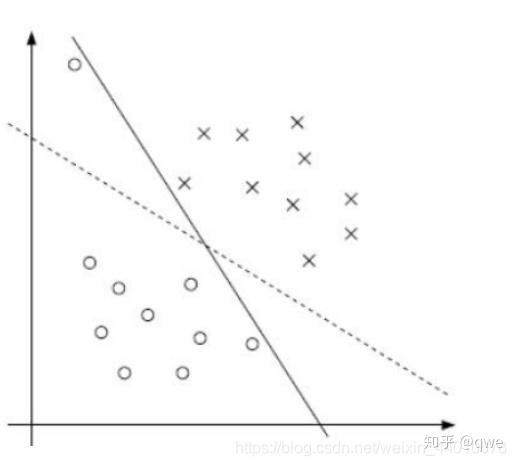
在圖中我們發現一個離群點造成了超平面的移動,間隔縮小了,可以看到模型對噪聲非常敏感。如果這個離群點在另外一個類中時,那我們的模型就線性不可分了。
之前的方法要求把兩類點完全分得開,這個要求有點過于嚴格了,來放松一下!這時候我們給原來的模型加一些條件,即允許這些個別離群點違背限制條件,引入松弛因子:
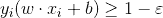
那么新的目標函數為:
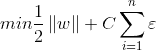
限制條件為:
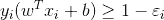
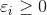
該模型稱為軟間隔,引入的非負參數ξi(松弛變量),引入了這個參數后,可以發現允許一些樣本點的函數間隔小于1,即在最大間隔區間內,或者函數間隔為負,即樣本點在另一個類的區域內。 平白無故的放寬了條件,總是要討回一點債的。因此我們將目標函數進行了調整,用來對離群點進行懲罰,目標函數后面加上的C∑ξi,表示離群點越多,目標函數值越大,而我們要求的是盡可能小的目標函數值,也就是說我在選擇超平面時,要選擇最合適的超平面使離群點的數目最小,這樣目標函數的值就會相對離群點多的時候更小。C是離群點的權重,C越大表明離群點對目標函數影響越大,所以我們不希望超平面分離出更多的離群點。
這里的C是我們需要制定的一個參數。
解法和上面的流程大致相同(這里不多說了):

核變換
接下來主要是談論一下?(x)。看了上面的介紹,是不是有一種這樣的感覺:并沒有覺得SVM厲害在哪里,只是進行了一個線性二分。要是真這樣感覺那就大錯特錯了,不信接著往下看,SVM最厲害的地方出現了。
左邊的圖這些數據分布比較復雜,明顯是線性不可分的。那么有沒有一種方法來分開呢。當然有,那就是把低微不可分問題轉為高維可分的(如右圖)。
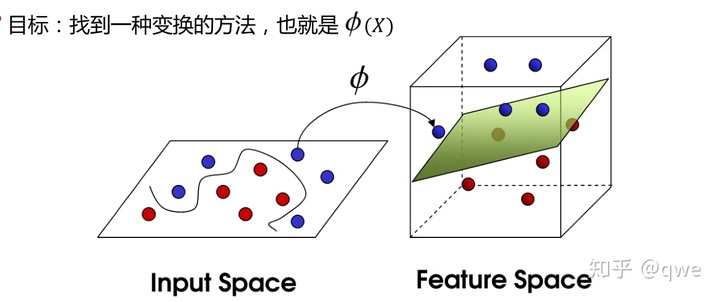
再如下圖:
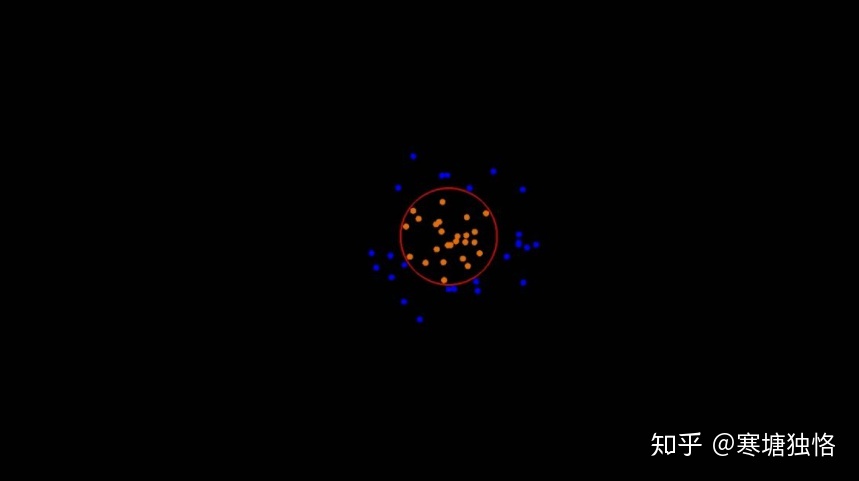
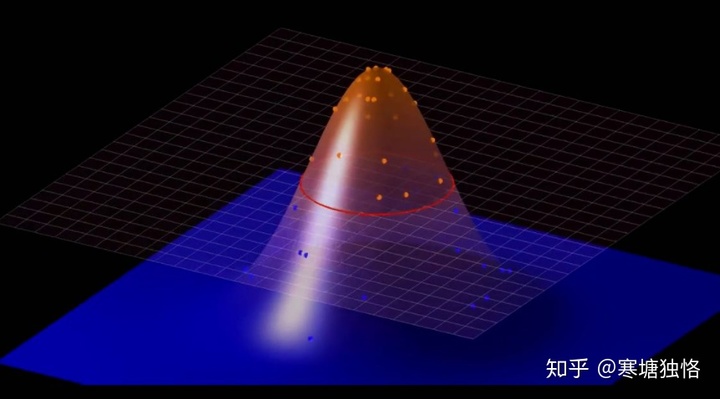
那么接下來給出核函數的定義:
核函數(kernel function)就是指K(x, y) = <f(x), f(y)>,其中x和y是n維的輸入值,f(·) 是從n維到m維的映射(通常,m>>n)。<x, y>是x和y的內積。
再來舉個小小的栗子。
假如現在又兩個數據: x = (x1, x2, x3); y = (y1, y2, y3);
按照SVM和函數理論來說,在3D空間內已經不能進行線性可分了,我們得通過一個函數把它映射到更高維的空間。
令 f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3); f(y)亦然;(實際上就是把特征組合,相當于升維)。由于需要計算內積,所以需要計算在9維下的數據,一想就知道很復雜……
具體到數字:令x=(1,2,3);y=(4,5,6)。那么f(x)=(1,2,3,2,4,6,3,6,9),f(y)=(16,20,24,20,25,36,24,30,36)。此時<f(x),f(y)>=16+40+72…+324=1024。
這些數字比較小,看起來還能應付,但是如果數再大點呢,是不是就很復雜了,甚至沒辦法計算了。
但是發現:K(x, y)=(<x,y>)^2(<x,y>)2
K(x, y)=(4+10+18)^2=1024(4+10+18)2=1024
這種計算方法要比剛才的計算方法簡單很多吧
這也是一個非常重要的特性。在支持向量機中,雖然說是映射到高維空間中去求內積,但是實際中計算的時候并沒有在高維度下計算。只是假設映射到了高維空間,但實際上要的是計算的結果,這個結果在低維空間中計算就可以,然后把這個值映射到高維空間。所以核函數把高維空間的計算轉換為低維空間中計算,實際并沒有映射到高維空間中去。
從低維到高維需要的這個映射就是核函數,那么核函數怎么來指定呢?
常用的核函數是高斯核函數(也稱徑向基 (RBF) 函數,是常用的一種核函數。它可以將有限維數據映射到高維空間)。
在機器中的效果如下:
線性核函數:
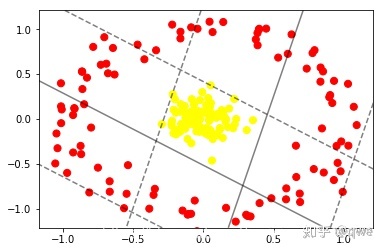
高斯核函數:
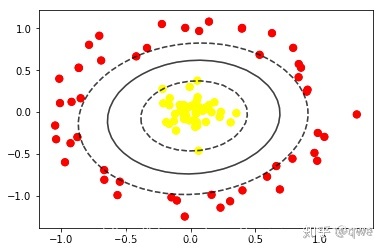


















下啟動MySQL,結果顯示:env: /etc/init.d/mysql:權限不夠。 我已經將權限切換到su了...)
