【轉】利用python的KMeans和PCA包實現聚類算法

?

?

轉自：https://www.cnblogs.com/yjd_hycf_space/p/7094005.html

---

題目： 通過給出的駕駛員行為數據（trip.csv），對駕駛員不同時段的駕駛類型進行聚類,聚成普通駕駛類型，激進類型和超冷靜型3類 。 利用Python的scikit-learn包中的Kmeans算法進行聚類算法的應用練習。并利用scikit-learn包中的PCA算法來對聚類后的數據進行降維，然后畫圖展示出聚類效果。通過調節聚類算法的參數，來觀察聚類效果的變化，練習調參。

數據介紹： 選取某一個駕駛員的經過處理的數據集trip.csv，將該駕駛人的各個時間段的特征進行聚類。（注：其中的driver 和trip_no 不參與聚類）

字段介紹： driver ：駕駛員編號；trip_no：trip編號；v_avg：平均速度；v_var：速度的方差；a_avg：平均加速度；a_var：加速度的方差；r_avg：平均轉速；r_var：轉速的方差； v_a：速度level為a時的時間占比（同理v_b ， v_c ， v_d ）； a_a：加速度level為a時的時間占比（同理a_b, a_c）； r_a：轉速level為a時的時間占比（ r_b, r_c）

聚類算法要求：

（1）統計各個類別的數目

（2）找出聚類中心

（3）將每條數據聚成的類別（該列命名為jllable ）和原始數據集進行合并，形成新的dataframe，命名為new_df ，并輸出到本地，命名為new_df.csv。

降維算法要求：

（1）將用于聚類的數據的特征的維度降至2維，并輸出降維后的數據，形成一個dataframe名字new_pca

（2）畫圖來展示聚類效果（可用如下代碼）：

　import matplotlib.pyplot asplt

? ?d = new_pca[new_df['jllable'] == 0]

? ?plt.plot(d[0], d[1], 'r.')

? ?d = new_pca[new_df['jllable'] == 1]

? ?plt.plot(d[0], d[1], 'go')

? ?d = new_pca[new_df['jllable'] == 2]

? ?plt.plot(d[0], d[1], 'b*')

? ?plt.gcf().savefig('D:/workspace/python/Practice/ddsx/kmeans.png')

? ?plt.show()

?

python實現代碼如下：

from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdf=pd.read_csv('trip.csv', header=0, encoding='utf-8')
df1=df.ix[:,2:]
kmeans = KMeans(n_clusters=3, random_state=10).fit(df1)
df1['jllable']=kmeans.labels_
df_count_type=df1.groupby('jllable').apply(np.size)##各個類別的數目
df_count_type
##聚類中心
kmeans.cluster_centers_
##新的dataframe，命名為new_df ，并輸出到本地，命名為new_df.csv。
new_df=df1[:]
new_df
new_df.to_csv('new_df.csv')##將用于聚類的數據的特征的維度降至2維，并輸出降維后的數據，形成一個dataframe名字new_pca
pca = PCA(n_components=2)
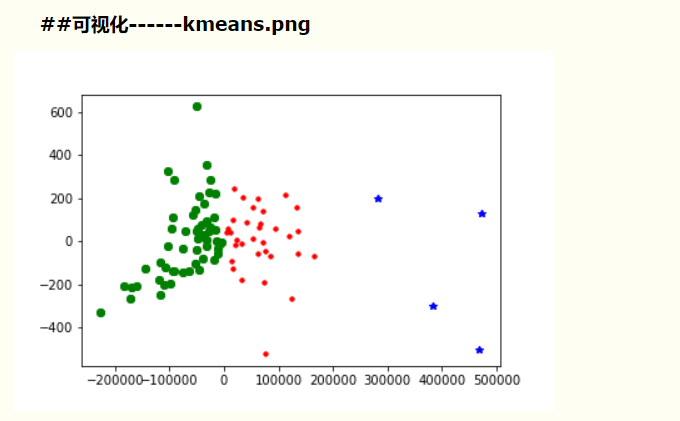
new_pca = pd.DataFrame(pca.fit_transform(new_df))##可視化
d = new_pca[new_df['jllable'] == 0]
plt.plot(d[0], d[1], 'r.')
d = new_pca[new_df['jllable'] == 1]
plt.plot(d[0], d[1], 'go')
d = new_pca[new_df['jllable'] == 2]
plt.plot(d[0], d[1], 'b*')
plt.gcf().savefig('kmeans.png')
plt.show()

　　

?

?