一、堆樹的定義
堆樹的定義如下:
(1)堆樹是一顆完全二叉樹;
(2)堆樹中某個節點的值總是不大于或不小于其孩子節點的值;
(3)堆樹中每個節點的子樹都是堆樹。
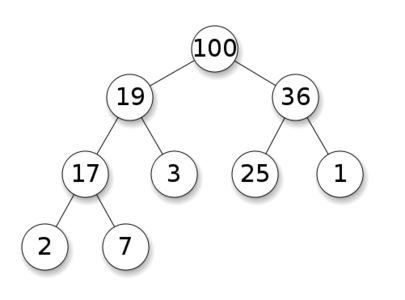
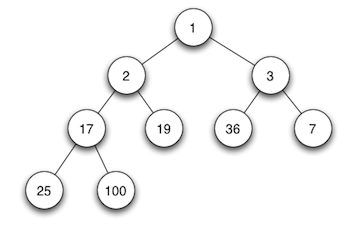
當父節點的鍵值總是大于或等于任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小于或等于任何一個子節點的鍵值時為最小堆。如下圖所示,左邊為最大堆,右邊為最小堆。
二、堆樹的操作
以最大堆為例進行講解,最小堆同理。
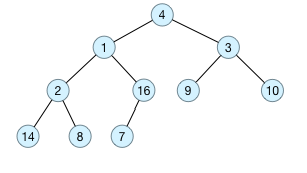
原始數據為a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7},采用順序存儲方式,對應的完全二叉樹如下圖所示:
(1)構造最大堆
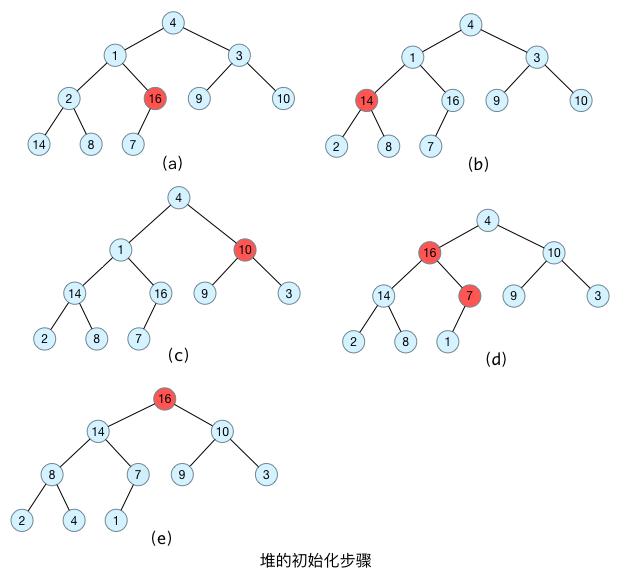
在構造堆的基本思想就是:首先將每個葉子節點視為一個堆,再將每個葉子節點與其父節點一起構造成一個包含更多節點的對。
所以,在構造堆的時候,首先需要找到最后一個節點的父節點,從這個節點開始構造最大堆;直到該節點前面所有分支節點都處理完畢,這樣最大堆就構造完畢了。
假設樹的節點個數為n,以1為下標開始編號,直到n結束。對于節點i,其父節點為i/2;左孩子節點為i*2,右孩子節點為i*2+1。最后一個節點的下標為n,其父節點的下標為n/2。
如下圖所示,最后一個節點為7,其父節點為16,從16這個節點開始構造最大堆;構造完畢之后,轉移到下一個父節點2,直到所有父節點都構造完畢。
C++代碼實現:
定義存放堆的結構如下:
strcut MaxHeap{Etype *heap;int HeapSize;int MaxSize;};MaxHeap H;
其中,heap是數據元素存放的空間,下標從1開始存數數據,下標為0的作為工作空間,存儲臨時數據。HeapSize是數據元素的個數,MaxSize是存放數據元素空間的大小。
初始化堆方法如下:
void MaxHeapInit (MaxHeap &H){for(int i = H.HeapSize/2; i>=1; i--){H.heap[0] = H.heap[i];int son = i*2;while(son <= H.HeapSize){if(son < H.HeapSize && H.heap[son] < H.heap[son+1])son++;if(H.heap[0] >= H.heap[son])break;else{H.heap[son/2] = H.heap[son];son *= 2;}}H.heap[son/2] = H.heap[0];}}
(2)最大堆中插入節點
最大堆的插入節點的思想就是先在堆的最后添加一個節點,然后沿著堆樹上升。跟最大堆的初始化過程大致相同。
C++代碼實現:
void MaxHeapInsert (MaxHeap &H, EType &x){if(H.HeapSize == H.MaxSize)return false;int i = ++H.HeapSize;while(i!=1 && x>H.heap[i/2]){H.heap[i] = H.heap[i/2];i = i/2;}H.heap[i] = x;return true;}
(3)最大堆中堆頂節點的刪除
最大堆堆頂節點刪除思想如下:將堆樹的最后的節點提到根結點,然后刪除最大值,然后再把新的根節點放到合適的位置。
C++代碼實現:
void MaxHeapDelete (MaxHeap &H, EType &x){if(H.HeapSize == 0)return false;x = H.heap[1];H.heap[0] = H.heap[H.HeapSize--];int i = 1, son = i*2;while(son <= H.HeapSize){if(son <= H.HeapSize && H.heap[0] < H.heap[son+1])son++;if(H.heap[0] >= H.heap[son])break;H.heap[i] = H.heap[son];i = son;son = son*2;}H.heap[i] = H.heap[0];return true;}
三、堆樹的應用
利用最大堆、最小堆進行排序。
堆排序算法詳解:http://blog.csdn.net/guoweimelon/article/details/50904231
參考文獻:
1、徹底弄懂最大堆的四種操作(圖解+程序)(JAVA)?http://128kj.iteye.com/blog/1728555
2、最大堆、最小堆?http://blog.csdn.net/genios/article/details/8157031








)
非受管檢測)





)

實現ajax)

