骨牌鋪方格
Time Limit: 2000/1000 MS (Java/Others)????Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 46495????Accepted Submission(s): 22470
Problem Description
在2×n的一個長方形方格中,用一個1× 2的骨牌鋪滿方格,輸入n ,輸出鋪放方案的總數.
例如n=3時,為2× 3方格,骨牌的鋪放方案有三種,如下圖:
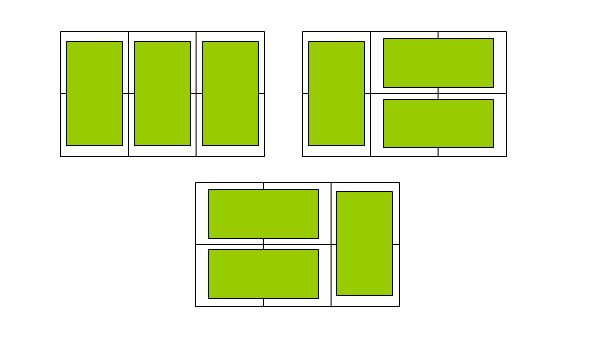
例如n=3時,為2× 3方格,骨牌的鋪放方案有三種,如下圖:

Input
輸入數據由多行組成,每行包含一個整數n,表示該測試實例的長方形方格的規格是2×n (0<n<=50)。
Output
對于每個測試實例,請輸出鋪放方案的總數,每個實例的輸出占一行。
Sample Input
1 3 2
Sample Output
1 3 2
#include<stdio.h>
int sum(int a)
{if(a==1)return 1;if(a==2)return 2;if(a>2){return sum(a-1)+sum(a-2);}
}int main()
{__int64 a;int n;while(~scanf("%d",&n)&&n<=50){a=sum(n);printf("%I64d\n",a);a=0;}return 0;}這個使用循環做法,但是實踐過程中發現運行速度太慢,不建議使用。
#include <stdio.h>
int main()
{int n,j;__int64 a[51];while(scanf("%d",&n)!=EOF){a[1]=1;a[2]=2;for(j=3;j<=n;j++)a[j]=a[j-1]+a[j-2];printf("%I64d\n",a[n]);}
}
然后發現用數組做速度快了好多,省下了好多遞歸調用的時間,所以快很多。
這個題的思路是
1)先鋪好n-1個格,有f(n-1)個方法,再鋪第n層的時候只有一種方法,所以總方法是1*f(n-1);
? ? 2)先鋪好n-2格,有f(n-2)個方法,再鋪后面兩層的時候只能兩個都豎著鋪(否則與第一種情況重復),所以也只有一種情況,總方法數是1*f(n-2)
? ? ? ?推出f(n)=f(n-1)+f(n-2)











)


(轉))

)


