一、概念
全連接層一般在網絡的最后部分做分類輸出,全連接層的有m個輸入和n個輸出,每一個輸出都和所有的輸入相連,相連的權重w都是不一樣的,同時每一個輸出還有一個bias。
二、前向全連接
假設輸入是4,輸出是4,每個輸出點都有一個輸入點的參數,一共4x4=16個w參數,每個輸出點都有一個b參數,一共4個b參數。
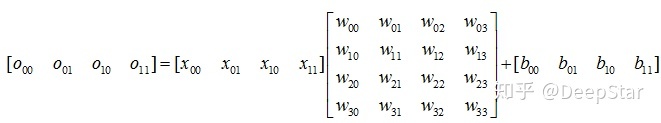
前向全連接的定量分析如下
算力:
BPE byte per element
input feature M*bpe
output feature N*bpe
w參數
b參數 N*bpe
可以看到全連接層的w參數是input feature的N倍,輸入帶寬主要被參數占據。
三、反向全連接gradient傳遞
反向全連接是有兩個2部分,一個是gradient的傳遞,已知
另外是參數gradient求解,已知
假設輸入是4,輸出是4,每個輸出點都有一個輸入點的參數,一共4x4=16個w參數,每個輸出點都有一個b參數,一共4個b參數。
反向全連接gradient傳遞的過程如下:(根據前向公式和求導法則很容易得出)

可以看到weight矩陣進行了轉置
記為
算力為 2MN Flops
三、反向全連接參數gradient求解
參數w gradient求解,已知
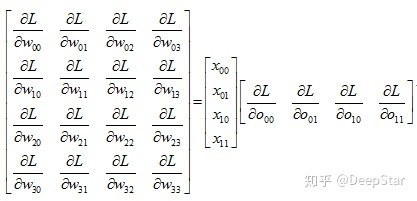
為
算力為 MN mul
參數b gradient求解,已知
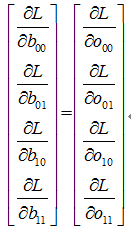
為
兩者就是相等的關系




)


...)











函數(指南))