事先說明:筆者初三,如在敘述中有不嚴謹的地方,還請諸位指出,自當感激不盡。
(本文默認受眾對象為初高中生,因此拋物線一律采取了y=ax2的形式,高中的同學們可以應用旋轉矩陣把它變到y2=2px的形式QAQ筆者懶就不寫咯~)
為了更方便地寫本文,筆者定義一種運算叫實導,就是取冪函數上兩點表示其斜率的運算,下文均記作Fs(ab)或(某代數式)s(a,b指點,方便起見,后文xa,xb,xc對應x1,x2,x3,當運算指對任意兩點求實導時,直接記作Fs)強烈建議初中生閱讀前看看導數!!!
一.新定義的靈感
當時還是在準備三位一體考試,然后為了解極值學習了導數的內容,剛開始百思不得其解,后來從幾何意義出發,了解到導數是一個函數上兩點斜率的極端情況,當兩點無限接近時,所得的切線斜率就是函數該點的導數值。在推理了冪函數形式的導數公式后,恰巧在做錢塘甬真重高的拋物線題目,計算量令人頭大,于是我突發奇想,想要找一種方式簡化運算,剛好想到當兩點不是無限迫近時,兩點斜率是否可以表示,恰好與拋物線陰差陽錯地契合,就發明了這個運算,取可見兩點斜率之意,改導數為實導了。(事實上,根據點差法,可以給出所有冪函數(次數為整數)類型的實導運算及其運算公式,下文將會提到。)
實導運算性質(推導你們自己弄吧hiahiahia奸笑jpg)
1.對于冪函數f(x)=x^n,Fs=x1^n-1 +x1^n-2·x2+x1^n-3·x22……+x2^n-1,(n∈正整數)
若F(x)=x^-n,Fs=-(x^n)s/(x1x2)^n,(n∈正整數)
規定當n=0時,Fs=0
2.若F(x)=h(x)+g(x),則(F(x))s=(h(x))s+(g(x))s
3.若F(x)=h(x)·g(x),則(F(x))s=(h(x))s·(g(x1)+g(x2))/2+(g(x))s·(h(x1)+h(x2))/2
4.后文將Fs2+1記為M
5.鏈式求導法則,隱函數求導法則對于求實導依然有效
二.正文部分一:實導對于拋物線
設f(x)=ax2+bx+c,根據上面運算可知Fs=a(x1+x2)+b(由此可知,當xa+xb=xc+xd時,ab∥cd)
特殊時:1.x1=0,Fs=ax2+b
2.a點為頂點M,則Fs(aM)=a△x(△x=x1-xM)(一般化:Fs=a(△x1+△x2))
3.很容易得知Fs(ab)=F(a+b/2)’(有興趣的可以去查一下數學史中阿基米德求弓形面積,這可能是最早的微分思想了)
4.設割線l:y=【a(x1+x2)+b】x+z,將(x1,ax12+bx1+c)代入,可以解得直線方程:y=Fsx+c-ax1x2,即為拋物線割線公式。
5.同理可以給出拋物線切線公式:y=f(x)’x+c-ax02=(2ax0+b)x+c-ax02
6.任意兩點距離公式:√M·|x1-x2|
三.征途開始:利用上述公式推出更美麗的公式。
α:拋物線內接三角形(△abc)面積公式:S=|a(x1-x2)(x1-x3)(x2-x3)|/2
證明:我們先畫一個三角形:
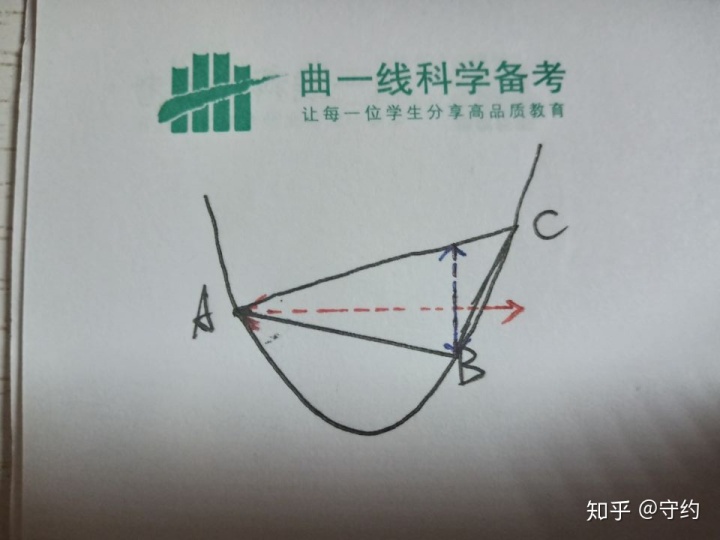
采取中學慣用的方法:水平寬乘鉛垂高,做出h和l,很明顯:
l=(x3-x1)
h=(Fs(AC)-Fs(AB))·(x2-x1)=【a(x1+x3)+b-a(x1+x2)-b】·(x2-x1)
=a(x3-x2)·(x2-x1)
∴S=1/2l·h=|a(x1-x2)(x1-x3)(x2-x3)|(這里我們不知道ABC具體位置,所以加上了絕對值)
是不是充滿了對稱的美學!!!簡單而漂亮!!!
說到這不得不提到一類初中極多的水平寬乘鉛垂高問題,大致就是確定了A和B的位置,然后在其間有動點C,求S△ABCmax,利用上式,我們可以輕松得到當x3=x1+x2/2時,Smax=1/8|a(x1-x2)3|,一直堅信代數據死算的同學們有沒有覺得感情被欺騙了(實際上從幾何意義上考慮,當x3=x1+x2/2時,C點切線恰好與AB平行,此時顯然三角形高最大)
同樣的,對于反比例函數同樣有一般美麗的公式,我就提一下:S=|k(x1-x2)(x1-x3)(x2-x3)/2x1x2x3|
當這類模型轉向四邊形時,同樣會成立。
β:斜率專題:過定點和旋轉。
p1:旋轉的割線(初中常有)
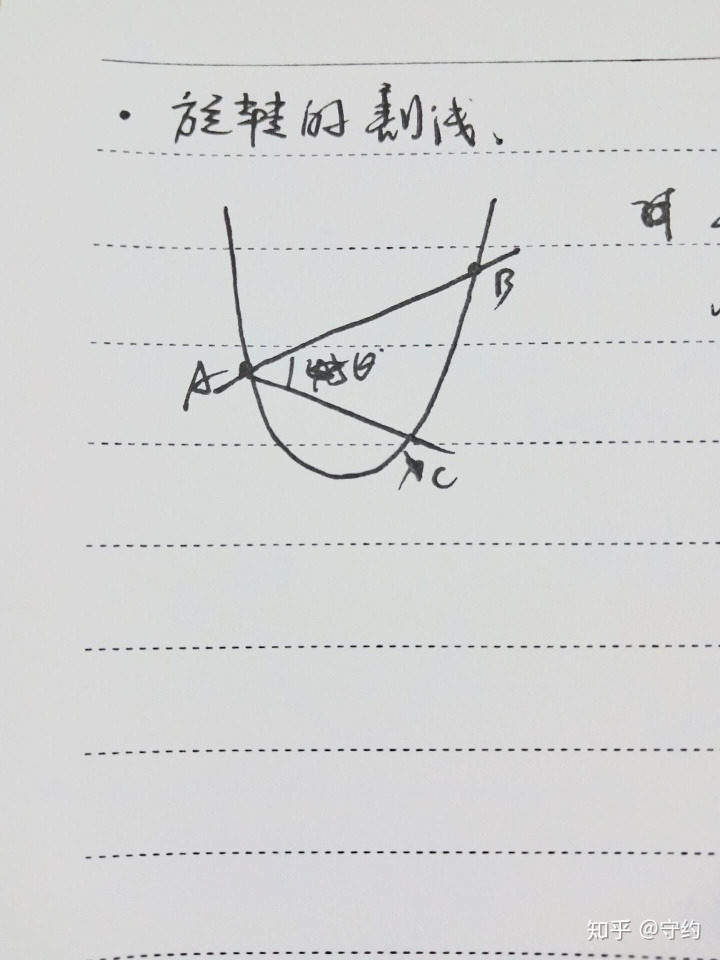
順時針:△Fs=(Fs(AB)-tanθ)/(1+Fs(AB)tanθ)-Fs(AB)
=-tanθ(Fs(AB)2+1)/(1+Fs(AB)tanθ)
=M/(-Fs(AB)-cotθ)
逆時針:同理可得△Fs=M/(-Fs(AB)+cotθ)
總結一下,△x=M/a(-Fs(AB)±cotθ),順時針取負號,逆時針取正號(和三角函數一樣)
p2:斜率之積決定過定點問題。
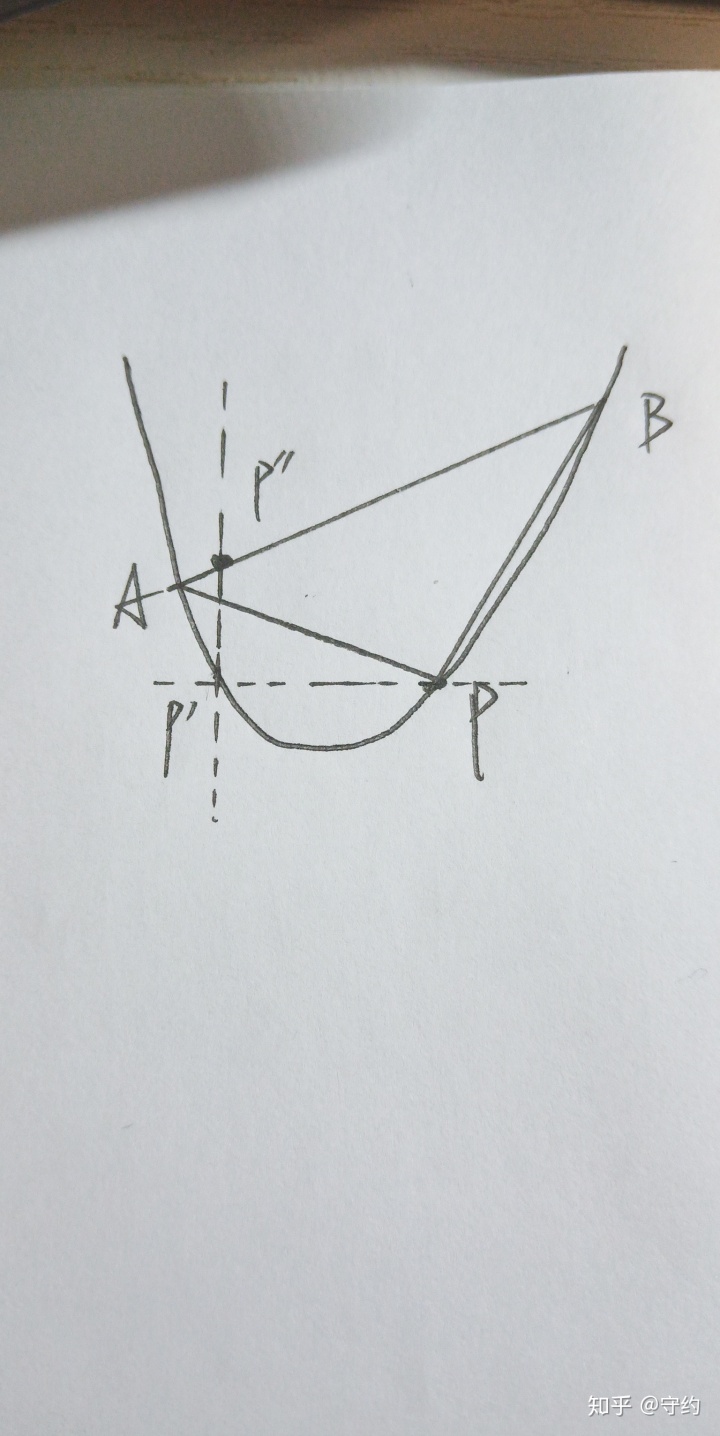
證明:Fs(AP)·Fs(BP)=a2(x1+x0)(x2+x0)=λ①,lAB:y=a(x1+x2)x-ax1x2=kx+b②
①展開并整理,有a2【x02+(x1+x2)x0+x1x2】=a2(x02+kx0/a-b/a)=a2x02+akx0-ab=λ,于是有k=b/x0+λ/ax0-ax0,代入②得y=(b/x0+λ/ax0-ax0)x+b=(x/x0+1)b+λx/ax0-ax0x,很明顯,當x=-x0時,就會有y=ax02-λ/a(定值),在圖形上看,就是取P點關于對稱軸的對稱點,并將縱坐標-λ/a,即得定點P”
要注意的是,該結論逆定理仍然成立,并且其特殊情況(λ=-1)經常會在三一考試中出現,該結論是該類型題目的推廣(吧)
p3:如圖:
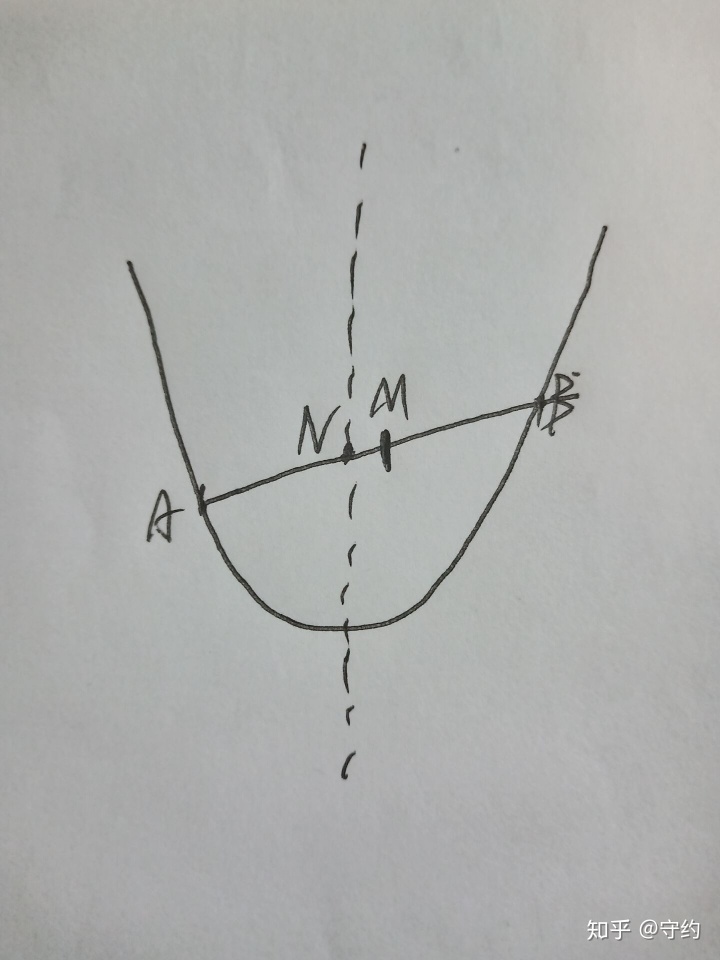
不妨將曲線標準化,取y=ax2,N(0,n)其它情況都可通過平移得到(下文模型默認標準化)
則有lAB:y=a(x1+x2)x-ax1x2=kx+n,故M(x1+x2/2,a(x12+x22)/2)
則xm=k/2a,ym=a/2 ·【(x1+x2)2-2x1x2】=n+k2/2a
即M(k/2a,n+k2/2a)
γ:七仙女模型(瞎取的名字)
在介紹這些模型之前,首先介紹一個結論:
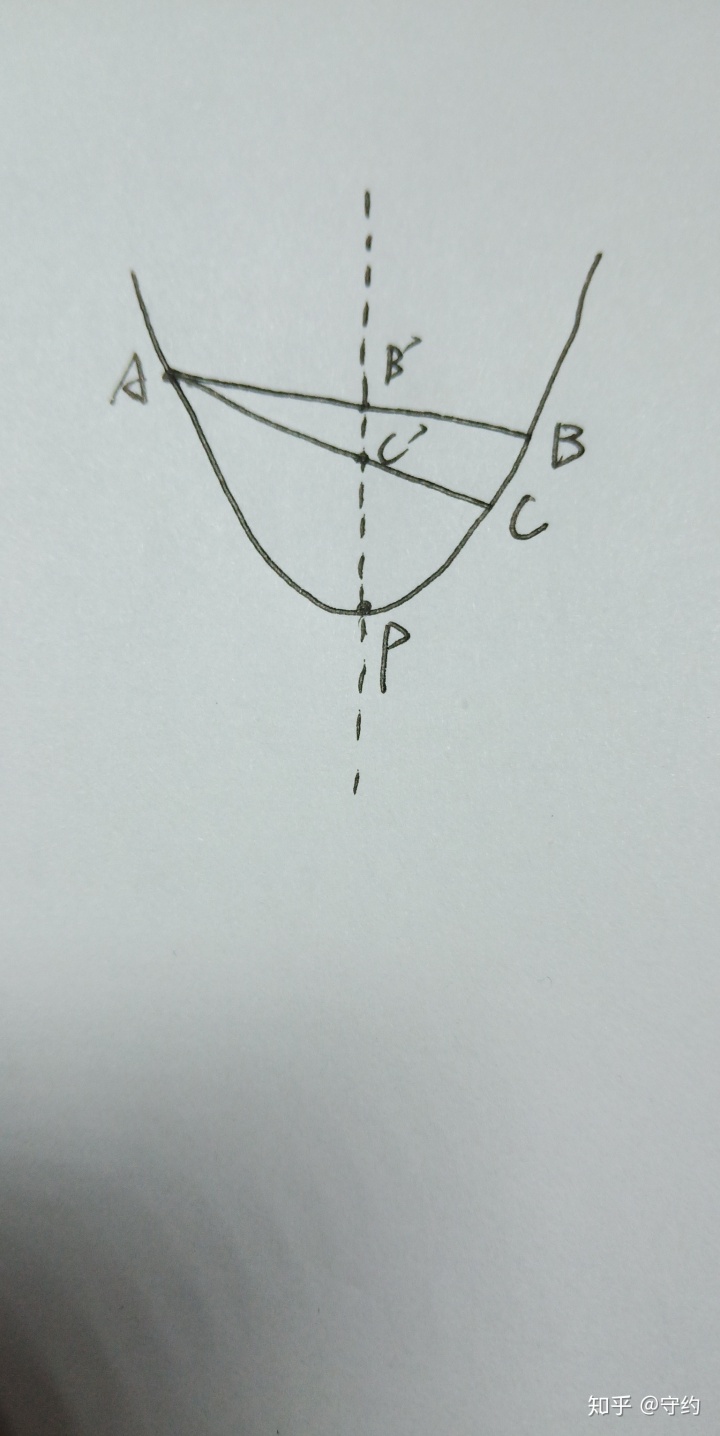
證明:標準化后,yc’=-ax1x3,yb’=-ax1x2,于是向量PC'=yc',向量PB'=yb',兩者相比即向量PC’/向量PB’=x3/x2,再轉化到一般情況,則變成向量PC’/向量PB’=△x2/△x1
我稱之為半割模型。
a.
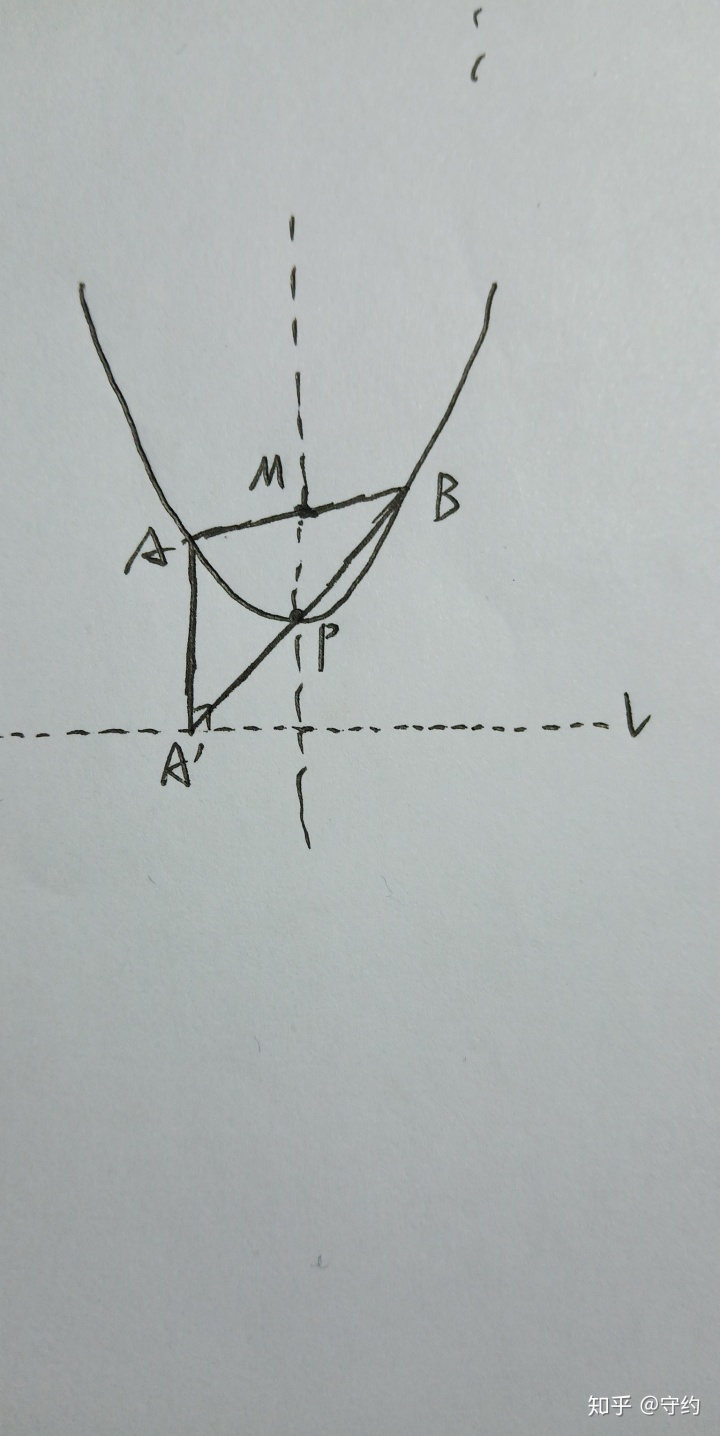
簡述:在拋物線對稱軸上取一點M(0,m),并取直線l:y=-m(接下來6個模型都是如此)
過M的動弦AB交拋物線于A、B,過A(B)作垂線AA'(BB')⊥l,則有A'PB(B'PA)三點共線。
證明:過B作直線l’∥l,交拋物線于C,由半割,知
y2/m=-x2/x1,變形后,有y2/x2=m/-x1,即kA'P=kBP,于是A'PB(B'PA)三點共線。證明相當簡潔。
b.
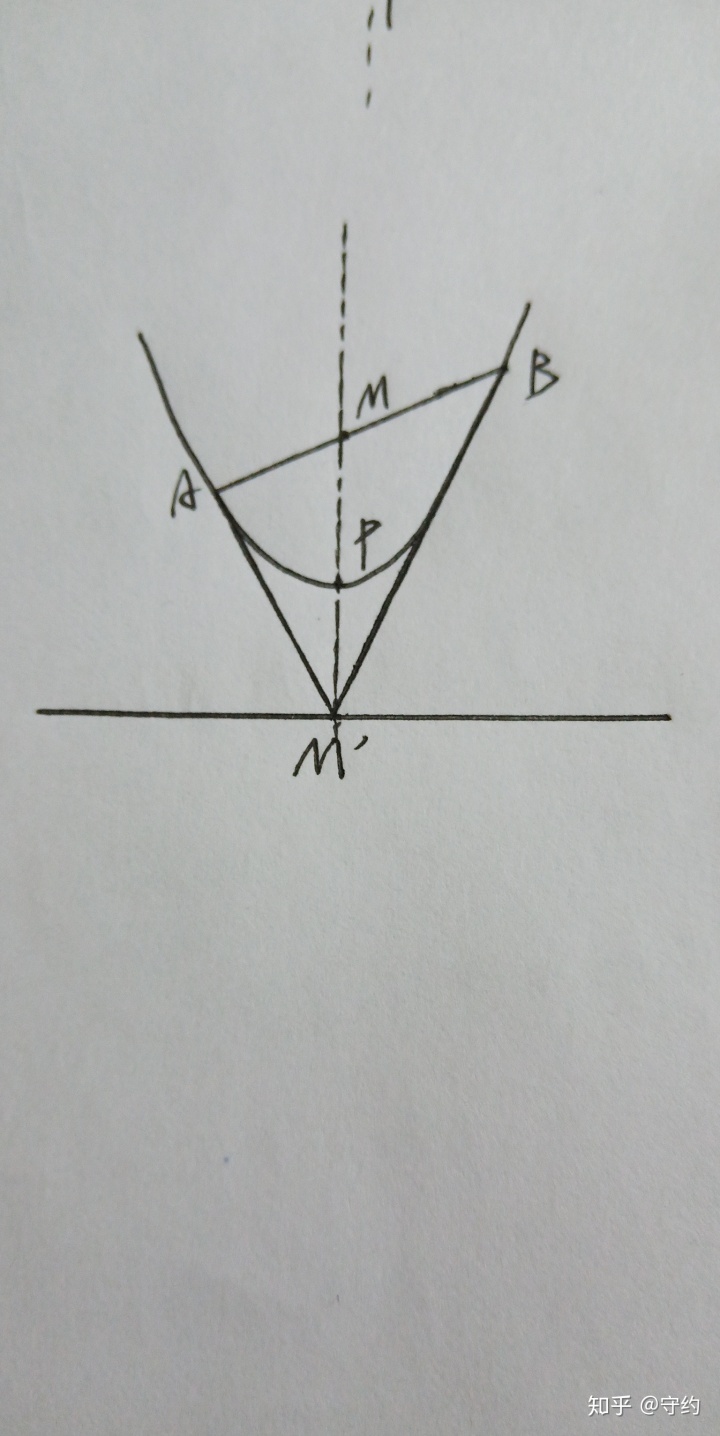
證明:過B作直線l’∥l,交拋物線于C,由半割,知
y2/m=-x2/x1。又kBM’=y2+m/x2,kAM'=y1+m/x1,且-ax1x2=m,
∴x1=-x2m/y2,y1y2=m2,即y1=m2/y2,代入前式化簡后即可得到kBM'=-kAM',得證
c.
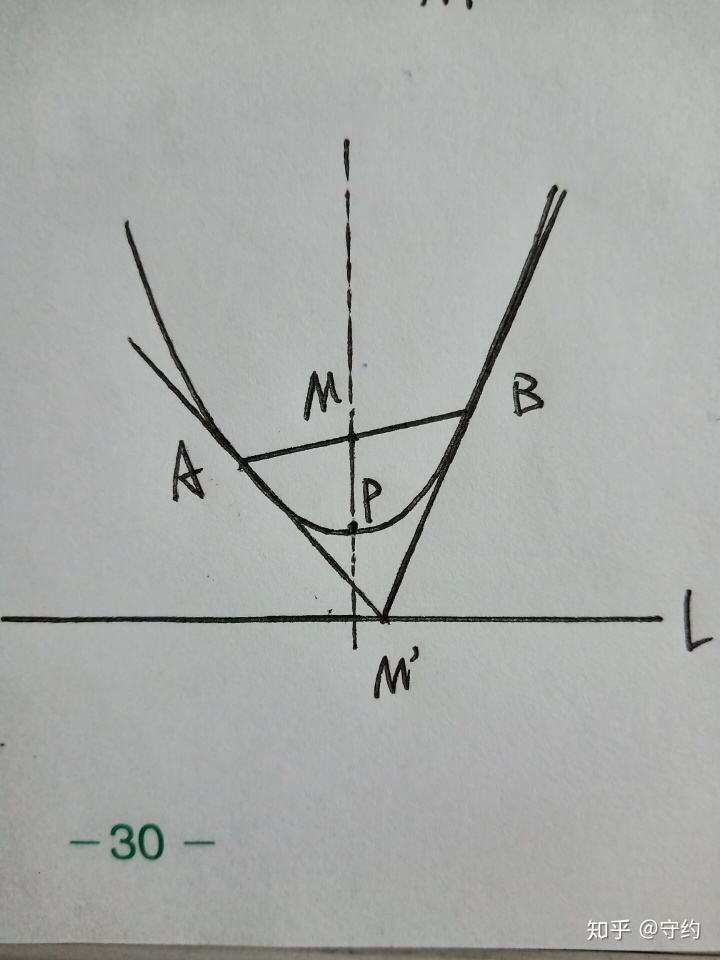
證明:直接聯立切線方程:
la:y=2ax1x-ax12,lb:y=2ax2x-ax22,聯立后得到點M’(x1+x2/2,ax1x2),又因為ym=-ax1x2,所以得證。
對此不得不加以補充:若過M’作直線l’平行于y軸,交拋物線于C,交AB于D,經過計算可以發現C是M’D的中點,而且S△ABC恰好=1/8|a(x1-x2)3|,于是我們就得到S△ABM=1/4|a(x1-x2)3|,十分神奇
d.
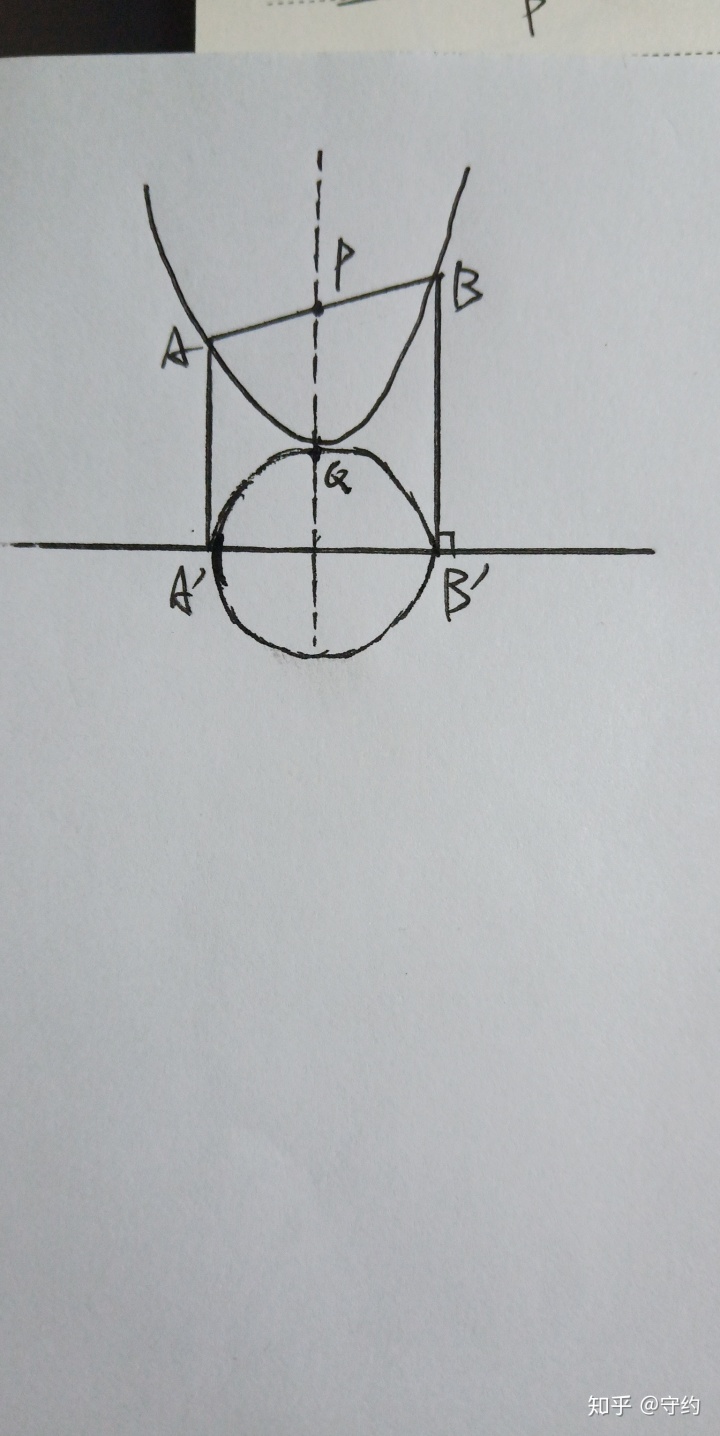
設P(0,m)=(0,-ax1x2)不妨就設圓與拋物線對稱軸交于Q,則∠A'QB'=90°,令對稱軸與l交于P',則由射影定理,有QP'2=A'P'·P'B',∴(yQ+m)2=-x1x2=m/a
最終可解得yQ=√m/a -m,特殊地,當P為焦點時,Q與P重合。
e,f.
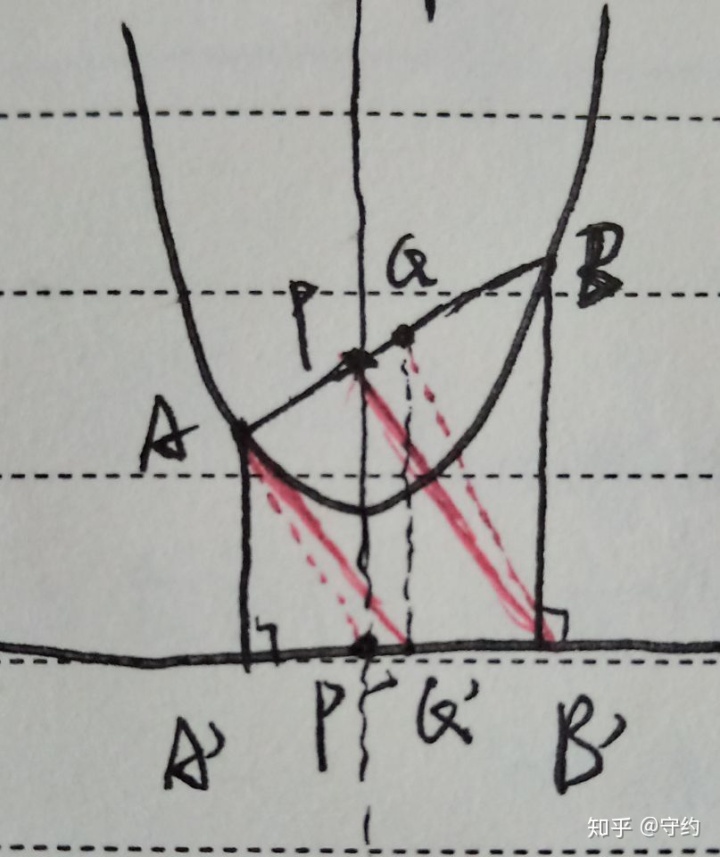
證明:直接設點(我省略了)
kAP'=2ax1x2/x1=2ax2,kQB'=(ax1x2-ax22)/(x1-x2)/2=2ax2(x1-x2)/x1-x2=2ax2
kAQ'=-a(x1-x2)2/2/x1-x2/2=-a(x1-x2),kP'B=ax2(x1-x2)/-x2=-a(x1-x2)
∴kAP’=kQB',kAQ'=kP'B,即得證。
g.
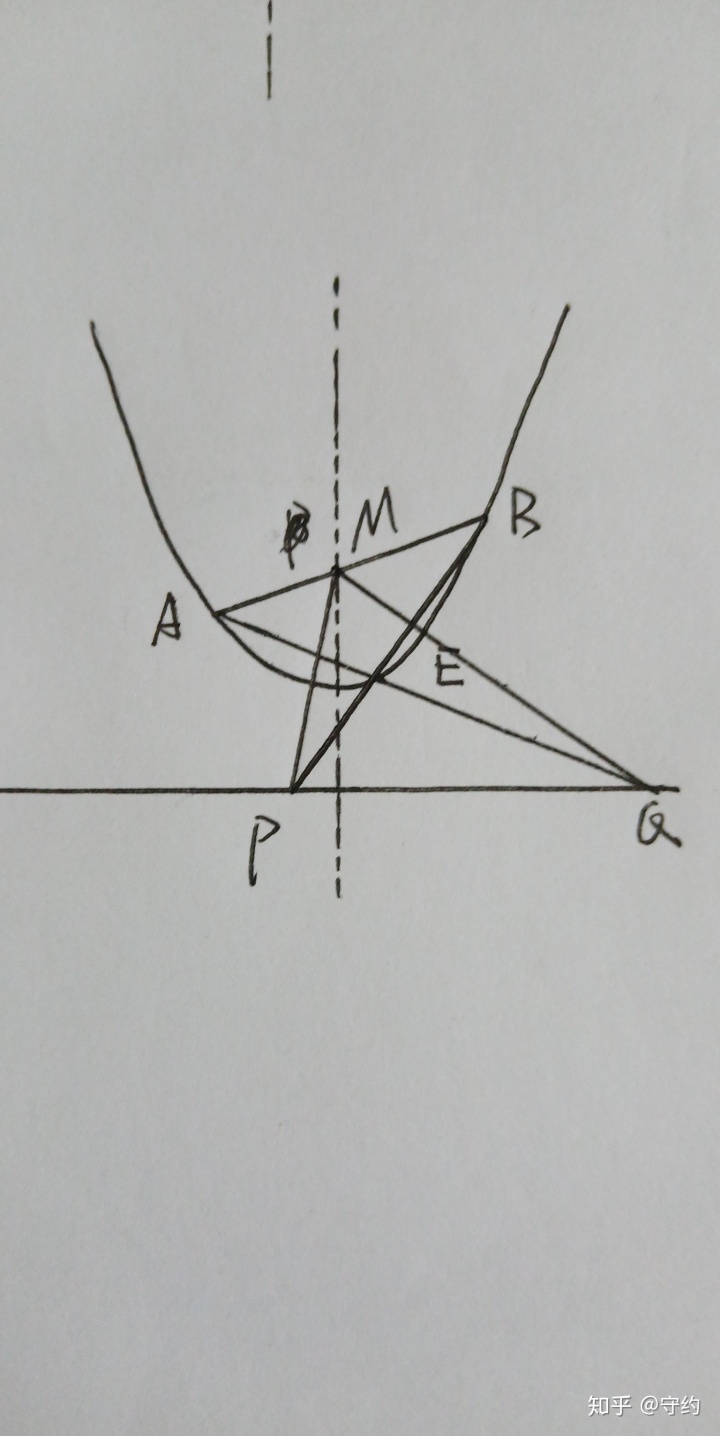
證明:A(x1,ax12)B(x2,ax22)E(x0,ax02)
于是lBE:y=a(x0+x2)x-ax0x2,lAE:y=a(x0+x1)-ax0x1
代入y=-m,分別解得P(x2(x0+x1)/(x0+x2),-m),Q(x1(x0+x2)/(x0+x1),-m)
∴kPM=-2m(x0+x2)/x2(x0+x1),kQM=-2m(x0+x1)/x1(x0+x2)
∴kPM·kQM=4m2/x1x2=4m2/-a/m=-4am
特殊地,當M為焦點,PM⊥MQ
四.小試牛刀(例題解析)
1.來自錢塘甬真重高某卷
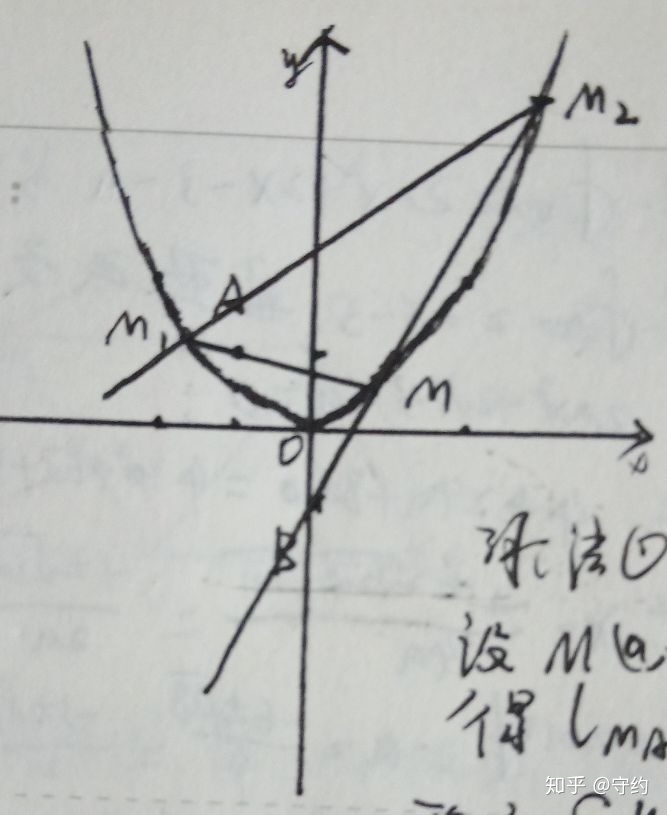
解:不妨將未知點看成已知定點,那么M,M1,M2就是與之關聯的動點。
設lMM1:y=k(x+1)+1=?(xm+xm1)x-?xmxm1=?(xm+xm1)(x+1)+1,于是 -?xmxm1=?xm+?xm1+1,化簡得xmxm1=-(xm+xm1+2)①
kBM=?xm2+1/xm=?xm+1/xm=Fs(MM2)=?xm+?xm2,∴xm2=2/xm②
所以ym1m2=?(xm1+xm2)x-?xm1xm2,將②代入有:
ym1m2=?(xm1xm+2)/xm·x-xm1/xm,將①代入有:-?x-(xm1+?xm1·x)/xm
∴當x=-2時,y=1,即過定點Q(-2,1)
標答的話就是硬算,我沒什么好說的,我按照標答做的時候算錯了兩遍。。。
2.2018浙江嵊州高三期末質檢21
已知拋物線y=x2,A(-1,1),B(4,-2)拋物線上一點P(x,y)(x<-1),AP與y軸交于Q,記△PAB,△QAB面積分別為S1,S2。
(1)若AP⊥PB,求x
(2)求(S1-5S2)min
(1)解:由題知Fs(AP)·Fs(BP)=(x-1)·(x+2)=x2+x-2=-1
解得x=-1+√5/2(舍)x=-1-√5/2
(2)解:S1=(-1-x)(2-x)(2+1)/2=3(x2-x-2)/2
yQ=-(-1·x)=x,∴S2=h·l/2=3(2-x)/2
∴(S1-5S2)=3(x2-x-2)/2-15(2-x)/2=3x2+12x-36/2=3(x+2)2-48/2
則當x=-2時,原式min=-24
(3)2019浙江臺州一中、天臺一中高三上期中21
已知直線PA,PB與拋物線y=?x2分別相切于A,B
(1)若P在直線y=-1上,求證:直線AB過定點
(2)若點P是半橢圓?x2+?y2=1(y<0)上的動點,求S△PAB的取值范圍
(1)證明:由上結論易知AB過定點(0,1)
(2)令xa=x1>xb=x2,∴S△PAB=(x1-x2)3/16,且x1+x2=2xp,?x1x2=yp
∴(x1+x2)2-4x1x2=4xp2-16yp=(x1-x2)2
∴S△PAB=√xp2-4yp 3/2,又∵3x2+4y2=12,∴xp2=4 -4yp2/3,代入得:
S△PAB=√-4yp2/3-4yp+43/2,∴當y=-3/2時,S△PABmax=7√7/2
當y=0時,S△PAB=4,又因為取不到0,所以4<S△PAB≤7√7/2
類似的例題還有很多,我不列舉了
求贊~






的創建、掛載與刪除...)












