簡單選擇排序的原理
簡單選擇排序的原理非常簡單,即在待排序的數列中尋找最大(或者最小)的一個數,與第 1 個元素進行交換,接著在剩余的待排序的數列中繼續找最大(最小)的一個數,與第 2 個元素交換。以此類推,一直到待排序的數列中只有一個元素時為止。
也就是說,簡單選擇排序可分為兩部分,一部分是選擇待排序的數列中最小的一個數,另一部分是讓這個數與待排序的數列部分的第1個數進行交換,直到待排序的數列只有一個元素,至此整個數列有序。
這個算法非常簡單,其排序過程如
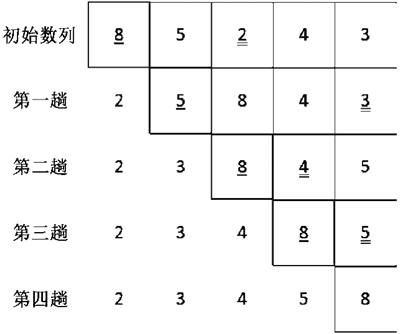
圖 1 簡單選擇排序的排序過程
其中的方框部分為待排序的數列部分,雙下畫線的元素為待排序的數列中最小的元素,單下畫線的元素為待排序的數列的首元素,每一趟讓它們進行交換,最終得到有序數列。
簡單選擇排序的實現
簡單選擇排序的實現代碼如下:
public class SelectSort {
private int[] array;
public SelectSort(int[] array) {
this.array = array;
}
public void sort() {
int length = array.length;
for (int i = 0; i < length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}
}
public void print() {
for (int i = 0; i < array.length; i++) {
System.out.println(array[i]);
}
}
}
通過代碼,我們發現這個算法其實挺爛的,而且應該有可以優化的方法,這里先賣個關子。測試代碼如下:
public class SortTest {
public static void main(String[] args) {
testSelectSort();
}
/**
* 簡單選擇排序
*/
private static void testSelectSort() {
int[] array = {5, 9, 1, 9, 5, 3, 7, 6, 1};
SelectSort selectSort = new SelectSort(array);
selectSort.sort();
selectSort.print();
}
}
選擇排序的特點及性能
由于在簡單選擇排序中,我們一般在原本的待排序的O(1)。
在最好的情況下,每次要找的最大(或者最小)的元素就是待排序的數列的第1個元素,也就是說數列本身有序,這樣我們只需要一次遍歷且不需要交換,即可實現一趟排序;而在最壞的情況下,每次在數列中要找的元素都不是第 1 個元素,每次需要交換。比較的次數只與數列的長度有關,而在外部要遍歷整個數列,也與長度有關,所以這樣的雙重循環不管在什么情況下,O(n2)。
但由于選擇排序不需要一個一個地向前移動,而是直接交換,而比較所消耗的 CPU 要比交換所消耗的 CPU 小一些,所以選擇排序的時間復雜度相對于
簡單選擇排序的優化
通過選擇排序的思想,我們知道選擇排序的一個重要步驟是在待排序的數列中尋找最大(或者最小)的一個元素,那么如何尋找這個元素就成為一個可以優化的點。
另外,我們每次都要尋找兩個值中一個是最大值,一個是最小值。這時如果需要將數列從小到大排列,就要把最小值與待排序的數列的第1個元素進行交換,把最大值與待排序的數列的最后一個元素進行交換。這樣我們一次就能尋找兩個元素,使外層循環的時間縮短了一半,性能也提高了很多。而且通過一次遍歷就可以直接找出兩個最值,并沒有其他性能損耗。這種一次找兩個值的選擇排序的算法實現,留給讀者自己去嘗試。
選擇排序的適用場景
簡單選擇排序并不很常用,它只是選擇排序的一個思想基礎,選擇排序還有其他方案可以實現。在理解了簡單選擇排序之后,我們就更容易理解和學習其他方案了。選擇排序的用途非常廣泛,之后我們繼續講解如何使用它們。

)

)
...)
)













