歡迎關注公z號：沈陽奧數

兩條直線相交所成的四個角中，有一個角是直角時，就說這兩條直線互相垂直，其中一條直線叫做另一條直線的垂線，它們的交點叫垂足。

如圖，直線AB與CD垂直于點E，記作：AB⊥CD于點E。

通過∠BEC=90°可以判定AB⊥CD；反過來可以通過垂直判斷直角，即如果AB⊥CD那么∠BEC=90°。

垂線的性質：

(1)在同一平面內，過一點有且只有一條直線與已知直線垂直。

(2)連接直線外一點與直線上各點的所有線段中，垂線段最短。簡單說成：垂線段最短。

點到直線的距離：

直線外一點到這條直線的垂線段的長度，叫做點到直線的距離。

下面用一些例子來理解一下這些性質

例題1：如圖，已知AB⊥BC，EA是∠BAD的角平分線，ED是∠ADC的角平分線，AE⊥DE，求證DC⊥BC。

想證明DC⊥BC，根據垂直的定義，如果∠C是直角那么就可以得到結論。

因為AE⊥DE，所以∠AED=90°(根據垂直，可以得出∠AED是直角。相比直接給出角的度數，垂直就是一個隱藏的已知條件，即隱藏著∠AED=90°)，根據三角形內角和，∠EAD+∠EDA=90°。

因為EA，ED是∠BAD，∠ADC的角平分線，所以∠BAE=∠EAD，∠EDC=∠EDA

所以∠BAD+∠CDA=2(∠EAD+∠EDA)=180°，所以AB//CD(同旁內角互補，兩直線平行)。因為AB⊥BC，所以∠B=90°，∠C=180°-∠B=90°(兩直線平行，同旁內角互補)，所以DC⊥BC。

垂線段最短(點到直線的距離)

如圖，直線AB外的點P，過點P做PC⊥AB于點C，那么PC就是垂線段。

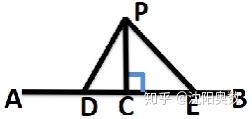
如果D，E是直線AB上任意另外兩點，根據垂線段最短可知PC＜PD，PC＜PE。

我們再從直角三角形的角度驗證一下：因為PC⊥AB，所以∠PCE是直角，在直角三角形PCE中，PC是直角邊，PE是斜邊。由于直角三角形中直角邊小于斜邊，所以PC＜PE。或者根據勾股定理PC2+CE2=PE2，由于CE2﹥0，所以PC2＜PE2，即PC＜PE。這些道理都是相通的，可以相互驗證。

這個垂線段的長度，叫做點P到直線AB的距離。它是非常重要的，在今后坐標系中的幾何題中，會經常出現。由垂線段的這個性質，可以延伸到平行線間的距離。