接觸全排列已經好長時間了,一直沒有抽空總結一下全排列的相關問題,下面來說一下!
排列
一般地,從n個不同元素中取出m(m≤n)個元素,按照一定的順序排成一列,叫做從n個元素中取出m個元素的一個排列(Arrangement)。特別地,當m=n時,這個排列被稱作全排列(Permutation)。
排列數公式:

下一個全排列算法
lintcode鏈接:http://www.lintcode.com/zh-cn/problem/next-permutation/
樣例
左邊是原始排列,右邊是對應的下一個排列。
1,2,3?→?1,3,2
3,2,1?→?1,2,3
1,1,5?→?1,5,1
下一個全排列算法——first
class Solution { public:/*** @param nums: a vector of integers* @return: return nothing (void), do not return anything, modify nums in-place instead*/void nextPermutation(vector<int> &nums) {//調用<algorithm>中的下一個排列算法以及排序算法if(!next_permutation(nums.begin(), nums.end()))sort(nums.begin(), nums.end(), less<int>());
}
}
下一個全排列算法——second
class Solution { public:/*** @param nums: a vector of integers* @return: return nothing (void), do not return anything, modify nums in-place instead*/void nextPermutation(vector<int> &nums) {int ld = -1;if(nums.size() < 1) return ;for(int i=nums.size()-2; i>=0; --i)//找到從右邊開始第一個比它右邊相鄰小的數的位置if(nums[i] < nums[i+1]){ld = i;break;}if(ld != -1){//找到從右邊開始,第一個比位置為ld所在數 大的數的位置int rd;for(int i=nums.size()-1; i>=0; --i)if(nums[ld] < nums[i]){rd = i;break;}swap(nums[ld], nums[rd]);//在交換之前,ld位置后面的已經是從大到小排好序的,已經沒有下一個排列了sort(nums.begin()+ld+1, nums.end());//交換之后,將ld后面的數置為最小的排列,從小到大排序 }if(ld == -1){sort(nums.begin(), nums.end());}} };
下一個全排列算法——third
class Solution { public:/*** @param nums: a vector of integers* @return: return nothing (void), do not return anything, modify nums in-place instead*/void nextPermutation(vector<int> &nums) { //挑戰不使用額外的空間, 其實和方法二的思路是一樣的int n = nums.size();for(int i=n-1; i>=0; --i)for(int j=n-1; j>i; --j)if(nums[i] < nums[j]){swap(nums[i], nums[j]);sort(nums.begin()+i+1, nums.end());return ;}sort(nums.begin(), nums.end());} };
下一個全排列的思想:
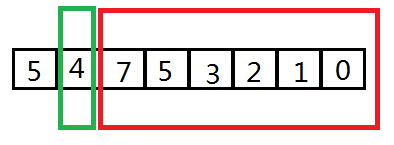
?
如上圖所示,該全排列對應的下一個全排列是和綠色框里的數字以及紅色框里的數字有關系的。顯而易見的是紅色框里的數列已經沒有下一個排列了,因為已經是一個遞減的序列了。為了得到下一個排列,我們將綠色框里的數字和紅色框里右邊起第一個比綠色框中數字大的數字交換位置(也就是4 和 5交換位置)。這樣還不是下一個全排列,交換之后紅色框內的序列為7 4 3 2 1 0, 將它變成遞增序列 0 1 2 3 4 7,就得到了下一個全排列。
因為,一個全排列,末尾的一段區間肯定是遞減的(如上圖的紅色框區間),如果這段區間一直延伸到首部,那么也就沒有下一個全排列了,否則找到和這段區間最近的一個數字(上圖中綠色框中的數字),然后經過上述的處理就可以得到下一個全排列了。
the second method 就是先找到綠色框數字的位置(ld), 然后在尋找紅色框中右邊第一個比綠色框中數字大的數字的位置(rd);
the third method的意思就是從右邊開始尋找第一對(i, j),滿足nums[i]<nums[j], 對應second method中(ld, rd)。該方法沒有用到額外的存儲空間。
上一個全排列算法
注:算法思想和下一個全排列的思想正好相反,步驟一致!
? ?lintcode鏈接:http://www.lintcode.com/zh-cn/problem/previous-permutation/
樣例
給出排列[1,3,2,3],其上一個排列是[1,2,3,3]
給出排列[1,2,3,4],其上一個排列是[4,3,2,1]
上一個全排列算法——first
class Solution { public:/*** @param nums: An array of integers* @return: An array of integers that's previous permuation*/vector<int> previousPermuation(vector<int> &nums) { //直接調用<algrotihm>中的算法prev_permutation()if(!prev_permutation(nums.begin(), nums.end()))sort(nums.begin(), nums.end(), greater<int>());return nums; } };
上一個全排列算法——second
class Solution { public:/*** @param nums: An array of integers* @return: An array of integers that's previous permuation*/vector<int> previousPermuation(vector<int> &nums) { int ld = -1;if(nums.size() <= 1) return nums;for(int i=nums.size()-2; i>=0; --i)//找到從右邊開始第一個比它右邊相鄰大的數的位置if(nums[i] > nums[i+1]){ld = i;break;}if(ld != -1){//找到從右邊開始,第一個比位置為ld所在數 小的數的位置int rd;for(int i=nums.size()-1; i>=0; --i)if(nums[ld] > nums[i]){rd = i;break;}swap(nums[ld], nums[rd]);//在交換之前,ld位置后面的已經是從小到大排好序的,已經沒有上一個排列了//交換之后,將ld后面的數置為最大的排列,從大到小排序sort(nums.begin()+ld+1, nums.end(), greater<int>());}if(ld == -1){sort(nums.begin(), nums.end(), greater<int>());}return nums; } };
上一個全排列算法——third
class Solution { public:/*** @param nums: An array of integers* @return: An array of integers that's previous permuation*/vector<int> previousPermuation(vector<int> &nums) { int n = nums.size();for(int i=n-1; i>=0; --i)for(int j=n-1; j>i; --j)if(nums[i] > nums[j]){swap(nums[i], nums[j]);sort(nums.begin()+i+1, nums.end(), greater<int>());return nums;}sort(nums.begin(), nums.end(), greater<int>());return nums;} };
得到所有全排列算法
lintcode鏈接:http://www.lintcode.com/zh-cn/problem/permutations/
全排列算法——first
注:非遞歸,由下一個全排列算法——third方法實現
class Solution { public:/*** @param nums: A list of integers.* @return: A list of permutations.*/vector<vector<int> > vv;vector<vector<int> > permute(vector<int> nums) {if(nums.size() == 0) return vv;sort(nums.begin(), nums.end());//方法1: 非遞歸實現int n = nums.size();bool flag = true;vv.push_back(nums);while(flag){flag = false;for(int i=n-1; i>=0; --i){for(int j=n-1; j>i; --j)if(nums[i] < nums[j]){swap(nums[i], nums[j]);sort(nums.begin()+i+1, nums.end());vv.push_back(nums);flag = true;break;}if(flag) break;}} return vv;} };
全排列算法——second
class Solution { public:/*** @param nums: A list of integers.* @return: A list of permutations.*/vector<vector<int> > vv;vector<vector<int> > permute(vector<int> nums) {if(nums.size() == 0) return vv;sort(nums.begin(), nums.end()); //方法2:調用<algorithm>中的next_permutation()do{vv.push_back(nums);}while(next_permutation(nums.begin(), nums.end())); return vv;} };
全排列算法——third
注:遞歸思路:一共有nn個位置,然后每個位置枚舉可能出現的數字(注意處理重復數字的情況)
class Solution { public:/*** @param nums: A list of integers.* @return: A list of permutations.*/vector<vector<int> > vv; /// int nn;//沒有 unique 之前的數組的大小map<int, int> mp; void dfs_1(int cur, vector<int> &v, vector<int> nums){if(cur >= nn){vv.push_back(v);return;}for(int i=0; i<nums.size(); ++i)if(mp[nums[i]]){//如果nums[i]這個數字沒有枚舉完--mp[nums[i]];v.push_back(nums[i]);dfs_1(cur+1, v, nums);v.pop_back();++mp[nums[i]];}} //// vector<vector<int> > permute(vector<int> nums) {if(nums.size() == 0) return vv;sort(nums.begin(), nums.end()); //方法3:遞歸for(int i=0; i<nums.size(); ++i)//統計每個重復元素的個數++mp[nums[i]];nn = nums.size();unique(nums.begin(), nums.end());//對數組進行去重vector<int> v;dfs_1(0, v, nums); return vv;} };
全排列算法——forth
注:遞歸思路:每一個數,不斷的和后面的數交換位置,每交換一次就會得到一個新的排列
class Solution { public:/*** @param nums: A list of integers.* @return: A list of permutations.*/vector<vector<int> > vv;void dfs_2(int ld, int rd, vector<int> nums){if(ld == rd){vv.push_back(nums);return ;}for(int i=ld; i<=rd; ++i){swap(nums[ld], nums[i]);dfs_2(ld+1, rd, nums);swap(nums[ld], nums[i]);}}vector<vector<int> > permute(vector<int> nums) {if(nums.size() == 0) return vv;sort(nums.begin(), nums.end()); dfs_2(0, nums.size()-1, nums);return vv;} };
排列序號(按字典序排序屬于第幾個全排列)
注:不含重復數字的排列!
lintcode鏈接:http://www.lintcode.com/zh-cn/problem/permutation-index/
樣例
例如,排列[1,4,2]是第2個全排列。
排列序號算法
算法思想請參考:http://www.cnblogs.com/hujunzheng/p/5020211.html
class Solution { public:/*** @param A an integer array* @return a long integer*/long long permutationIndex(vector<int>& A) {//一個一個來肯定會超時// vector<int> permu(A.begin(), A.end());// sort(permu.begin(), permu.end());// int cnt = 0;// do{// int i;// for(i=0; i<A.size(); ++i)// if(A[i]!=permu[i])// break;// ++cnt;// if(i>=A.size()) break;// }while(next_permutation(permu.begin(), permu.end()));// return cnt; vector<int> a;int len = A.size();int cnt[len];cnt[len-1] = 0;a.push_back(A[len-1]);for(int i=len-2; i>=0; --i){//統計每個數后面有多少個比它小的數的個數vector<int>::iterator it = lower_bound(a.begin(), a.end(), A[i]);cnt[i] = it-a.begin();a.insert(it, A[i]);}long long ans=1, fac=1, c=1;for(int i=len-2; i>=0; --i)ans += (fac*=c++)*cnt[i];return ans;} };
第k個排列
注:給定?n?和?k,求123..n組成的排列中的第?k?個排列。
lintcode鏈接:http://www.lintcode.com/zh-cn/problem/permutation-sequence/
樣例
對于?n = 3, 所有的排列是:123, 132, 213, 231, 312, 321.
如果?k = 4, 第4個排列為,231.
康托展開的公式?:
X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0!,ai為整數,并且0<=ai<i(1<=i<=n)
適用范圍:沒有重復元素的全排列
例題:
找出第16個n = 5的序列(12345)。康托展開只要O(n)就行?,下面來說說具體怎么做:
根據第一行的那個全排列公式,15 / 4! = 0 …15 ?=> ?有0個數比它小的數是1,所以第一位是1
拿走剛才的余數15,用15 / 3! = 2 …3 ? => ?剩下的數里有兩個數比它小的是4(1已經沒了),所以第二位是4
拿走余數3, 用 3 / 2! = 1 …1 ? => ?剩下的數里有一個數比它小的是3,所以第三位是3
拿走余數1, 用 1/ ?1! = 1 …0 ? ?=> ?剩下的數里有一個數比它小的是 5(只剩2和5了),所以第四位是5
所以排列是 1,4,3,5,2
第k個排列算法
?
class Solution { public:/*** @param n: n* @param k: the kth permutation* @return: return the k-th permutation*/string getPermutation(int n, int k) {if(n==1) return "1";int f[n+1];bool use[n+1];f[1] = 0;f[2] = 1;memset(use, false, sizeof(use));for(int i=3; i<=n; ++i)f[i] = f[i-1]*(i-1);string ans = "";--k;//要計算的排列之前有多少個排列for(int i=n; i>=2; --i){int cnt = 0;int c = k/f[i];//假設該排列的這位數是x,c就是比x小的數(之前沒有用過)的個數k%=f[i];for(int j=1; j<=n; ++j){//尋找符合要求的x的值if(!use[j]){if(cnt == c){ans += j+'0';use[j] = true;break;}++cnt;}}}for(int j=1; j<=n; ++j)if(!use[j]){ans += j+'0';break;}return ans;} };
?
帶重復元素的排列
題目鏈接:http://www.lintcode.com/zh-cn/problem/permutations-ii/
帶重復元素的排列——first
思路:next_permutation()本身支持帶重復元素的全排列
class Solution { public:/*** @param nums: A list of integers.* @return: A list of unique permutations.*/vector<vector<int> > ans;vector<vector<int> > permuteUnique(vector<int> &nums) {// write your code here sort(nums.begin(), nums.end());do{ans.push_back(nums);}while(next_permutation(nums.begin(), nums.end()));
return ans;} };
?
帶重復元素的排列——second
思路:枚舉每個位置肯能出現的數字。
class Solution { public:/*** @param nums: A list of integers.* @return: A list of unique permutations.*/vector<vector<int> > ans;map<int, int> cnt;//記錄每個數字在nums中出現的次數 void dfs(int n, vector<int> &nums, vector<int> &v){if(v.size() >= n){ans.push_back(v);return ;}for(int i=0; i<nums.size(); ++i)if(cnt[nums[i]]){--cnt[nums[i]];v.push_back(nums[i]);dfs(n, nums, v);v.pop_back();++cnt[nums[i]];}}vector<vector<int> > permuteUnique(vector<int> &nums) {// write your code here sort(nums.begin(), nums.end());for(int i=0; i<nums.size(); ++i)++cnt[nums[i]];int n = nums.size();nums.erase(unique(nums.begin(), nums.end()), nums.end());//清除重復的元素vector<int> v;dfs(n, nums, v);return ans;} };
?
帶重復元素的排列——third
思路:和 “全排列算法——first”方法類似,唯一不同的是下面代碼中紅色部分。
class Solution { public:/*** @param nums: A list of integers.* @return: A list of unique permutations.*/vector<vector<int> > ans;vector<vector<int> > permuteUnique(vector<int> &nums) {// write your code here sort(nums.begin(), nums.end()); bool flag = true;while(flag){flag = false;ans.push_back(nums);for(int i=nums.size()-1; i>=0; --i){for(int j=nums.size()-1; j>i; --j)if(nums[i] < nums[j]){flag = true;while(j-1>i && nums[j-1]==nums[j]) --j;//如果前面有相同的數字,找到最左邊的數字 swap(nums[i], nums[j]);sort(nums.begin()+i+1, nums.end());break;}if(flag) break;}}return ans;} };
?

)
)


)












)
