01.歐幾里德算法（Euclidean algorithm）（輾轉相除法）

歐幾里德算法又稱輾轉相除法，主要是用于計算兩個整數a,b的最大公約數。

簡單點說一下算法原理：兩個整數的最大公約數等于其中小的那個數跟大除以小余數的最大公約數。

即： gcd(a,b)=gcd(b,a mod b) 。

舉個簡單的例子：

比如求 10跟 24 的最大公約數

a = gcd(10, 24):

1.求10和24的最大公約數等于求10跟4的最大公約數 ：a = gcd(10, 24) = gcd(10, 4)

2.求10跟4的最大公約數等于求4跟2的最大公約數，為2：

a = gcd(10, 24) = gcd(10, 4) = gcd(4, 2) = 2

02.拓展歐幾里德算法

算法原理：若a和b為正整數，則存在整數x, y 使得gcd(a,b)=ax+by;

通俗點說就是 gcd(a,b)可以表示為a,b的整數線性組合。

舉個簡單的例子：

gcd(10, 24) = 2

2 = 10*(-7) + 24*3

主要應用有以下三方面：

1. 求解不定方程；

例題：求 435x + 783y = 87 的一組整數解：

先通過歐幾里得算法得：

783 = 1× 435 + 348

435 = 348×1 + 87

348 = 87 × 4

∴ 87 = 435 – 348

87 = 435 – (783 – 435)

87 = (–1)(783) + 2(435)

∴ x = 2, y = ?1是此不定方程的一組整數解。

2. 求解模的逆元(乘法逆元)，參考上一篇 同余方程、歐拉函數、乘法逆元、定義在Zm上的矩陣求逆

3. 求解模線性方程（線性同余方程）；

1)求解同余方程 ax ≡ b (mod m), x = ?

舉個極端代表性的例子:

15x = 1 mod 26

這道題轉化成15x - 26y = 1 既可以當做1求解不定方程 ,也可以當做2求乘法逆元

解法如下：

26 = 1× 15 + 11

15 = 11×1 + 4

11 = 4 × 2 + 3

4 = 1 × 3 + 1

3 = 1 × 3

∴ 1 = 4 – 3

= 4 – (11 – 4×2)

= 4×3 – 11

= (15-11) ×3 - 11

= 15×3 - 11×4

= (26-11)×3 - 11 ×4

= 26×3 - (26 - 15)×7

=26×(-4) + 15×7

∴ x = 7, y = ?4 為此不定方程的一組整數解，15關于模26的乘法逆元為7

求解同余方程組 繼續往下看中國剩余定理

03.中國剩余定理

在《孫子算經》中有這樣一個問題：“今有物不知其數，三三數之剩二（除以3 余2），

五五數之剩三（除以5 余3），七七數之剩二（除以7 余2），問物幾何？”

宋朝數學家秦九韶于1247年《數書九章》卷一、二《大衍類》對“物不知數”問題做出了完整系統的解答。明朝數學家程大位將解法編成易于上口的《孫子歌訣》：

三人同行七十稀，

五樹梅花廿一支，

七子團圓正半月，

除百零五便得知。

意思是只要是除以3余了一個1，就加上一個70；

只要是除以5余了一個1，就加上一個21；

只要是除以7余了一個1，就加上一個15。然后累加。

最后計算這個總和除以105的余數。

也就是：

(2×70 + 3×21 + 15×2 ) mod 105 = 23

解法如下：

先從3和5、3和7、5和7的公倍數中相應地找出分別被7、5、3除均余1的較小數15、21、70 ( 此步又稱為求"模逆"運算，參考乘法逆元解法)。即：

15÷7=2……余1，

21÷5=4……余1，

70÷3=23……余1.

再用找到的三個較小數分別乘以所要求的數被7、5、3除所得的余數的積連加，

15×2+21×3+70×2=233.

最后用和233除以3、5、7三個除數的最小公倍數.

233÷105=2……余23，

這個余數23就是合乎條件的最小數.

拓展到一般情況：

假設整數m1, m2, ... , mn兩兩互質，則對任意的整數：a1, a2, ... , an 方程組:

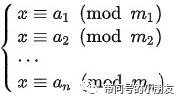
都存在整數解，且若X , Y 都滿足該方程組，則必有 X ≡ Y (mod N) 其中：

公式如下：

課本上的公式符號實在不想看，就拿作業來舉兩個例子吧。

04.作業1：

求解同余方程組：

x ≡ 12 (mod 25)

x ≡ 9 (mod 26)

x ≡ 23 (mod 27)

以上方程組等價于

x = 25a + 12 = 26b + 9 = 27c + 23

移一下項 得：

① : 25a - 27c = 23-12 = 11

②: 26b - 25a = 12-9 = 3

首先對①式運用拓展歐幾里得：

27 = 25×1 + 2

25 = 2×7 + 11

則：

11 = 25 - 2×7

= 25 - (27-25) ×7

= 25×8 - 27×7

所以a=8, c=7

代入x = 25a + 12 = 27c + 23 得：

x = 212

得到合并方程 x = 212 + 25 × 27t 即：x ≡ 212 (mod 675)

然后再跟x ≡ 9 (mod 26) 合并

x = 212 + 675t = 26b + 9

26b - 675t = 203

675 = 26×25+25

25 = 25×1

所以：

203 = (26-25)×203

= (26 - (675-26*25))×203

= 26×5278 - 675×203

b=5278 , t=203

代入得x = 137237

得到合并方程 x = 137237 + 25 × 27×26t 即：x ≡ 137237 (mod 17550) , x=14387

x = 14387 + 17550n (n∈Z）

05.作業2：

求解如下同余方程組：

13x ≡ 4 (mod 99)

15x ≡ 56 (mod 101)

這類同余方程組帶著系數讓人頭大，但是也不妨礙使用拓展歐幾里德，

首先去掉系數：

x ≡ 46 (mod 99)

x ≡ 98 (mod 101)

求解方法很多，這里列舉利用二元一次不定方程方法：

13x ≡ 4 (mod 99) 轉化為 13x-99y = 4

然后用拓展歐幾里德：

13×46-99×6 = 4

x=46, y=6

所以不定方程13x-99y = 4 的所有解為

x=46 + 99t

y=6+13t

所以原同余方程解為：x ≡ 46 (mod 99)

消去x得：99a - 101b = 52

拓展歐幾里德走你：x = 7471 (mod 9999)

x = 9999 n + 7471 (n ∈ Z)

— THE END —