
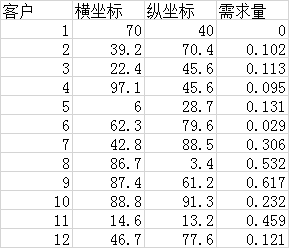
Excel? exp12_3_2.xls內容:
ANT_VRP函數:
function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q)
%% R_best 各代最佳路線
%% L_best 各代最佳路線的長度
%% L_ave 各代平均距離
%% Shortest_Route 最短路徑
%% Shortest_Length 最短路徑長度
%% D 城市間之間的距離矩陣,為對稱矩陣
%% Demand 客戶需求量
%% Cap 車輛最大載重
%% iter_max 最大迭代次數
%% m 螞蟻個數
%% Alpha 表征信息素重要程度的參數
%% Beta 表征啟發式因子重要程度的參數
%% Rho 信息素蒸發系數
%% Q 信息素增加強度系數
n=size(D,1);
T=zeros(m,2*n); %裝載距離
Eta=ones(m,2*n); %啟發因子
Tau=ones(n,n); %信息素
Tabu=zeros(m,n); %禁忌表
Route=zeros(m,2*n); %路徑
L=zeros(m,1); %總路程
L_best=zeros(iter_max,1); %各代最佳路線長度
R_best=zeros(iter_max,2*n); %各代最佳路線
nC=1;
while nC<=iter_max %停止條件
Eta=zeros(m,2*n);
T=zeros(m,2*n);
Tabu=zeros(m,n);
Route=zeros(m,2*n);
L=zeros(m,1);
%%%%%%==============初始化起點城市(禁忌表)====================
for i=1:m
Cap_1=Cap; %最大裝載量
j=1;
j_r=1;
while Tabu(i,n)==0
T=zeros(m,2*n); %裝載量加載矩陣
Tabu(i,1)=1; %禁忌表起點位置為1
Route(i,1)=1; %路徑起點位置為1
visited=find(Tabu(i,:)>0); %已訪問城市
num_v=length(visited); %已訪問城市個數
J=zeros(1,(n-num_v)); %待訪問城市加載表
P=J; %待訪問城市選擇概率分布
Jc=1; %待訪問城市選擇指針
for k=1:n %城市
if length(find(Tabu(i,:)==k))==0 %如果k不是已訪問城市代號,就將k加入矩陣J中
J(Jc)=k;
Jc=Jc+1;
end
end
%%%%%%%=============每只螞蟻按照選擇概率遍歷所有城市==================
for k=1:n-num_v %待訪問城市
if Cap_1-Demand(J(1,k),1)>=0 %如果車輛裝載量大于待訪問城市需求量
if Route(i,j_r)==1 %如果每只螞蟻在起點城市
T(i,k)=D(1,J(1,k));
P(k)=(Tau(1,J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率計算公式中的分子
else %如果每只螞蟻在不在起點城市
T(i,k)=D(Tabu(i,j),J(1,k));
P(k)=(Tau(Tabu(i,visited(end)),J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率計算公式中的分子
end
else %如果車輛裝載量小于待訪問城市需求量
T(i,k)=0;
P(k)=0;
end
end
if length(find(T(i,:)>0))==0 %%%當車輛裝載量小于待訪問城市時,選擇起點為1
Cap_1=Cap;
j_r=j_r+1;
Route(i,j_r)=1;
L(i)=L(i)+D(1,Tabu(i,visited(end)));
else
P=P/(sum(P)); %按照概率原則選取下一個城市
Pcum=cumsum(P); %求累積概率和:cumsum([1 2 3])=1 3 6,目的在于使得Pcum的值總有大于rand的數
Select=find(Pcum>rand); %按概率選取下一個城市:當累積概率和大于給定的隨機數,則選擇求和被加上的最后一個城市作為即將訪問的城市
o_visit=J(1,Select(1)); %待訪問城市
j=j+1;
j_r=j_r+1;
Tabu(i,j)=o_visit; %待訪問城市
Route(i,j_r)=o_visit;
Cap_1=Cap_1-Demand(o_visit,1); %車輛裝載剩余量
L(i)=L(i)+T(i,Select(1)); %路徑長度
end
end
L(i)=L(i)+D(Tabu(i,n),1); %%路徑長度
end
L_best(nC)=min(L); %最優路徑為距離最短的路徑
pos=find(L==min(L)); %找出最優路徑對應的位置:即為哪只螞蟻
R_best(nC,:)=Route(pos(1),:); %確定最優路徑對應的城市順序
L_ave(nC)=mean(L)'; %求第k次迭代的平均距離
Delta_Tau=zeros(n,n); %Delta_Tau(i,j)表示所有螞蟻留在第i個城市到第j個城市路徑上的信息素增量
L_zan=L_best(1:nC,1);
post=find(L_zan==min(L_zan));
Cities=find(R_best(nC,:)>0);
num_R=length(Cities);
for k=1:num_R-1 %建立了完整路徑后在釋放信息素
Delta_Tau(R_best(nC,k),R_best(nC,k+1))=Delta_Tau(R_best(nC,k),R_best(nC,k+1))+Q/L_best(nC);
end
Delta_Tau(R_best(nC,num_R),1)=Delta_Tau(R_best(nC,num_R),1)+Q/L_best(nC);
Tau=Rho*Tau+Delta_Tau;
nC=nC+1;
end
Shortest_Route=zeros(1,2*n); %提取最短路徑
Shortest_Route(1,:)=R_best(iter_max,:);
Shortest_Route=Shortest_Route(Shortest_Route>0);
Shortest_Route=[Shortest_Route Shortest_Route(1,1)];
Shortest_Length=min(L_best); %提取最短路徑長度
%L_ave=mean(L_best);
求解程序:
clc;clear all
%% ==============提取數據==============
[xdata,textdata]=xlsread('exp12_3_2.xls'); %加載20個城市的數據,數據按照表格中位置保存在Excel文件exp12_3_1.xls中
x_label=xdata(:,2); %第二列為橫坐標
y_label=xdata(:,3); %第三列為縱坐標
Demand=xdata(:,4); %第四列為需求量
C=[x_label y_label]; %坐標矩陣
n=size(C,1); %n表示節點(客戶)個數
%% ==============計算距離矩陣==============
D=zeros(n,n); %D表示完全圖的賦權鄰接矩陣,即距離矩陣D初始化
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %計算兩城市之間的距離
else
D(i,j)=0; %i=j, 則距離為0;
end
D(j,i)=D(i,j); %距離矩陣為對稱矩陣
end
end
Alpha=1;Beta=5;Rho=0.75;iter_max=100;Q=10;Cap=1;m=20; %Cap為車輛最大載重
[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q); %蟻群算法求解VRP問題通用函數,詳見配套光盤
Shortest_Route_1=Shortest_Route-1 %提取最優路線
Shortest_Length %提取最短路徑長度
%% ==============作圖==============
figure(1) %作迭代收斂曲線圖
x=linspace(0,iter_max,iter_max);
y=L_best(:,1);
plot(x,y);
xlabel('迭代次數'); ylabel('最短路徑長度');
figure(2) %作最短路徑圖
plot([C(Shortest_Route,1)],[C(Shortest_Route,2)],'o-');
grid on
for i =1:size(C,1)
text(C(i,1),C(i,2),[' ' num2str(i-1)]);
end
xlabel('客戶所在橫坐標'); ylabel('客戶所在縱坐標');



















