一個動態系統的性能常用典型輸入作用下的響應來描述。響應是指零初始值條件下某種典型的輸入函數作用下對象的響應,控制系統常用的輸入函數為單位階躍函數和脈沖激勵函數(即沖激函數)。在MATLAB的控制系統工具箱中提供了求取這兩種輸入下系統響應的函數。
一、時域分析的一般方法
求取系統單位階躍響應:step()
求取系統的沖激響應:impulse()
(一)step()函數的用法
y=step(num,den,t):其中num和den分別為系統傳遞函數描述中的分子和分母多項式系數,t為選定的仿真時間向量,一般可以由t=0:step:end等步長地產生出來。該函數返回值y為系統在仿真時刻各個輸出所組成的矩陣。
[y,x,t]=step(num,den):此時時間向量t由系統模型的特性自動生成,狀態變量x返回為空矩陣。
[y,x,t]=step(A,B,C,D,iu):其中A,B,C,D為系統的狀態空間描述矩陣,iu用來指明輸入變量的序號。x為系統返回的狀態軌跡。
如果對具體的響應值不感興趣,而只想繪制系統的階躍響應曲線,可調用以下的格式:
step(num,den);step(num,den,t);step(A,B,C,D,iu,t);step(A,B,C,D,iu);
線性系統的穩態值可以通過函數dcgain()來求取,其調用格式為:
dc=dcgain(num,den)或dc=dcgain(a,b,c,d)
例exp4_3.m已知系統的開環傳遞函數為:

求系統在單位負反饋下的階躍響應曲線。
clc
clear
closeall
%開環傳遞函數描述
num=[20];
den=[1836400];
%求閉環傳遞函數
[numc,denc]=cloop(num,den);
%繪制閉環系統的階躍響應曲線
t=0:0.1:10;
y=step(numc,denc,t);
[y1,x,t1]=step(numc,denc);
%對于傳遞函數調用,狀態變量x返回為空矩陣
plot(t,y,'r:',t1,y1)
title('thestepresponce')
xlabel('time-sec')
%求穩態值
disp('系統穩態值dc為:')
dc=dcgain(numc,denc)
(二)impulse()函數的用法
求取脈沖激勵響應的調用方法與step()函數基本一致。
y=impulse(num,den,t);[y,x,t]=impulse(num,den);[y,x,t]=impulse(A,B,C,D,iu,t)
impulse(num,den);impulse(num,den,t)
impulse(A,B,C,D,iu);impulse(A,B,C,D,iu,t)
例exp4_4.m已知系統的開環傳遞函數為:

求系統在單位負反饋下的脈沖激勵響應曲線。
clc
clear
close
%開環傳遞函數描述
numo=20;
deno=[1836400];
%求閉環傳遞函數
[numc,denc]=cloop(numo,deno,-1);
%繪制閉環系統的脈沖激勵響應曲線
t=1:0.1:10;
[y,x]=impulse(numc,denc,t);
plot(t,y)
title('theimpulseresponce')
xlabel('time-sec')
仿真時間t的選擇:
對于典型二階系統根據其響應時間的估算公式
 可以確定。
可以確定。
對于高階系統往往其響應時間很難估計,一般采用試探的方法,把t選大一些,看看響應曲線的結果,最后再確定其合適的仿真時間。
一般來說,先不指定仿真時間,由MATLAB自己確定,然后根據結果,最后確定合適的仿真時間。
在指定仿真時間時,步長的不同會影響到輸出曲線的光滑程度,一般不易取太大。
二、常用時域分析函數
時間響應探究系統對輸入和擾動在時域內的瞬態行為,系統特征如:上升時間調節時間超調量和穩態誤差都能從時間響應上反映出來。MATLAB除了提供前面介紹的對系統階躍響應沖激響應等進行仿真的函數外,還提供了大量對控制系統進行時域分析的函數,如:
covar:連續系統對白噪聲的方差響應
initial:連續系統的零輸入響應
lsim:連續系統對任意輸入的響應
對于離散系統只需在連續系統對應函數前加d就可以,如dstep,dimpulse等。
它們的調用格式與stepimpulse類似,可以通過help命令來察看自學。
三、時域分析應用實例
MATLAB的step()和impulse()函數本身可以處理多輸入多輸出的情況,因此編寫MATLAB程序并不因為系統輸入輸出的增加而變得復雜。
例exp4_7.m 某2輸入2輸出系統如下所示:


,求系統的單位階躍響應和沖激響應。
clc
clear
close
%系統狀態空間描述
a=[-2.5-1.2200;1.22000;1-1.14-3.2-2.56;...
002.560];
b=[41;20;20;00];
c=[0103;0001];
d=[0-2;-20];
%繪制閉環系統的階躍響應曲線
figure(1)
step(a,b,c,d)
title('stepresponse')
xlabel('time-sec')
ylabel('amplitude')
figure(2)
impulse(a,b,c,d)
title('impulseresponse')
xlabel('time-sec')
ylabel('amplitude')
例exp4_8.m 某系統框圖如下所示,求d和e的值,使系統的階躍響應滿足:1.超調量不大于40%,2.峰值時間為0.8秒。

由圖可得閉環傳遞函數為:
 ,其為典型二階系統。
,其為典型二階系統。
由典型二階系統特征參數計算公式
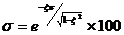 ,
,
 得:
得:
 ,
,
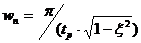
clear
clc
closeall
%輸入期望得超調量及峰值時間
pos=input('pleaseinputexpectpos(%)=');
tp=input('pleaseinputexpecttp=');
z=log(100/pos)/sqrt(pi^2+(log(100/pos))^2);
wn=pi/(tp*sqrt(1-z^2));
num=wn^2;
den=[12*z*wnwn^2];
t=0:0.02:4;
y=step(num,den,t);
plot(t,y)
xlabel('time-sec')
ylabel('y(t)')
grid
d=wn^2
e=(2*z*wn-1)/d



















(草稿))