之前看過高斯過程(GP)，不過當時也沒太看懂，最近花時間認真研究了一下，感覺總算是明白咋回事了，本文基于回歸問題解釋GP模型的思想和方法。文中的想法是自己思考總結得來，并不一定準確，也可能存在錯誤性。
為什么要用GP？
回顧一下我們之前在解決回歸問題時，就拿線性回歸舉例，我們為了學習映射函數，總是把函數參數化，例如假設
，然后計算參數
的后驗分布，把參數估計出來之后，就得到了我們想要學習的函數，接著就可以用這個函數去做預測了。
但是有時候我們并不知道數據到底用什么形式的函數去擬合比較好(是1次的，2次的還是10次的？)。這個時候高斯過程(GP)就閃亮登場了，GP說：“我不需要用參數去刻畫函數，你就告訴我訓練數據是什么，你想要預測哪些數據，我就能給你預測出結果。“這樣一來，我們就省去了去選擇刻畫函數參數的這樣一個過程。
GP是怎么來的？
那么GP是怎么做到的呢？我們先來看這樣一件有趣的事情：
假設我們的函數定義域和值域都是
,那么如果你的訓練集是包含了所有定義域的，那么這個函數
我們就得到了，你給任何一個點，我都能通過查表的方式告訴你結果是多少。第二種情況我們的訓練集中缺少了
這四個點，并且這四個點就是我們需要進行預測的點，如果我們可以通過某種方式建立一個4維的概率分布
，其中
分別代表
的預測值，那么我們是不是就可以就可以利用這個概率分布，找到對應的概率最高的點把最終的結果給估計出來。
然而，事實上雖然很多實際問題（比如房價的預測），它的定義域和值域都是
(或者是某個連續的區間)，但是我們的訓練數據是有限的，而基于這些訓練數據，我們要對整個實數域進行預測，如果我們繼續利用上面的思想的話，我們需要建立一個無窮維度的概率分布（因為我們需要進行預測的數據點事無窮個的），這顯然不可能，不過慶幸的是，在每一次我們需要進行預測的時候，我們所需要進行預測的數據是有限的。假設有N個訓練數據
,有N*個需要進行預測的數據
,
表示
，那么我們最終其實就是希望得到
(
代表了
所有預測值的變量的集合)。
高斯過程(GP)
下面我們就開始正式的介紹高斯過程(GP)，它是怎么得到這個
，然后去做預測的。在GP中，首先基于訓練數據和測試數據，定義了基于定義域
的函數的概率分布
其中
。
是正定的核函數。
代表了
所有預測值的變量的集合。這里有一個關鍵的思想，如果核函數認為兩個輸入是非常相似的，那么函數給出的輸出值也會非常的相似。(在這樣的刻畫中，我們發現
其實好像并沒有太大的作用，事實上，我們通常令
)。這個定義總體給出了三個信息：
- 在本次訓練中，我們的定義域是
。
- 在這個定義域中，如果
基于核函數是非常接近的，那么你們的輸出值也會非常接近。
- 我們是用高斯分布去進行刻畫（用高斯的好處，至少有一點條件概率密度函數很好算）。
我們把上面的概率分布展開：
其中
利用高斯分布的性質（通過聯合分布計算條件分布），我們可以得到
這樣我們計算出了我們希望得到的
。至此為止，整個GP就結束了。關于GP那么它有什么優點呢，我認為有兩點：
- 這一點也是我們上面就說過的，GP是無參的，對于任何一組數據，你不需要知道他的結構是什么，你也不需要去用參數刻畫它函數的樣子，GP就可以幫你做預測。
- GP它刻畫出了函數的概率分布。這個非常有用。回顧之前的線性回歸的方法，當你把參數
估計出來后，你的函數就確定了，接下來我拿出任何一個數，你都會“毫無感情的”給我一個預測值。但是GP不一樣，當我們知道我們預測函數的不確定度（不確定度很高，這個預測的結果就不可靠）之后，我們能探索最不可能實現高效訓練的數據區域。這也是貝葉斯優化背后的主要思想。下面這句話我覺得寫得非常貼切：如果你給我幾張貓和狗的圖片，要我對一張新的貓咪照片分類，我可以
有噪聲觀測的情況下
在有噪觀測的情況下，我們假設觀測模型是這樣的
，其中
，那么觀測的核函數則更新為
（假設不同觀測之間是獨立的），基于這樣的假設，聯合概率分布和條件概率分布分別是：
，
核函數參數的影響
那么核函數對GP有什么影響呢，假設我們選擇SE核函數：
（
表示p=q時取1，否則取0）
這個核函數有三個參數，分別是
，
和
，分別控制著水平尺度，垂直尺度，以及噪聲的方差。通過三幅圖我們來看看這三個參數是怎么控制預測的結果的：
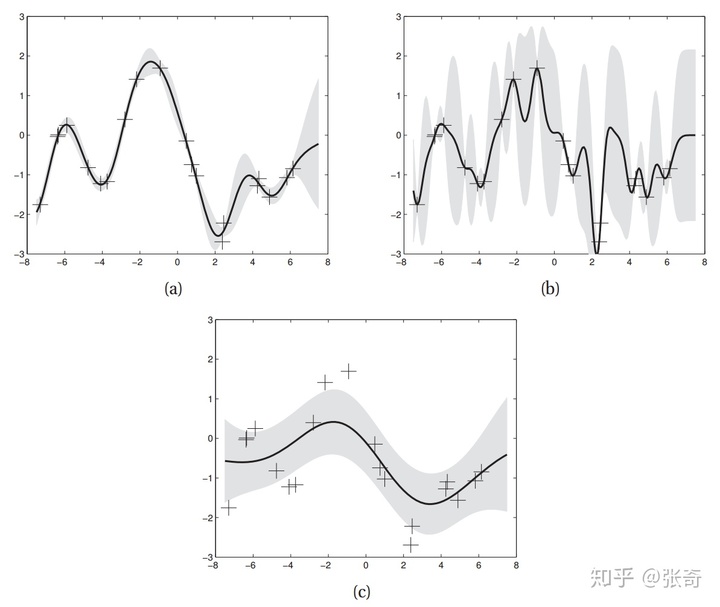
三幅圖的超參數
分別是：
。（只改變
，其他的參數是通過優化邊際似然函數得到的）
我們可以看到（a）圖整體看上去是估計的比較好的，（b）圖中，減小了
,我們發現圖變得彎彎曲曲的，而且一旦預測的數據點稍微遠離訓練的數據點，這個不確定度就大大的上升（因為只要輸入的距離稍微大一點點，核函數就認為它們已經非常不相似了）。（c）圖中，
為3，函數看上去更加的平滑了，但是擬合的效果就顯得很差。
有什么作用？)
