導讀:本文將介紹在廣告行業中自然語言處理和推薦系統實踐。本文主要分享從理論到實戰知識蒸餾,對知識蒸餾感興趣的小伙伴可以一起溝通交流。
摘要:本篇主要分享從理論到實戰知識蒸餾。首先講了下為什么要學習知識蒸餾。一切源于業務需求,BERT這種大而重的模型雖然效果好應用范圍廣,但是很難滿足線上推理的速度要求,所以需要進行模型加速。通常主流的模型加速方法主要包括剪枝、因式分解、權值共享、量化和知識蒸餾等;然后重點講解了知識蒸餾,主要包括知識蒸餾的作用和原理、知識蒸餾的流程以及知識蒸餾的效果等;最后理論聯系實戰,講解了實際業務中主要把BERT作為老師模型去教作為學生模型的TextCNN來學習知識,從而使TextCNN不僅達到了媲美BERT的分類效果,而且還能很好的滿足線上推理速度的要求。對知識蒸餾感興趣的小伙伴可以一起溝通交流。
下面主要按照如下思維導圖進行學習分享:
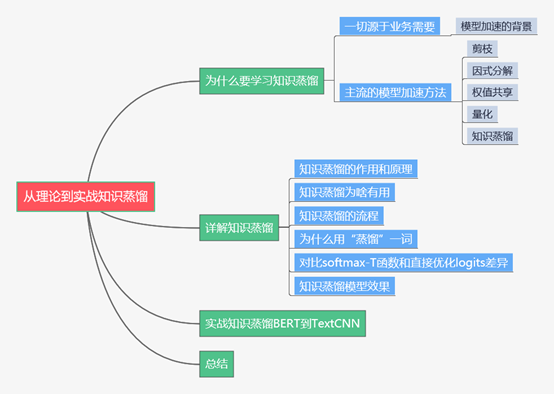
01 為什么要學習知識蒸餾
1.1 一切源于業務的需要
目前大火的BERT這一類預訓練+微調的兩階段模型因為效果好和應用范圍廣在各種自然語言處理任務中瘋狂屠榜取得state-of-art。在線下時延較低的場景下這類模型可以很好的滿足業務需求,但是在線上推理場景中比如用戶實時搜索返回廣告就很難滿足時延要求。實際業務中我們線上的文本推理時延需求是在10ms以內,因為模型太大(BERT基礎版本有330M接近一億的參數量)所以似乎很難滿足線上推理的要求。
現在我們面臨這樣一種困境:BERT這類大模型精度高但是線上推理速度慢,傳統的文本分類模型比如TextCNN等線上推理速度快(因為模型比較小)但是精度有待提升。針對上面的問題,我們的需求是獲得媲美BERT等大模型的精度,還能滿足線上推理速度的時延要求。
1.2 主流的模型加速方法
明確了我們的目標是獲得大模型高精度的同時還能很好的滿足線上推理的速度要求,這就需要用到模型加速技術。目前主流的模型加速方法主要有以下幾種:
剪枝。對模型的網絡進行修剪,比如減掉多余的頭(因為Transformer使用多頭注意力機制),或者直接粗暴的使用更少的Transformer層數;
因式分解。之前比較火的ALBERT模型使用的一個優化策略就是對embedding參數進行因式分解。因為BERT將詞向量和encode輸出的維度都設置為768維,而encode中包含豐富的語義信息,所以明顯存儲的信息量比詞向量多,所以ALBERT的策略就是采用因式分解的方法把詞向量映射到低維空間,這樣就能大大降低參數量,最后再映射回高維的embedding向量;
權值共享。這也是ALBERT中使用的優化策略之一。對Transformer各層參數可視化分析發現各層參數類似,都是在[CLS]token和對角線上分配更多的注意力,通過多層之間共享參數從而達到了模型加速的目的。對ALBERT中因式分解和全職共享感興趣的小伙伴可以轉過頭來看看我之前寫的這篇文章《廣告行業中那些趣事系列6:BERT線上化ALBERT優化原理及項目實踐(附github)》
量化。量化操作主要是以精度換速度,業界也有嘗試在BERT微調階段進行量化感知訓練,使用最小的精度損失將BERT模型參數壓縮了4倍。這些量化操作方案很多也是為了將模型移植到移動端進行的優化;
知識蒸餾。知識蒸餾是把大模型或者多個模型ensemble學到的知識想辦法遷移到一個輕量級的小模型上去,線上部署這個小模型就可以了。
之前在知乎上看到過有好心人整理了主流模型加速的論文分享,下面是論文分類圖片,有興趣的小伙伴可以多看看論文:
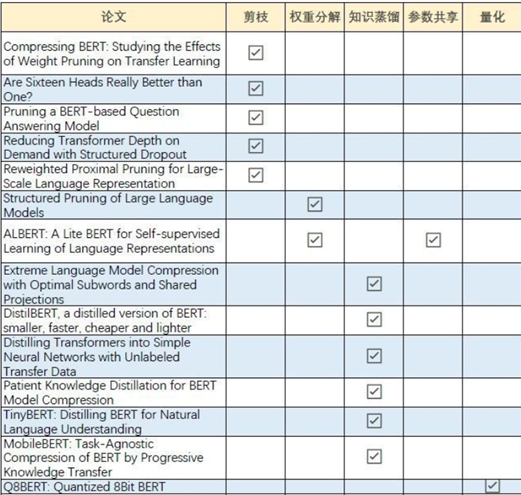
02 詳解知識蒸餾
2.1 知識蒸餾的作用和原理
要搞明白知識蒸餾的作用,咱們還是拿前面的例子來說明。BERT這一類模型優點在于效果好,但是如果用于線上推理就比較麻煩了,因為基礎版本的BERT模型接近330M包含一億的參數,你想讓一個一億參數的模型完成線上10ms內的線上推理基本有點不現實。而傳統的文本分類算法比如TextCNN可以輕松滿足線上推理的需求,但是效果相比BERT還是有點不如人意。知識蒸餾通俗的理解就是BERT當老師,TextCNN當學生,讓BERT這個老師把學到的知識傳授給TextCNN這個學生,這樣就能讓TextCNN達到和BERT媲美的效果,最后我們線上去部署TextCNN,就能做到模型效果和線上推理速度兼得。這就是知識蒸餾的作用。
知識蒸餾的概念最早是2015年Geoffrey Hinton在《Distilling the Knowledge in a Neural Network》這篇論文中提出來的。知識蒸餾就是把一個大模型或者多個模型ensemble學到的知識遷移到另一個輕量級的單模型上,最主要的目的是為了方便線上部署。從上面的概念中也可以看出知識蒸餾主要有兩個方面:第一個是將大而深的模型遷移到一個輕量級的小模型上。這就像我們線上把大而深的BERT模型學到的知識遷移到輕量級的TextCNN小模型上;另一個就是將多個模型ensemble學到的知識遷移到單個輕量級的模型。多個模型ensemble的操作在kaggle比賽中非常常見,為了提升那1到2個百分點,各種花里胡哨奇淫巧計無所不用其極。但是在工業場景中倒沒有那么普遍,畢竟生產場景是要考慮投入產出比的。你得時刻掂量花了那么多時間精力以及機器算力提升的那一點點精度是不是真的劃得來。而知識蒸餾就可以把多個模型ensemble學到的知識通通學到手,真正的做到集百家之長。
一點反思,感覺知識蒸餾和讀書很像。一些人經歷過各種酸甜苦辣學到了很多有用的知識,這些人就像老師模型一樣。他們會通過寫書等方式把這些知識傳承下來,這時候我們可以通過讀書(知識蒸餾)來學習他們的知識,就算不用去經歷他們的酸甜苦辣我們照樣能用學到的知識去指導我們以后的生活,相當于我們得到了“老師”的泛化能力。
2.2 知識蒸餾為啥有用
眾所周知,一個好的模型最重要的是通過訓練數據獲得一定的泛化能力,不僅僅是擬合訓練數據,最重要的是在新數據集上能有一定的泛化識別能力。而知識蒸餾的目的是讓學生去學習老師的這種泛化能力,所以從理論上來說學生比老師單純的去擬合訓練數據能獲得更多的知識。下面通過手寫數據集的例子來說明知識蒸餾為啥能學到更多的知識:
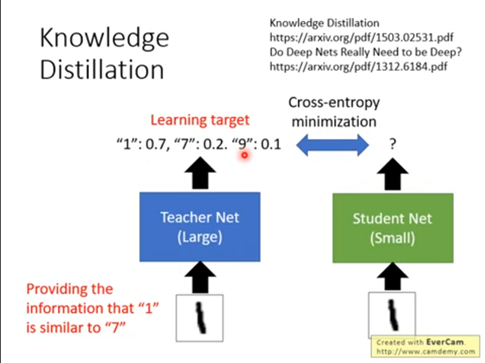
對于老師或者沒有使用知識蒸餾的小模型來說,主要是通過訓練數據來學習知識。我們的訓練數據集是一張一張手寫數字的圖片,還有對應0到9十個數字的標簽。在這種學習中我們可以用的只有十個類別值,比如一張手寫數字1的圖片樣本的標簽是1,告訴模型的知識就是這個樣本標簽是1,不是其他類別。而使用知識蒸餾的時候模型可以學到更多的知識,比如手寫數字1的圖片樣本有0.7的可能是數字1,0.2的可能是數字7,還有0.1的可能是數字9。這非常有意思,模型不僅學到了標簽本身的知識,還學習到了標簽之間的關聯知識,就是1和7、9可能存在某些關聯,這些知識稱為暗知識,這是知識蒸餾學到的知識,也是知識蒸餾有用的重要原因。
2.3 知識蒸餾的流程
知識蒸餾主要如圖所示包括以下幾個流程:

首先,訓練一個老師模型。這里的老師模型可以是大而深的BERT類模型,也可以是多個模型ensemble集成后的模型。因為這里沒有線上推理的速度要求,所以主要目標就是提升效果;
然后,設計蒸餾模型的loss函數訓練學生模型,這也是最重要的步驟。蒸餾模型的loss函數定義如下:
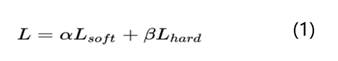
蒸餾模型的loss函數主要分成兩部分:L_soft和L_hard。其中L_soft是老師教學生學習的損失函數,L_hard是學生自己跟著答案(標簽)學習的損失函數,a和b(貝塔打不出來)一般相加為1。
再看看老師是怎么教學生學習的,L_soft公式具體如下圖所示:
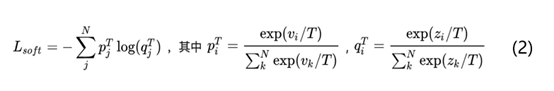
上述公式中p代表老師模型的輸出結果,然后將老師模型的輸出結果p作為學生模型的目標,使學生模型的輸出結果q盡可能接近p,具體就是計算老師和學生的交叉熵。這里重點是T的作用,T是知識蒸餾里的超參數,論文中稱為溫度temperature。分類任務中一般采用的就是softmax+交叉熵的模型,當T=1時其實就是softmax函數。如果老師模型直接使用softmax函數輸出結果p可能不太合適,主要原因是當一個模型訓練好之后對于正確的答案一般會有很好的置信度。就像上面講的手寫數據集中圖片樣本1被預測為數字1的概率會很高,同時預測為其他數字的概率也會很低,比如10e-5等等。這樣的情況下老師模型很難將學到的標簽類型之間聯系的知識傳遞給學生模型。
針對這個問題,知識蒸餾的作者提出了softmax-T函數,也就是通過temperature來控制老師模型輸出的結果p的分布。p是學生模型學習的對象,v_i就是模型softmax前的輸出logits。當T=1的時候這個公式就是softmax,根據logits輸出各個類別的概率;當T接近0時,概率最大的類別輸出值就會接近1,其他的輸出值接近0,作用類似one-hot編碼;當T越大時,會使各個類別輸出的概率分布相對平緩,從而一定程度上保留了各個類別之間的聯系知識;極端情況下,當T趨于無窮大時概率分布會變成一個均勻分布。溫度T對softmax-T函數的概率分布影響如下圖所示:

綜合來說知識蒸餾通過控制超參數T使得老師模型的輸出概率分布會保留類別之間的聯系知識。個人覺得這也是知識蒸餾模型中最重要的知識點。
下面是L_hard損失函數公式:

L_hard其實和常規模型是一樣的,就是根據訓練集的label來學習。上面公式中c就是正確答案label,也就是計算學生模型的輸出結果q和標簽c的交叉熵。
L_soft和L_hard分別對應的是樣本soft target和hard target。下面通過手寫數字集樣本1來對比 soft target和hard target的區別:
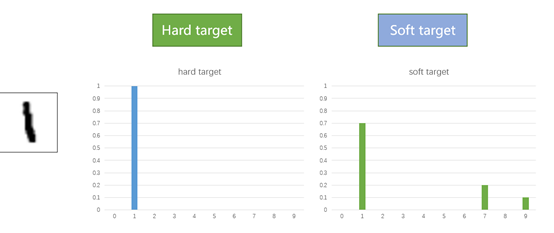
通過上圖可以發現Hard target中樣本的分布比較“極端”,是0或者1,而Soft target中樣本的分布會更加平滑一些。
最后是使用學生模型進行線上預測。這里需要注意線上預測的時候需要把T設置回1。
2.4 為什么用“蒸餾”一詞
知識蒸餾的目的是讓學生模型的softmax輸出結果q盡可能的接近老師模型的softmax輸出結果p。一般的softmax函數中指數e會把logits之間的差距拉大,然后作歸一化,使得最終得到的分布是arg max的近似,也就是其中一個類別值很大,其他類別值非常小,類似one-hot,這樣使老師模型無法把標簽之間的聯系知識教給學生,也就是上面說的手寫數字1的圖片樣本它有0.7的可能是數字1,0.2的可能是數字7,還有0.1的可能是數字9這樣的暗知識沒有辦法傳遞給學生模型。為了讓老師模型softmax輸出的結果分布更平滑一些,最簡單直接的做法是直接比較logits。比如z_i是學生模型產生的logits,v_i是老師模型產生的logits,其實就是最小化v_i和z_i:
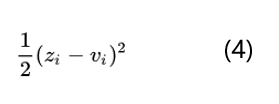
針對這個問題知識蒸餾的作者提出了softmax-T函數。這里的T是溫度temperature,是統計力學中的概念。前面也說過當T趨于0時softmax的輸出結果會接近one-hot編碼,也就是一個類別值接近1,其他類別接近0;當T趨向于無窮的時候,softmax的輸出會趨向于均勻分布。
利用這個特性我們會在訓練學生分類器的時候設置較高的T使得softmax輸出的結果具有一定的平滑性,作用自然是學習類別之間的聯系知識,也讓學生模型的輸出盡可能接近老師模型。當學生模型訓練完成之后再把T設置為1來進行線上預測。
之所以叫“蒸餾”也是和化學中的蒸餾概念接近。化學中通過蒸餾的方法可以把不同沸點的物質區分開,流程就是升溫把低沸點的物質汽化,然后迅速降溫冷凝從而達到分離物質的目的。對比下知識蒸餾的概念也是這樣,學生模型訓練時增加溫度參數T,然后在線上預測的時候降低溫度T為1從而將老師模型中的知識提取出來,這和化學中的蒸餾流程非常類似。這可能也是作者命名為知識蒸餾的一個原因吧。
2.5 對比softmax-T函數和直接優化logits差異
上面也說過知識蒸餾中最有價值的就是通過softmax-T使得老師模型的softmax輸出結果包含類別之間聯系的暗知識,所以這里咱們再深入了解下softmax-T和直接優化logits也就是公式4之間的差異。學生模型訓練時我們需要最小化老師分布和學生分布的交叉熵,下面是最小化交叉熵的公式:
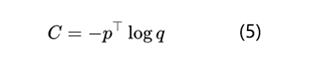
根據公式2和公式5,計算學生模型交叉熵對某個logits分布z_i的梯度就是:
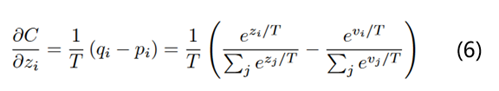
回顧點高數知識,當x趨于0的時候,exp(x)-1和x是等價無窮小的。也就是說當T無窮大的時候,就變成了如下的公式:
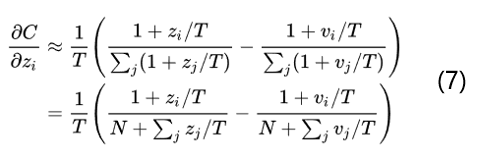
當所有的logits對每個樣本都是零均值化時, z_j的求和=v_j的求和=0,那么就變成了如下的公式:
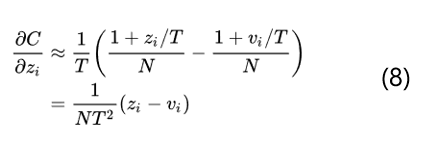
得到了公式8就可以看出當T足夠大并且logits對所有樣本都是零均值化的時候知識蒸餾和最小化logits的平方差也就是公式4是等價的。所以總體來說通過softmax-T不僅和最小化logits是等價的,而且還可以通過控制超參數T來調節老師模型的輸出結果分布,具有很好的靈活性。
2.6 知識蒸餾模型效果
知識蒸餾模型的作者主要進行了以下三個實驗:
第一個實驗是驗證可以將大而深的模型知識轉移到小模型上。在MNIST數據集上先使用大而深的模型進行訓練,測試集中有67個錯誤;然后使用小模型進行訓練,測試集中有146個錯誤;最后使用知識蒸餾的方法在目標函數中加入L_soft,學生模型在測試集中錯誤變成了74個。通過這個實驗可以看出知識蒸餾的確可以使學生模型獲得老師模型的知識從而提升小模型的效果。有趣的是作者還發現即使在訓練集中不包含某一類的訓練數據,通過知識蒸餾的方法在測試集中竟然能識別到沒有包含這一類標簽的數據。也就是說在訓練集中可能學生模型從來沒見過3,但是在測試集中竟然有識別3的能力。厲害不?
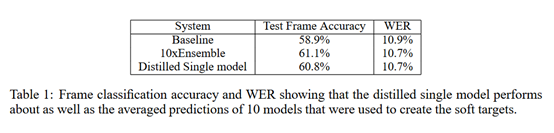
第二個實驗主要是驗證將多個模型ensemble得到的知識轉移到單一模型上。在語音識別任務中首先訓練了10個DNN模型,然后通過ensemble的方式得到最終的模型,經過ensemble得到的模型效果是優于任意單個模型的;然后將這10個DNN模型作為老師模型去訓練學生模型,得到的學生模型效果是優于任意一個老師模型的,可以看出經過知識蒸餾得到的學生模型的確學習到了老師模型的知識。下面是詳細實驗結果:
03 實戰知識蒸餾BERT到TextCNN
實際業務中我們線下場景因為沒有時延的要求所以主要使用BERT模型來完成文本分類任務。而對于線上推理任務分別嘗試了FastBERT、ALBERT等等貌似都達不到10ms的時延要求,目前主要使用知識蒸餾的方法來進行模型加速。將BERT作為老師模型,把 TextCNN作為學生模型來學習老師的知識。按照目前的實驗效果來看,TextCNN學到了BERT的知識,在測試集和真實分布數據集上的效果良好,推理速度也是滿足時延的。
構造TextCNN代碼如下:
class TextCNN(object): """ 利用bert作為teacher,指導textcnn學習logits,損失函數為KL散度 """ def __init__( self, sequence_length, vocab_size, embedding_size, filter_sizes, num_filters,dropout_keep_prob=0.2): self.dropout_keep_prob = dropout_keep_prob # Placeholders for input, output self.input_x = tf.placeholder(tf.int32, [None, sequence_length], name="input_x") self.labels = tf.placeholder(tf.int32, shape=None, name="labels") self.teacher_logits = tf.placeholder(tf.float32, shape=None, name="teacher_logits") # Embedding layer # with tf.device('/cpu:0'), tf.name_scope("embedding"): with tf.name_scope("embedding"): self.W = tf.Variable( tf.random_uniform([vocab_size, embedding_size], -1.0, 1.0), name="W") self.embedded_chars = tf.nn.embedding_lookup(self.W, self.input_x) self.embedded_chars_expanded = tf.expand_dims(self.embedded_chars, -1) # Create a convolution + maxpool layer for each filter size # textcnn模型結構 pooled_outputs = [] for i, filter_size in enumerate(filter_sizes): with tf.name_scope("conv-maxpool-%s" % filter_size): # Convolution Layer filter_shape = [filter_size, embedding_size, 1, num_filters] W = tf.Variable(tf.truncated_normal(filter_shape, stddev=0.1), name="W") b = tf.Variable(tf.constant(0.1, shape=[num_filters]), name="b") conv = tf.nn.conv2d( self.embedded_chars_expanded, W, strides=[1, 1, 1, 1], padding="VALID", name="conv") h = tf.nn.relu(tf.nn.bias_add(conv, b), name="relu") # Maxpooling over the outputs pooled = tf.nn.max_pool( h, ksize=[1, sequence_length - filter_size + 1, 1, 1], strides=[1, 1, 1, 1], padding='VALID', name="pool") pooled_outputs.append(pooled) # Combine all the pooled features num_filters_total = num_filters * len(filter_sizes) self.h_pool = tf.concat(pooled_outputs, 3) self.h_pool_flat = tf.reshape(self.h_pool, [-1, num_filters_total]) # Add dropout with tf.name_scope("dropout"): self.h_drop = tf.nn.dropout(self.h_pool_flat, self.dropout_keep_prob) l2_loss = tf.constant(0.0) num_classes = 2 # Final (unnormalized) scores and predictions with tf.name_scope("output"): W = tf.get_variable( "W", shape=[num_filters_total, num_classes], initializer=tf.contrib.layers.xavier_initializer()) b = tf.Variable(tf.constant(0.1, shape=[num_classes]), name="b") l2_loss += tf.nn.l2_loss(W) l2_loss += tf.nn.l2_loss(b) self.scores = tf.nn.xw_plus_b(self.h_drop, W, b, name="scores")[:,1] self.logits = tf.nn.softmax(self.scores) tf.add_to_collection("logits", self.logits) with tf.name_scope("loss"): loss = 0.1*tf.nn.softmax_cross_entropy_with_logits(logits=self.logits, labels=self.labels) loss = tf.reduce_sum(loss) self.loss = loss + 0.9*tf.keras.losses.KLDivergence()(tf.nn.log_softmax(self.scores), self.teacher_logits) 





)












