前面兩篇博客介紹了線性表的順序存儲與鏈式存儲以及對應的操作,并且還聊了棧與隊列的相關內容。本篇博客我們就繼續聊數據結構的相關東西,并且所涉及的相關Demo依然使用面向對象語言Swift來表示。本篇博客我們就來介紹樹結構的一種:二叉樹。在之前的博客中我們簡單的聊了一點樹的東西,樹結構的特點是除頭節點以外的節點只有一個前驅,但是可以有一個或者多個后繼。而二叉樹的特點是除頭結點外的其他節點只有一個前驅,節點的后繼不能超過2個。
本篇博客,我們只對二叉樹進行討論。在本篇博客中,我們對二叉樹進行創建,然后進行各種遍歷,最后將二叉樹進行線索化。在Demo實現之前,我們先對二叉樹的概念及其特性進行介紹,然后在給出具體的代碼實現。
?
一、二叉樹的特性
上面我們已經提到過,一個除頭結點外,每個節點只有一個前驅,有零到兩個后繼的樹即為二叉樹。在二叉樹中,一個節點可以有左節點或者左子樹,也可以有右節點或者右子樹。一些特殊的二叉樹,比如斜二叉樹、滿二叉樹、完全二叉樹等等就不做過多贅述了。說這么多,不如看一張圖來的直觀。下方就是一個典型的二叉樹。

了解二叉樹,理解其特性還是比較重要的。基于二叉樹本身的邏輯結構,下方是二叉樹這種數據結構所具備的特性。
- 特性1:在二叉樹的第i層上至多有2^(i-1)(i >= 1)個節點。
- 這一特性比較好理解,如果層數是從零開始數的話,那么低i層上的節點數就是2^i,因為二叉樹層與層之間的節點數是以2的指數冪進行增長的。如果根節點算是第0層的話,那么第n層的節點數就是2^n次冪。
- 特性2:深度為k的二叉樹至多有2^k-1(k>=1)個節點。
- 這一特性也是比較好理解的, 由數學上的遞加公式就可以很容易的推出來。由特性1易知每層最多有多少個節點,那么深度為k的話,說明一共有k層,那么共有節點數為:2^0 + 2^1 + 2^2 + 2^(k-1) = 2^k - 1。
- 特性3:二叉樹的葉子節點數為n0, 度為2的節點數為n2, 那么n0 = n2 + 1。
- 這一特性也不難理解,推出n0 = n2 + 1這個公式并不難。我們假設葉子節點,也就是度數為0的節點的個數為n0, 度數為1的節點為n1, 度數為2的節點n2。那么二叉樹的節點總數?n = n0 + n1 + n2。因為除了根節點外其余的節點入度都為1,所以二叉樹的度數為n-1,當然度的個數可以使用出度來算,即為2*n2+n1,所以n-1=2*n2+n1。以n=n0+n1+n2與n-1=2*n2+n1這兩個公式我們很容易的推出n0 = n2 + 1。
- 特性4:具有n個結點的完全二叉樹的深度為log2n + 1?(向下取整,比如3.5,就取3)。
- 這個特性也是比較好理解的,基于完全二叉樹的特點,我們假設完全二叉樹的深度為k, 那么二叉樹的結點個數的范圍為2(k-1)-1 <= n <= 2k-1。由這個表達式我們很容易推出特性4。
二、二叉樹的創建
上面介紹完二叉樹的特性后,接下來我們要做的就是將二叉樹進行存儲。當然一般存儲二叉樹的結構是以二叉鏈表的形式來存儲的。二叉鏈表的結構類似于雙向鏈表,二叉鏈表的節點也是有兩個結點指針的,一個指向左子樹,一個指向右子樹。接下來我們要使用二叉鏈表的形式來存儲我們的二叉樹。
?
1.先序創建二叉樹
在創建二叉樹之前,我們先了解一個什么是先序遍歷。先序遍歷就是先遍歷根結點,然后遍歷左子樹,最后遍歷右子樹。我們就以此規則來創建二叉樹,換句話說,我們有一個數據序列,將依照這個序列按照先序創建二叉樹的原則來創建該二叉樹,先創建二叉樹的根節點,然后再創建二叉樹的左子樹,然后再創建右子樹。而這個創建的二叉樹的先序遍歷的結果就是我們之前輸入的數據序列。下方就是先序創建二叉樹的原理圖。
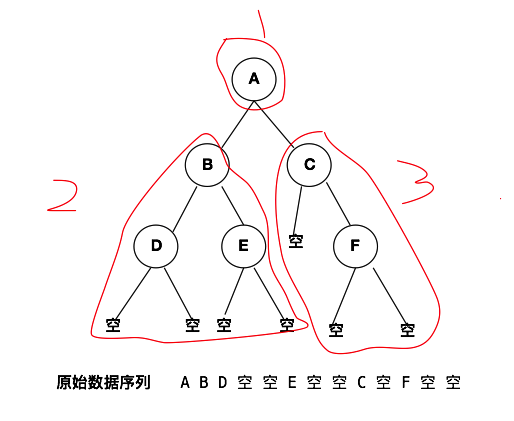
從上面的分析我們不難看出,我們要先創建根節點,然后創建左子樹,最后創建右子樹。因為左子樹和右子樹都是二叉樹,所以創建左子樹和右子樹是原問題的子問題。也就是說子問題與原問題解決方案一致,這種情況下就可以使用遞歸的思想來解決。我們先將上述二叉樹的結構轉換成二叉鏈表的形式直觀的感受一下,然后再將其使用代碼的形式進行表示即可。下方這個截圖就是上述二叉樹的二叉鏈表的存儲結構。每個節點都有左指針與右指針,分別自己的左子節點和右子節點。如果沒有子節點就為空。

2.先序創建二叉樹的代碼實現
上面我們分析了二叉鏈表的結構,接下來我們就來創建二叉鏈表了。首先我們得創建二叉鏈表的節點類,之前我們用C語言來實現二叉樹的時候,是使用的結構體來實現的二叉鏈表的節點,因為C語言是面向過程的語言,根本就沒有類這個概念。因為此刻我們是使用的面向對象語言,所以我就可以使用一個類來表示我們二叉鏈表的節點了。下方這個GeneralBinaryTreeNote就是二叉鏈表的類。data屬性存儲的就是樹節點中所存儲的值,而leftChild就指向左節點的內存地址,而rightChild就指向右節點的內存地址。
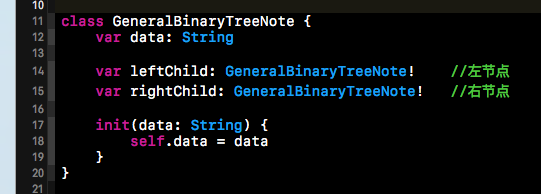
上面我們已經說過,先序創建二叉樹的過程是可以用遞歸來表示的,所以我們就遞歸的去創建我們想要創建的二叉樹。下方就是先序創建二叉樹的核心代碼,self.items中存儲的是二叉樹的節點信息。經過下方函數的遞歸執行,就可以創建出我們想要的二叉樹了。從下方的遞歸過程我們就明顯的能看出是先序創建的二叉樹。先創建的根節點,然后遞歸創建左子樹,然后在遞歸創建右子樹。
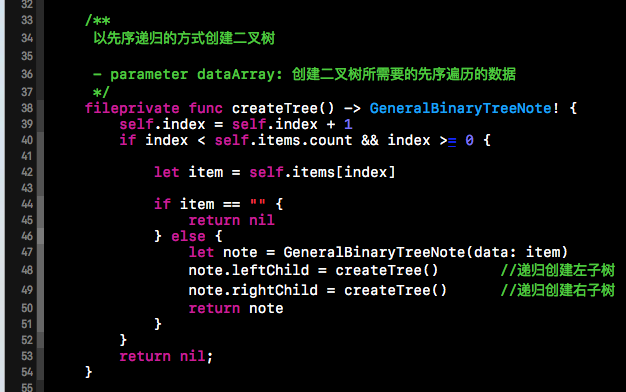
下方就是我們二叉樹的初始化過程,下方在初始化過程中主要是調用上方的這個方法,將items數組中存儲的值轉換成二叉鏈表的存儲結構。items數組中的空字符串,表明該節點為空。
![]()
其實上面實例中所創建的二叉樹的結構就是下方的結構。

?
三、二叉樹的遍歷
聊二叉樹怎么能沒有二叉樹的遍歷呢,下方就會給出幾種常見的二叉樹的遍歷方法。在遍歷二叉樹的方法中一般有先序遍歷,中序遍歷,后續遍歷,層次遍歷。本篇博客主要給出前三種遍歷方式,而層次遍歷會在圖的部分進行介紹。二叉樹的層次遍歷其實與圖的廣度搜索是一樣的,所以這部分放到圖的相關博客中介紹。下方會給出幾種遍歷的具體方式,然后給出具體的代碼實現。
二叉樹的先、中、后遍歷,這個先中后指的是遍歷根節點的先后順序。先序遍歷:根左右,中序遍歷:左根右,后序遍歷:左右根。下方將詳細介紹到。
?
1.先序遍歷
關于先序遍歷,上面已經介紹過一些了,接下來再進行細化一下。先序遍歷,就是先遍歷根節點然后再遍歷左子樹,最后遍歷右子樹。下圖就是我們上面創建的二叉樹的先序遍歷的順序,由下方的示例圖就可以看出先序遍歷的規則。一句話總結下方的結構圖:根節點->左節點->右節點。下方先序遍歷的順序為:A B D?空?空?E?空?空?C?空?F?空?空?。

上面給出了原理,接下來又到了代碼實現的時候了。在樹的遍歷時,我們依然是采用遞歸的方式,因為無論是左子樹還是右子樹,都是二叉樹的范疇。所以在進行二叉樹遍歷時,可以使用遞歸遍歷的形式。而先序遍歷莫非就是先遍歷根節點,然后遞歸遍歷左子樹,最后遍歷右子樹。下方就是先序遍歷的代碼實現。在下方代碼中,如果左節點或者右節點為空,那么我們就輸出“空”。
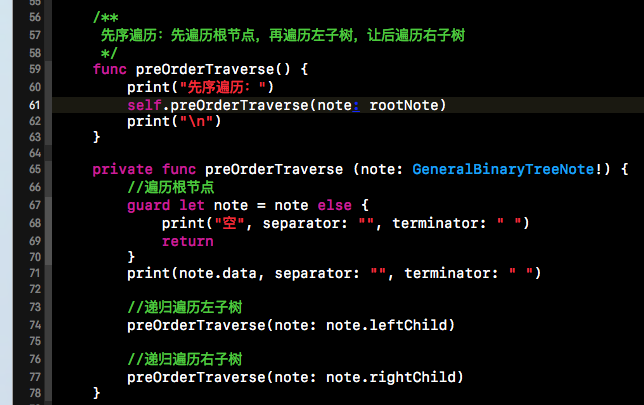
?
2.中序遍歷
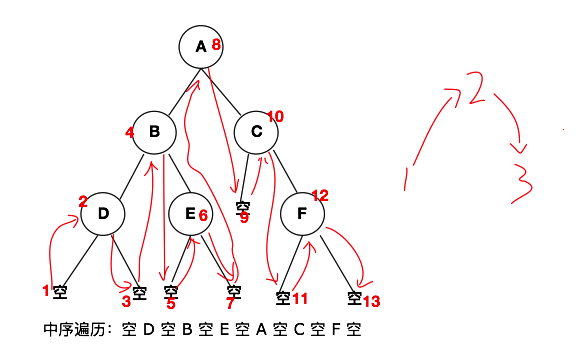
中序遍歷,與先序遍歷的不同之處在于,中序遍歷是先遍歷左子樹,然后遍歷根節點,最后遍歷右子樹。一句話總結:左子樹->根節點->右子樹。下方就是我們之前創建的樹的中序遍歷的結構圖以及中序遍歷的結果。
 ?
?
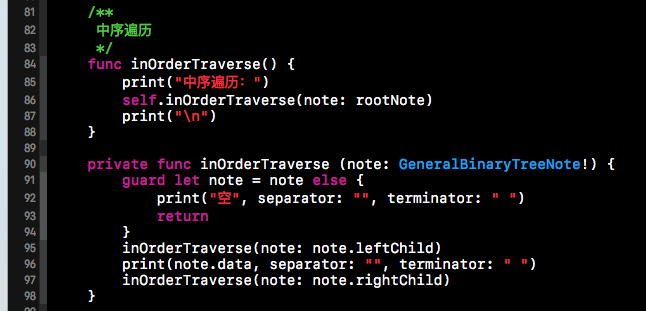
中序遍歷的代碼實現與先序遍歷的代碼實現類似,都是使用遞歸的方式來實現的,只不過是先遞歸遍歷左子樹,然后遍歷根節點,最后遍歷右子樹。下方就是中序遍歷的代碼具體實現。
?
3.后序遍歷
接下來聊一下二叉樹的后序遍歷。如果上面這兩種遍歷方式理解的話,那么后序遍歷也是比較好理解的。后序遍歷是先遍歷左子樹,然后再遍歷右子樹,最后遍歷根節點。與上方的表示方法一直,首先我們給出表示圖,如下所示:
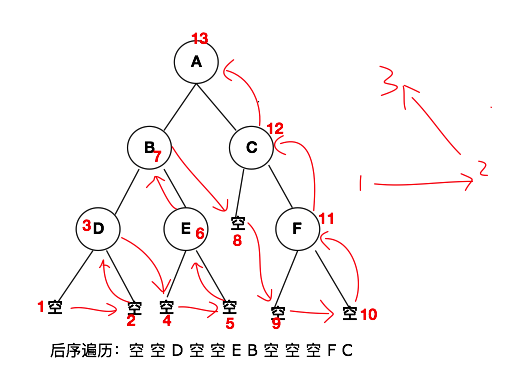
后序遍歷的代碼就不做過多贅述了,與之前兩種依然類似,只是換了一下遍歷的順序。下方就是二叉樹后序遍歷的代碼實現。
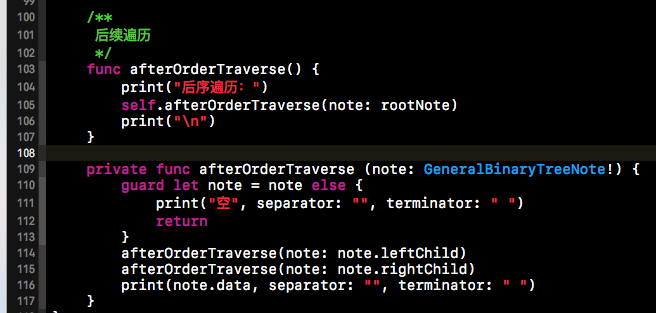
?
4、層次遍歷
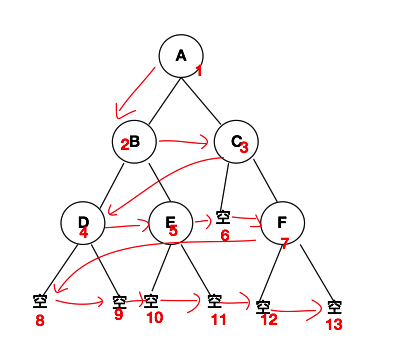
二叉樹的層次遍歷就不是二叉樹這種數據結構所獨有的了。后面的博客中我們會介紹到圖這種數據結構,在圖中有一個廣度搜索,放到二叉樹中就是層次遍歷。也就是說二叉樹的層次遍歷,就是圖中以二叉樹的根節點為起始節點的廣度搜索(BFS)。本篇博客就不給出具體的代碼了,后面的博客會給出BFS的具體算法。當然在之前的博客中有圖的BFS以及DFS。不過是C語言的實現。下方就是二叉樹層次遍歷的實例圖。
?
四、二叉樹的線索化
二叉樹的線索化,起始就是利用二叉樹中的空的節點來將二叉樹轉換成鏈表的結構。當然只針對中序遍歷的序列。從上面中序遍歷的結果中,我們不難看出,有節點的值與空指針是間隔的(空?D?空?B?空?E?空?A?空?C?空?F?空)。也就是說好多空的左指針與右指針浪費了。二叉樹的線索化,就是在中序遍歷中,將空的左子樹的指針指向其中序遍歷結果的前驅,而空的右子樹指針指向中序遍歷中該節點的后繼。具體的示意圖如下所示:
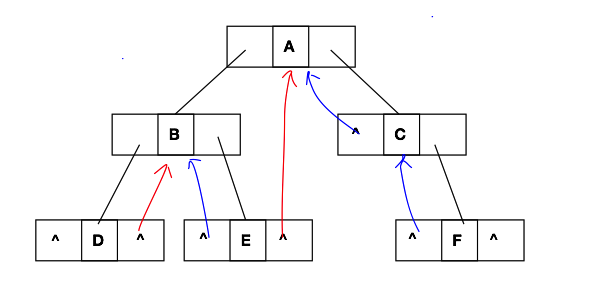
從上面的圖中我們不難看出。在被線索化的二叉樹中,左節點指針不止指向左節點,而且有可能指向節點的前驅。而右節點指針不僅僅是指向右節點的指針,還有可能指向該節點在中序遍歷中的后繼節點。為了標記指針是指向子節點還是指向前驅或者后繼,所以我們要添加相應的標志位來標記指針指向的是那些節點。下方就是我們改造后的二叉樹的節點:
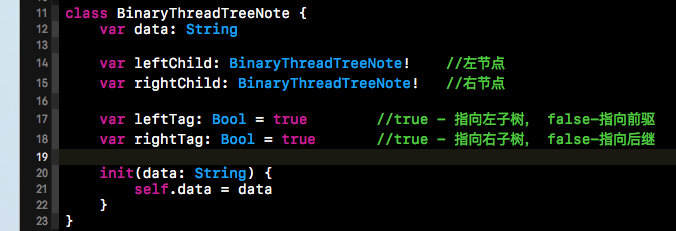
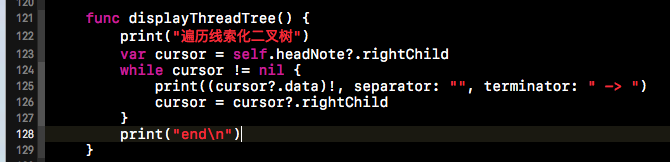
改造完節點后,我們就可以將二叉樹進行線索化了,下方就是被線索話的二叉樹的代碼。可以看出,下方的代碼的整體步驟與二叉樹的中序遍歷類似。
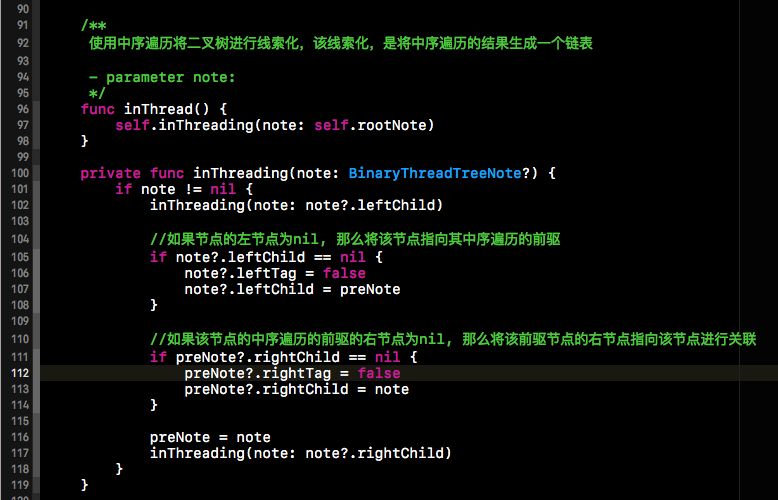
被線索化的二叉樹就可以根據我們添加的線索進行中序遍歷了,效率要比遞歸的中序遍歷要高的多,如下所示:
?
五、測試用例
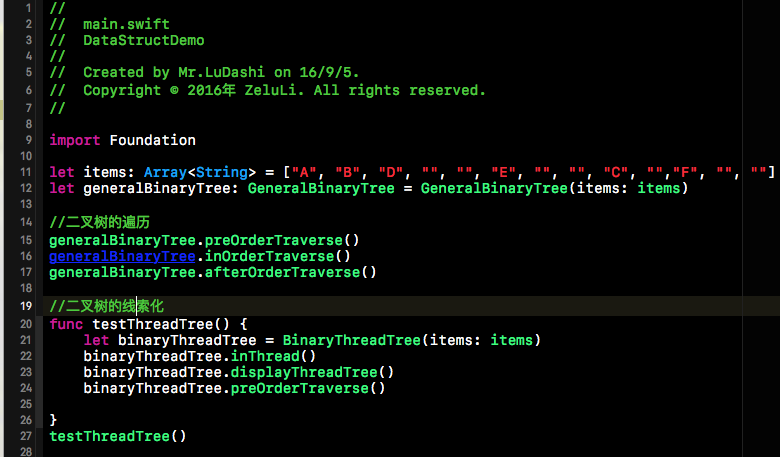
上面的代碼都是如何去實現了,接下來到了我們測試的時間了,下方這段代碼段是我們的測試用例。首先給出二叉樹的節點信息,然后先序的創建一棵二叉樹。然后給出二叉樹的先、中、后續遍歷,最后給出二叉樹線索話的結果。
 ?
?
下方截圖就是我們測試用例的運行結果,一目了然,在此就不做過多的贅述了。
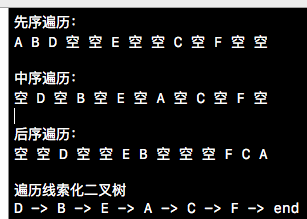
本篇博客的篇幅也夠長的了,就先到這兒吧,上述實例的完整Demo會在github上進行分享, 下篇博客我們將要介紹圖的鄰接鏈表和鄰接矩陣,以及圖的BFS和DFS。
github鏈接地址:https://github.com/lizelu/DataStruct-Swift/tree/master/BinaryTree
?





系統調用的原子性 - 堆棧內存溢出...)







函數時無法找到已創建的R.layout的布局文件的的問題的解決辦法)
——配置攔截器)

)


