學過SVM后，看了那么多別人的文章，是時候自己總結一波了。權當寫的筆記供自己日后再回顧吧。
PS:結合自己在工作過程中（我這里用SVR做股票預測）用到的知識來寫的，不會很全面，若有些知識這里沒提及讀者可自行查找。
1 概述
支持向量機(support vector machine)是一種分類算法，但是也可以做回歸，根據輸入的數據不同可做不同的模型（若輸入標簽為連續值則做回歸，若輸入標簽為分類值則用SVC()做分類）。通過尋求結構化風險最小來提高學習機泛化能力，實現經驗風險和置信范圍的最小化，從而達到在統計樣本量較少的情況下，亦能獲得良好統計規律的目的。通俗來講，它是一種二類分類模型，其基本模型定義為特征空間上的間隔最大的線性分類器，即支持向量機的學習策略便是間隔最大化，最終可轉化為一個凸二次規劃問題的求解。

SVM算法的優缺點：
SVM算法優點區
? 可用于線性/非線性分類，也可以用于回歸；
? 低泛化誤差；
? 容易解釋；
? 計算復雜度較低；
? 可以解決高維問題；
缺點區
? 對參數和核函數的選擇比較敏感；
? 原始的SVM只比較擅長處理二分類問題；
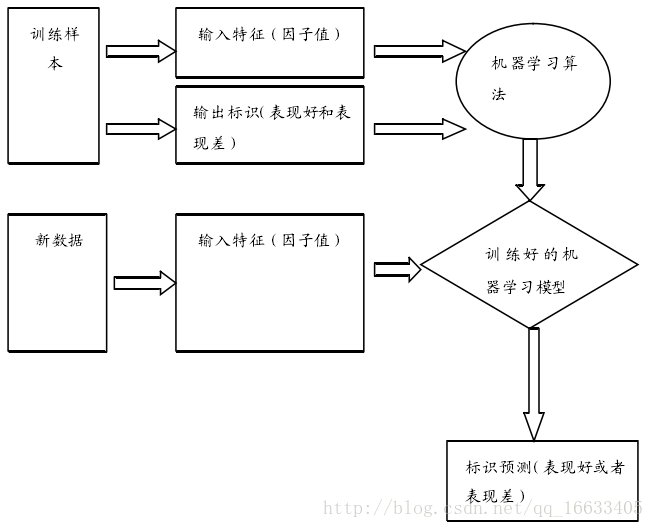
SVM屬于監督學習算法，監督學習流程如圖所示：

2 算法原理
2-1 在n維空間中找到一個分類超平面，將空間上的點分類。如下圖是線性分類的例子。

圖 2-1-1 線性分類的例子
2-2. 一般而言，一個點距離超平面的遠近可以表示為分類預測的確信或準確程度。SVM就是要最大化這個間隔值。而在虛線上的點便叫做支持向量Supprot Verctor。如圖4-1-1-2所示：

圖2-1-1-2 支持向量的標識圖
2-3. 實際中，我們會經常遇到線性不可分的樣例，此時，我們的常用做法是把樣例特征映射到高維空間中去如圖4-1-1-3所示：

圖2-1-1-3 對于線性不可分數據的處理方法
3 數據處理
preprocessing.scale()作用：
scale()是用來對原始樣本進行縮放的，范圍可以自己定，一般是[0,1]或[-1,1]。
縮放的目的主要是
1）防止某個特征過大或過小，從而在訓練中起的作用不平衡；
2）為了計算速度。因為在核計算中，會用到內積運算或exp運算，不平衡的數據可能造成計算困難。

4 SVR參數選擇
對于SVM算法，我們首先導入sklearn.svm中的SVR模塊。SVR()就是SVM算法來做回歸用的方法（即輸入標簽是連續值的時候要用的方法），通過以下語句來確定SVR的模式（選取比較重要的幾個參數進行測試。隨機選取一只股票開始相關參數選擇的測試）。
svr = SVR(kernel=’rbf’, C=1e3, gamma=0.01)

4-1. kernel:核函數的類型，一般常用的有’rbf’，’linear’，’poly’，等如圖4-1-2-1所示，發現使用rbf參數時函數模型的擬合效果最好。

圖4-1-2-1 函數參數“Linear”,“RBF”,“Poly”對模型的擬合效果圖”

4-2. C:懲罰因子。C表征你有多么重視離群點，C越大越重視，越不想丟掉它們。C值大時對誤差分類的懲罰增大，C值小時對誤差分類的懲罰減小。當C越大，趨近無窮的時候，表示不允許分類誤差的存在，margin越小，容易過擬合；當C趨于0時，表示我們不再關注分類是否正確，只要求margin越大，容易欠擬合。如圖4-1-2-2所示發現當使用1e3時最為適宜。

圖 4-1-2-2 參數C與準確度的關系圖

4-3. gamma: 是’rbf’，’poly’和’sigmoid’的核系數且gamma的值必須大于0。隨著gamma的增大，存在對于測試集分類效果差而對訓練分類效果好的情況，并且容易泛化誤差出現過擬合。如圖4-1-2-3所示發現gamma=0.01時準確度最高。

圖4-1-2-3 參數gamma與準確度的關系圖

以上大概就是就是建立股票預測模型的整個過程，在這里重點講的還是算法中各個方法的作用和各主要參數代表的含義，希望對大家有所幫助。