1、知道LDA的特點和應用方向

1.1、特點

知道LDA說的降維代表什么含義：將一篇分詞后的文章降維為一個主題分布（即如20個特征向量主題）。
根據對應的特征向量中的相關主題概率（20個主題的概率相加為1即為主題分布）得到對應的文檔主題，屬于無監督學習（你沒有給每個數據打標簽）

1.2、應用方向

信息提取與搜索（語義分析），文檔的分、聚類，文章摘要，計算機視覺，生物信息等方向（只要包含隱變量都可考慮使用）

PS：知道樸素貝葉斯在文本分析的劣勢：無法識別一詞多義和多詞一意。

2、知道Beta分布和Dirichlet分布數學含義

Beta分布概率密度表達式是一條曲線，系數B的表達式是曲線下的面積。

知道二項分布的共軛先驗分布是Beta分布，多項分布的共軛先驗分布是Dirichlet分布。

知道Dirichlet分布的概率密度函數的數學含義:當K=3時，密度函數數學含義也就是一個曲面

3、了解共軛先驗分布

含義：找個一個先驗分布和后驗分布都滿足于同一種分布的概率分布。這樣你知道其中的一個分布就代表知道了另外一個分布。

4、知道先驗概率和后驗概率

**先驗概率:**是指根據以往經驗和分析得到的概率.
**后驗概率:**事情已經發生，要求這件事情發生的原因是由某個因素引起的可能性的大小

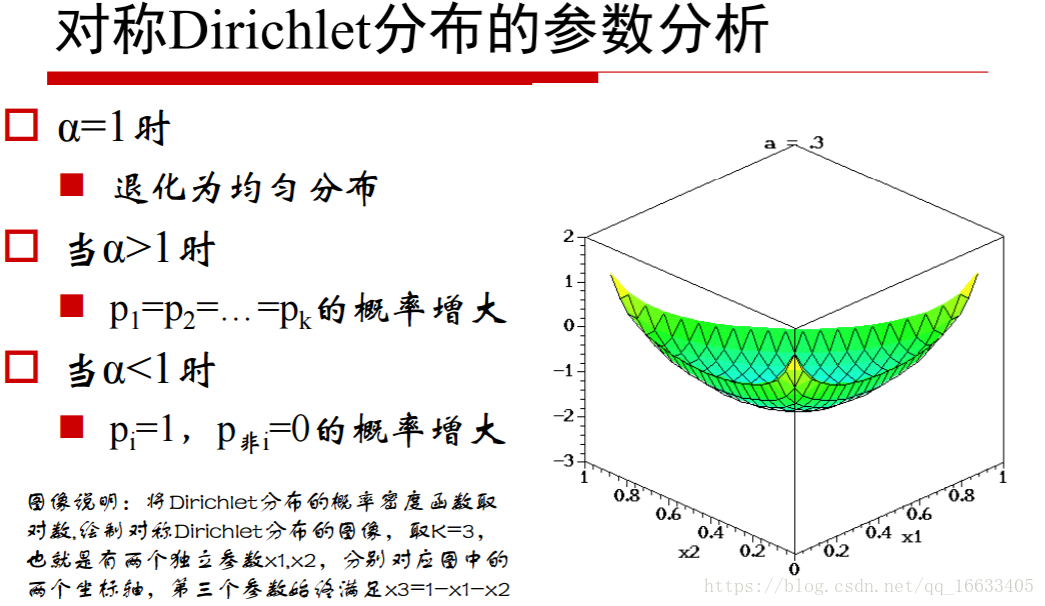
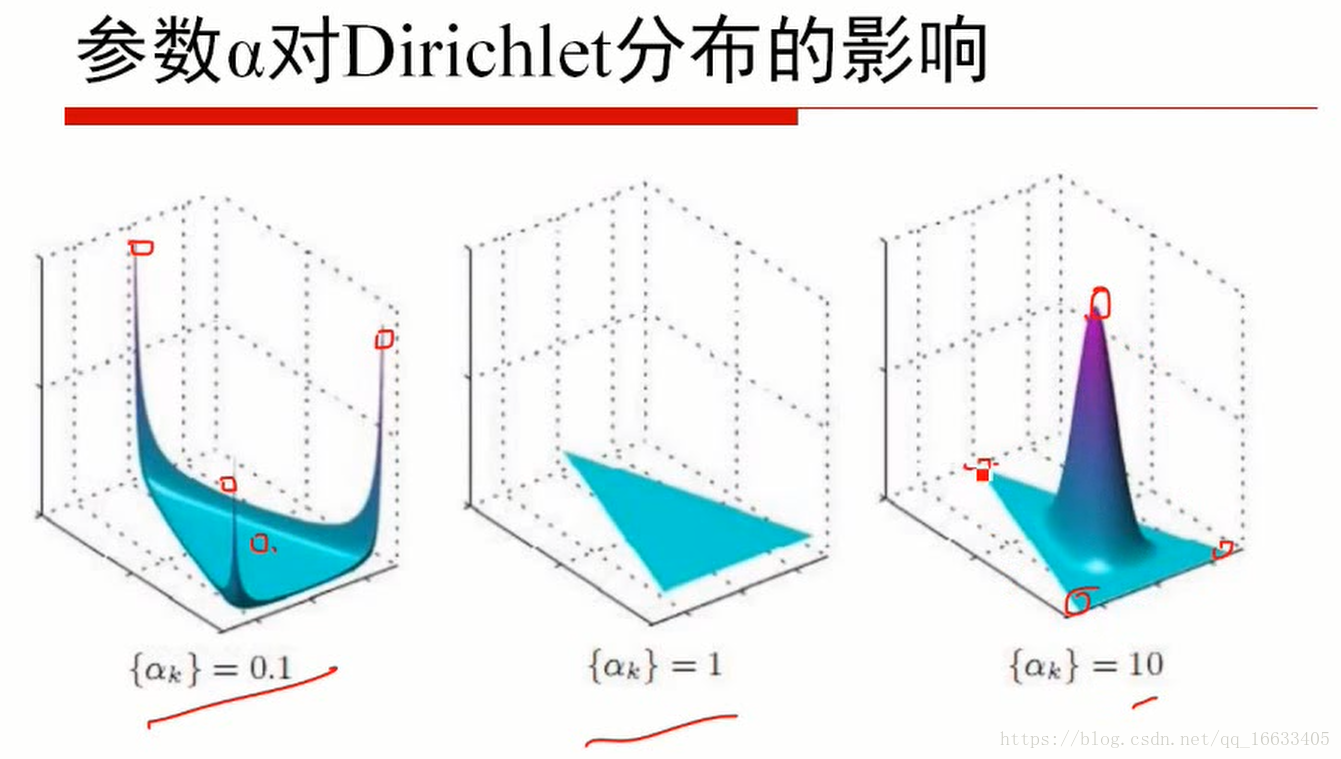
5、知道參數α值的大小對應的含義

當α小于1的時候代表取某一個值的概率很高（即某一主題的概率很高即主題鮮明），=1的時候代表概率為均勻分布，大于1的時候代表k個p相同的概率增大。
對應的z軸就代表這個點對應的概率

6、掌握LDA主題模型的生成過程

總結一句話：主題概率模型生成一個主題分布再生成一個主題，詞概率模型生成主題的詞分布再生成一個詞；最終得到一個主題對應這個詞。（連接的條件主題的標號）


掌握整個過程：
θ代表的一個主題分布，即K維的主題向量。

1. 從α控制的Dirichlet分布的概率密度函數中采取一個對應的K維的主題分布即θm（第m篇文檔的主題）
2. 從β控制的Dirichlet分布的概率密度函數中生成K個對應的V維的詞分布即φk
3. Zm,n即代表第m個文檔的第n個主題。當n=2時即代表采到第m篇文檔的第二個主題，就到對應的β生成的第二個主題的詞分布即φk（對應的第幾個主題的詞分布）
4. 從φk中隨機挑選一個詞作為Wm,n的值（即第m篇文檔第n個主題對應的詞）
5. 循環執行上述步驟得到每個主題對應的詞
   
   PS：各個參數的含義
   θm代表第m篇文檔的主題分布（m為文檔總數)
   φk表示第k個主題的詞分布（k為主題的個數）
   Zm,n代表第m篇文檔中的第n個主題
   Wm,n代表第m篇文檔中的第n個單詞

7、知道超參數α等值的參考值

8、LDA總結

• 由于在詞和文檔之間加入的主題的概念，可以較好的解決一詞多義和多詞一義的問題。
• 在實踐中發現，LDA用于短文檔往往效果不明顯一這是可以解釋的：因為一個詞被分配給某個主題的次數和一個主題包括的詞數目尚未斂。往往需要通過其他方親“連接”成長文檔。
• 用戶評論/Twitter/微博囗LDA可以和其他算法相結合。首先使用LDA將長度Ni的文檔降維到K維（主題的數目），同時給出每個主題的概率（主題分布），從而可以使用if-idf繼續分析或者直接作為文檔的特征進入聚類或者標簽傳播算法用于社區發現等問題。
• 知道LDA是一個生成模型，由y得到對應的x（y代表的是主題，x代表的詞）