一、數據類型及操作

#整數類型，和數學中整數的一樣，可正可負

*十進制：210

*二進制：以0B或者0b開頭：0b1010

*八進制：以0O或者0o開頭：0o123

*十六進制：以0x或者0X開頭：0x9a

-示例：pow(2,50)#計算2^50

#浮點數類型，和數學中的實數一樣

*浮點數的取值范圍在-10^307-10^308之間

*浮點數存在不確定位數，這是因為電腦中數據存儲數字是二進制，二進制表示小數可以無限接近，但是永遠不會等于。

-示例：0.1+0.2==0.3 return false；round(0.1+0.2,1)==0.3 return true

-round()函數介紹，它在python里面起到四舍五入的效果，第一個參數是輸入要計算的式子，第二個參數是把式子產生的得數進行幾位小數的保留，例如上面案例中，0.1+0.2=0.3， 此時0.3是保留了1位小數。如果我們把第二個參數省略不寫，那么會默認為四舍五入后為整數，也就是小數位個數為0。由于不確定尾數一般出現在10^-16處，所以采用round()函數很有用。

*使用字母e或者E作為冪的符號，以10為基數。

#復數類型，和數學中的復數類型一樣

*z=a+bj稱為復數，其中，a是實部，b是虛部。

*獲取復數的實部：z.real

*獲取復數的虛部：z.imag

-示例：z=1.2+12j z.real return 1.2 z.imag return 12.0

#數值運算操作符

*x+y 加，x與y之和

*x-y 減，x與y之差

*x*y 乘，x與y之積

*x/y 除，x與y之商

*x//y 整數除

-案例：10//3 return 3

*+x x本身

*-x x的負值

*x%y 余數，模運算，

-案例：10%3 return 1

*x**y 冪運算x^y

*x**=3 與 x=x**3等價（下面類似）

* x*=y

* x-=y

* x*=y

* x/=y

* x//=y

* x%=y

* x**=y

#類型之間可以進行混合運算，生成結果為“最寬”類型

整數->浮點數->復數

-案例:12+4.0=16.0

#運算函數

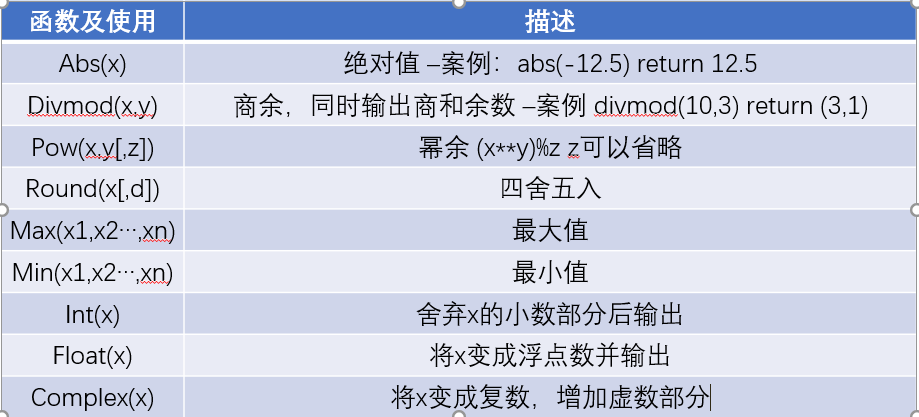
-案例：a=divmod(10,3); a[0] return 3 a[1] return 1

二、字符串類型及操作

#字符串類型的表示

*字符串由一對單引號或一堆雙引號表示

-‘C’

*字符串是字符的有序序列，可以對其中的字符進行索引

-"A" 是字符串 "ABCDEFG"的第0個字符

*一對單引號或者雙引號表示，僅表示單行字符串。

*由一對三單引號或三雙引號表示，可以表示多行字符串（這是為了方便引號的表示）‘

*字符串的序號

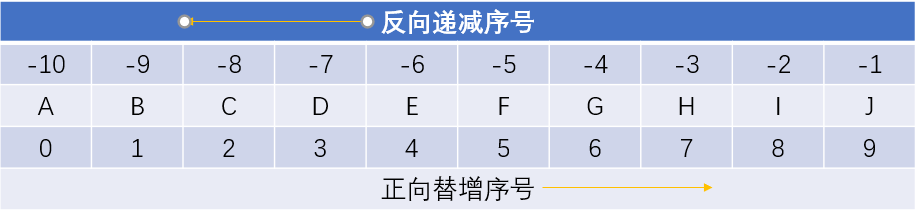
*字符串的使用

索引：返回字符串中單個字符 <字符串>[M]

切片：返回字符串中一段字符字串 <字符串>[M:N]（注意：它不包含索引為N的那一項）

-其中，<字符串>[M:N],M缺失表示從N至開頭，N缺失表示從M至結尾

-<字符串>[M:N:K] 根據步長K對字符串切片：-案例:"ABCDEFG"[1:8:2] return “BDF”

轉義字符：“\b” 回退 "\n" 換行 "\r" 回車 "這里有一個引號(\')" return “這里有一個引號(')”

#字符串操作符

#字符串處理函數

#字符串處理方法

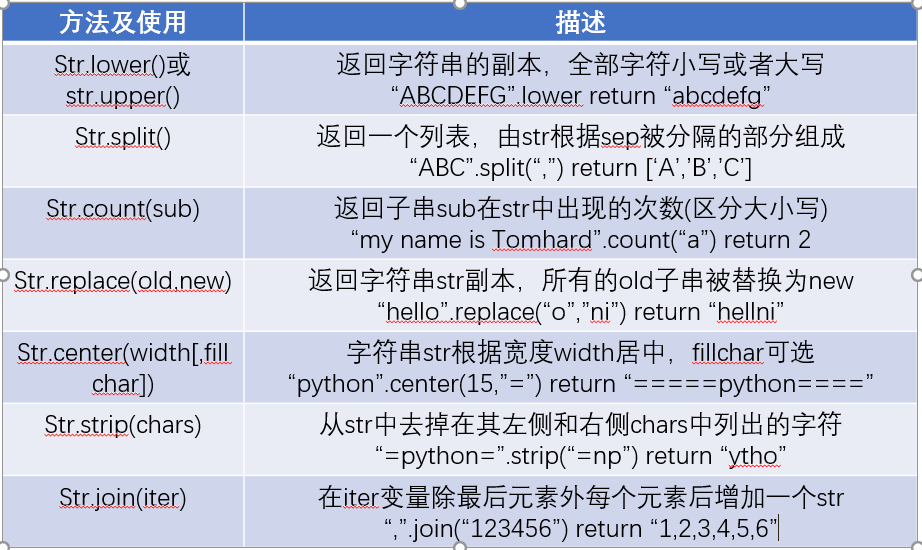
#字符串類型的格式化

三、time庫的使用

#時間獲取

*time():獲取計算機內部時間值，浮點數

-案例：time.time()

*ctime():獲取當前時間并以易讀的方式顯示出來，返回字符串

-案例：time.ctime()

*gmtime():獲取當前時間，表示為計算機可以處理的時間格式

-案例：time.gmtime()

#時間格式化:將時間以合理的方式顯示出來

*strftime(tpl,ts):tpl是格式化模板字符串，用來定義輸出效果；ts是計算機內部時間類型變量

-案例：>>>t=time.gmtime() >>>time.strftime("%Y-%m-%d %H:%M:%S",t)

*strptime(str,tpl)

str是字符串形式的時間值，tpl是格式化模板字符串，用來定義輸入效果。

>>>timeStr='2018-01-26 12:55:20'

>>>time.strptime(timeStr,"%Y-%m-%d %H:%M:%S")

#程序計時

*產生時間：sleep(s)

s擬休眠時間，單位是秒，可以是浮點數

>>>def wait():

time.sleep(3.3)

>>>wait() #程序等待3.3秒后再退出

*測量時間：perf_counter()

>>>start=time.perf_counter()

>>>end=time.perf_counter()

>>>end-start

#以上素材均來自嵩天先生的python語言程序設計課程