邏輯回歸本質是分類問題，而且是二分類問題，不屬于回歸，但是為什么又叫回歸呢。我們可以這樣理解，邏輯回歸就是用回歸的辦法來做分類。它是在線性回歸的基礎上，通過Sigmoid函數進行了非線性轉換，從而具有更強的擬合能力

sigmoid 函數

https://blog.csdn.net/fenglepeng/article/details/104829873

Logistic回歸分類器

為了實現Logistic回歸分類器，我們可以在每個特征上都乘以一個回歸系數，然后把所有的結果值相加，將這個總和代入Sigmoid函數中，進而得到一個范圍在0~1之間的數值。任何大于0.5的數據被分入1類，小于0.5即被歸入0類。所以，Logistic回歸也可以被看成是一種概率估計。

$\begin{aligned}p&=h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \end{aligned}$

所以說，Logistic回歸分類器可以看成線性回歸與sigmoid的混合函數，是一個二分類的模型（這里是取的0和1，有的算法是+1和-1）

$\hat{y}=\left\{\begin{matrix} 0,P(\hat{y}=1)>p\\ 1,P(\hat{y}=0)>p \end{matrix}\right.$

在用于分類時，實際上是找一個閾值，大于閾值的屬于1類別，小于的屬于0類別。（閾值是可根據具體情況進行相應變動的）

Logistic回歸及似然函數

我們假設

$\begin{aligned}P(y=1|x;\theta)&=h_\theta(x) \\P(y=0|x;\theta)&=1-h_\theta(x) \end{aligned}$

把兩個式子結合起來

$\begin{aligned}P(y|x;\theta)&=(h_\theta(x))^y(1-h_\theta(x))^{(1-y)}\end{aligned}$

運用極大似然估計得到似然函數

$\begin{aligned}L(\theta)&=p(\vec{y}|X;\theta) \\&=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta) \\&=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{(1-y^{(i)})}\end{aligned}$

累乘不好求，我們可以求其對數似然函數。最值的問題，求導（第三行到第四行使用了sigmoid函數求導）

$\begin{aligned}l(\theta)&=\log L(\theta) \\&=\sum_{i=1}^m(y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))) \\\frac{\partial l(\theta)}{\partial\theta_j}&=\sum_{i=1}^m(\frac{y^{(i)}}{h_\theta(x^{(i)})}-\frac{1-y^{(i)}}{1-h_\theta(x^{(i)})})\cdot\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j} \\&=\sum_{i=1}^m(\frac{y^{(i)}}{g(\theta^Tx^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^Tx^{(i)})})\cdot\frac{\partial g(\theta^Tx^{(i)})}{\partial\theta_j} \\&=\sum_{i=1}^m(\frac{y^{(i)}}{g(\theta^Tx^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^Tx^{(i)})})\cdot g(\theta^Tx^{(i)})(1-g(\theta^Tx^{(i)}))\cdot\frac{\partial\theta^Tx^{(i)}}{\partial\theta_j} \\&=\sum_{i=1}^m(y^{(i)}(1-g(\theta^Tx^{(i)}))-(1-y^{(i)})g(\theta^Tx^{(i)}))\cdot x_j^{(i)} \\&=\sum_{i=1}^m(y^{(i)}-g(\theta^Tx^{(i)}))\cdot x_j^{(i)}\end{aligned}$

求解，使用批量梯度下降法BGD

$\theta_j=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$

或者隨機梯度下降法SGD

$\theta_j=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$

可以發現邏輯回歸與線性回歸梯度下降求解的形式類似，唯一的區別在于假設函數hθ(x)不同，線性回歸假設函數為θTx，邏輯回歸假設函數為Sigmoid函數。

線性回歸模型服從正態分布，邏輯回歸模型服從二項分布（Bernoulli分布），因此邏輯回歸不能應用最小二乘法作為目標/損失函數，所以用梯度下降法。

極大似然估計與Logistic回歸損失函數

我們要讓對數似然函數最大，也就是他的相反數 $-l(\theta )$ 最小。而 $-l(\theta )$ 最小化，則可以看成損失函數，求其最小化：

$loss = -l(\theta )$

似然函數：

$\begin{aligned}L(\theta)&=\prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta) =\prod_{i=1}^mp_i^{y^{(i)}}(1-p_i)^{1-y^{(i)}} \end{aligned}$

logistic函數

$\begin{aligned}p_i&=h_\theta(x^{(i)}) =\frac{1}{1+e^{-\theta^Tx^{(i)}}} \end{aligned}$

帶入得

$\begin{aligned}\\l(\theta)&=\ln L(\theta) \\&=\sum_{i=1}^m\ln[p_i^{y^{(i)}}(1-p_i)^{1-y^{(i)}}] \\&=\sum_{i=1}^m\ln[(\frac{1}{1+e^{-f_i}})^{y^{(i)}}(\frac{1}{1+e^{f_i}})^{1-y^{(i)}}] \\loss(y^{(i)},\hat{y^{(i)}})&=-l(\theta) \\&=\sum_{i=1}^m[y^{(i)}\ln(1+e^{-f_i})+(1-y^{(i)})\ln(1+e^{f_i})] \\&=\begin{cases}\sum_{i=1}^m\ln(1+e^{-f_i}), &y^{(i)}=1 \\ \sum_{i=1}^m\ln(1+e^{f_i}), &y^{(i)}=0\end{cases} \\\Rightarrow loss(y^{(i)},\hat{y^{(i)}})&=\sum_{i=1}^m\ln(1+e^{(1-2y^{(i)})\theta^Tx^{(i)}}), y^{(i)}=\begin{cases}1 \\ 0\end{cases}\end{aligned}$

這個結果就是交叉熵損失函數。

總結

就一句話：通過以上過程，會發現邏輯回歸的求解，跟線性回歸的求解基本相同。

多分類問題（Multi-class classification）

????????對于分類多于2個的問題，可以將其看做二分類問題，即以其中一個分類作為一類，剩下的其他分類作為另一類，多分類問題的假設函數為?

$h_{0}^{i}(x)=p(y=i|x;\theta)$

one-vs-all/rest 問題解決方法：

訓練一個邏輯回歸分類器，預測 i 類別 y=i 的概率；
對一個新的輸入值x，為了作出類別預測，分別在k個分類器運行輸入值，選擇h最大的類別?

Softmax回歸模型??

Softmax回歸是logistic回歸的一般化模型，適用于k（k>2）分類的問題，第k類的參數為向量 $\theta_k$ ，組成的二維矩陣為 $\theta _{k*n}$ (k為類別數，n為特征數，即為每一個類別構建一個 $\theta_k$ ，用到的是ova思想)。

參考鏈接：機器學習之單標簽多分類及多標簽多分類

Softmax函數的本質就是將一個k維的任意實數向量映射成為另一個k維的實數向量，其中向量中的每個元素的取值都介于（0,1）之間。

Softmax回歸的概率函數為：

$p(y=k|x;\theta)=\frac{e^{\theta_k^Tx}}{\sum_{l=1}^{K}e^{\theta_l^{T}x}}, k=1,2,...,K$
注釋：? $e^{\theta_k^Tx}$ 計算的是，他屬于第k類的回歸值， $\sum_{l=1}^{K}e^{\theta_l^{T}x}$ 計算的是他屬于每個類別的累加，用e的指數是為了加大大的類別的影響

Softmax回歸的似然估計

似然函數：

$\begin{aligned}L(\theta)&=\prod_{i=1}^m\prod_{k=1}^Kp(y=k|x^{(i)};\theta)^{y_k^{(i)}} \\&=\prod_{i=1}^m\prod_{k=1}^K(\frac{e^{\theta_k^Tx}}{\sum_{l=1}^Ke^{\theta_l^Tx}})^{y_k^{(i)}}\end{aligned}$

對數似然函數：

$\begin{aligned}l(\theta)&=\ln L(\theta) \\&=\sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}(\theta_k^Tx^{(i)}-\ln\sum_{l=1}^Ke^{\theta_l^Tx^{(i)}}) \\l(\theta)&=\sum_{k=1}^Ky_k(\theta_k^Tx-\ln\sum_{l=1}^Ke^{\theta_l^Tx})\end{aligned}$

?推導和Logistic回歸類似，只是將分類的個數從2擴展到k的情形。Softmax算法的損失函數：

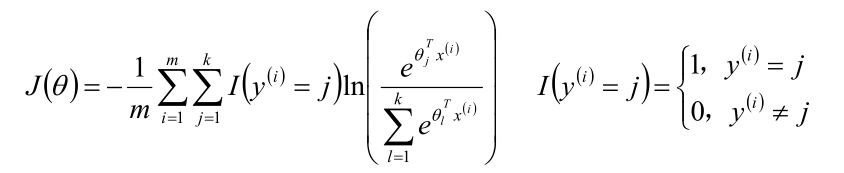
梯度下降法

總結

線性回歸模型一般用于回歸問題，邏輯回歸和Softmax回歸模型一般用于分類問題；
求θ的主要方式是梯度下降算法，該算法是參數優化的重要手段，主要使用SGD或MBGD；
邏輯回歸/Softmax回歸模型是實際問題中解決分類問題的最重要的方法；
廣義線性模型對樣本的要求不必一定要服從正態分布，只要服從指數分布簇（二項分布、Poisson分布、Bernoulli分布、指數分布等）即可；廣義線性模型的自變量可以是連續的也可以是離散的。
?