0. 相關概念

• 穩定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不穩定：如果a原本在b的前面，而a=b，排序之后 a 可能會出現在 b 的后面。
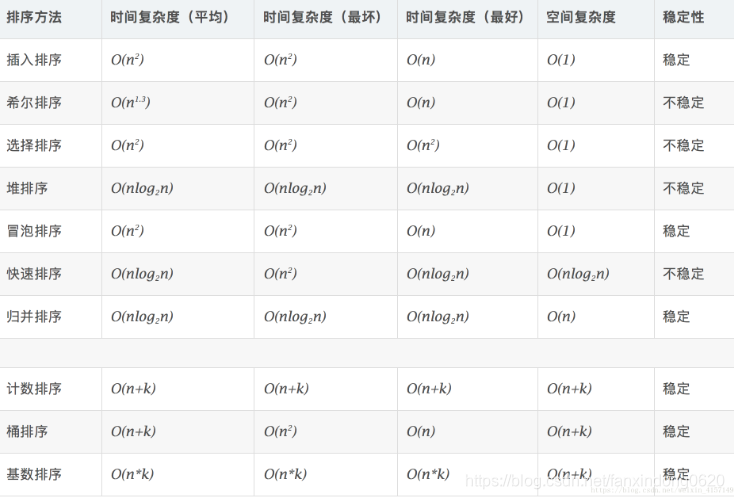
• 時間復雜度：對排序數據的總的操作次數。反映當n變化時，操作次數呈現什么規律。
• 空間復雜度：是指算法在計算機內執行時所需存儲空間的度量，它也是數據規模n的函數。
  

一. 冒泡排序

算法過程：
進行N-1趟操作，每一趟，都是不斷的比較相鄰的元素，那么一趟下來，就會將最大的移到排好順序的最后面的位置。

代碼實現：

def bubble_sort(alist):"""冒泡排序：最優時間復雜度：O（n）最壞時間復雜度：O（n^2）穩定性：穩定"""n = len(alist)for j in range(n-1):for i in range(0,n-1-j):if alist[i] > alist[i+1]:alist[i],alist[i+1] = alist[i+1],alist[i]return liif __name__ == '__main__':li = [54,26,93,17,77,31,44,55,20]print(li)li = bubble_sort(li)print(li)

二. 選擇排序

算法過程：
初始狀態：無序區為R[1…n]，有序區為空；

第i趟排序(i=1,2,3…n-1)開始時，當前有序區和無序區分別為R[1…i-1]和R(i…n）。該趟排序從當前無序區中-選出關鍵字最小的記錄 R[k]，將它與無序區的第1個記錄R交換，使R[1…i]和R[i+1…n)分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區；

n-1趟結束，數組有序化結束。

代碼實現：

def select_sort(alist):"""選擇排序最優時間復雜度：O（n^2）最壞時間復雜度：O（n^2）穩定性：不穩定"""n = len(alist)for j in range(n-1):min_index = jfor i in range(j+1,n):if alist[min_index] > alist[i]:min_index = ialist[j],alist[min_index] = alist[min_index],alist[j]if __name__ == '__main__':li = [54,26,93,17,77,26,31,44,55,20]print(li)select_sort(li)print(li)

三. 插入排序

算法過程：
從第一個元素開始，該元素可以認為已經被排序；

取出下一個元素，在已經排序的元素序列中從后向前掃描；

如果該元素（已排序）大于新元素，將該元素移到下一位置；

重復步驟3，直到找到已排序的元素小于或者等于新元素的位置；

將新元素插入到該位置后；

重復步驟2~5。

代碼實現：

def insert_sort(alist):"""插入排序：最優時間復雜度:O(n)最差時間復雜度：O(n^2)穩定性：穩定"""n = len(alist)for j in range(1, n):i = jwhile i > 0:if alist[i] < alist[i-1]:alist[i], alist[i-1] = alist[i-1], alist[i]i -= 1else:breakif __name__ == '__main__':li = [54,26,93,17,77,31,44,55,20]print(li)insert_sort(li)print(li)

四. 希爾排序

算法過程：
選擇一個增量序列t1，t2，…，tk，其中ti>tj，tk=1；

按增量序列個數k，對序列進行k 趟排序；

每趟排序，根據對應的增量ti，將待排序列分割成若干長度為m 的子序列，分別對各子表進行直接插入排序。僅增量因子為1 時，整個序列作為一個表來處理，表長度即為整個序列的長度。

代碼實現：

def shell_sort(alist):"""shell排序：最優時間度：根據步長序列的不同而不同最差時間度：O(n^2)穩定性：不穩定"""n = len(alist)gap = n // 2while gap > 0:# 希爾排序與插入排序的區別就是gap步長for j in range(gap,n):i = jwhile i > 0:if alist[i] < alist[i - gap]:alist[i], alist[i-gap] = alist[i-gap], alist[i]i -= gapelse:break# 縮短gap步長gap //= 2if __name__ == '__main__':li = [54,26,93,17,77,26,31,44,55,20]print(li)shell_sort(li)print(li)

五. 快速排序

算法過程：
從數列中挑出一個元素，稱為 “基準”（pivot）；

重新排序數列，所有元素比基準值小的擺放在基準前面，所有元素比基準值大的擺在基準的后面（相同的數可以到任一邊）。在這個分區退出之后，該基準就處于數列的中間位置。這個稱為分區（partition）操作；

遞歸地（recursive）把小于基準值元素的子數列和大于基準值元素的子數列排序。

代碼實現：

def quick_sort(alist,first,last):"""快速排序：最優復雜度：O（nlogn）最壞復雜度：O（n^2）穩定性:不穩定"""if first >= last:returnmid_value = alist[first]low = firsthigh = lastwhile low < high:while low < high and alist[high] >= mid_value:high -= 1alist[low] = alist[high]while low < high and alist[low] < mid_value:low += 1alist[high] = alist[low]# 從循環退出時，low=highalist[low] = mid_value# 對low左邊的列表執行快速排序quick_sort(alist,first,low-1)# 對low右邊的列表排序quick_sort(alist,low+1,last)if __name__ == '__main__':li = [54, 26, 93, 17, 77, 31, 44, 55, 20]print(li)quick_sort(li, 0, len(li)-1)print(li)

六. 歸并排序

算法過程：

把長度為n的輸入序列分成兩個長度為n/2的子序列；

對這兩個子序列分別采用歸并排序；

將兩個排序好的子序列合并成一個最終的排序序列。

代碼實現：

def merge_sort(alist):"""歸并排序最優時間度：最壞時間度：穩定性："""n = len(alist)if n <= 1:return alistmid = n//2# left采用歸并排序后形成的有序的新的列表left_li = merge_sort(alist[:mid])# right采用歸并排序后形成的有序的新的列表right_li = merge_sort(alist[mid:])# 將兩個有序的子序列合并為一個新的整體left_pointer,right_pointer = 0,0result = []while left_pointer<len(left_li) and right_pointer<len(right_li):if left_li[left_pointer] < right_li[right_pointer]:result.append(left_li[left_pointer])left_pointer += 1else:result.append(right_li[right_pointer])right_pointer += 1result += left_li[left_pointer:]result += right_li[right_pointer:]return resultif __name__ == '__main__':li = [54,26,93,17,77,31,44,55,20]print(li)li_sort = merge_sort(li)print(li_sort)

七. 其他

其他算法的詳細過程請參考：https://blog.csdn.net/weixin_41571493/article/details/81875088