樹鏈剖分入門

這幾天學了一個樹鏈剖分，覺得還不是很難，這里我試著講一講吧。

首先，我認為樹鏈剖分是把在樹上一個節點一個節點的走改為按照某種規則跳，從而降低了時間復雜度。

那這是什么規則呢？

首先我們得知道什么是重鏈，知道什么是重鏈就得先知道什么是重兒子，重兒子就是子樹較大的兒子。然后對于一個點，我們總是往他的重兒子走，這樣就構成了重鏈，那么剩下的就是輕鏈。

放張圖直觀些

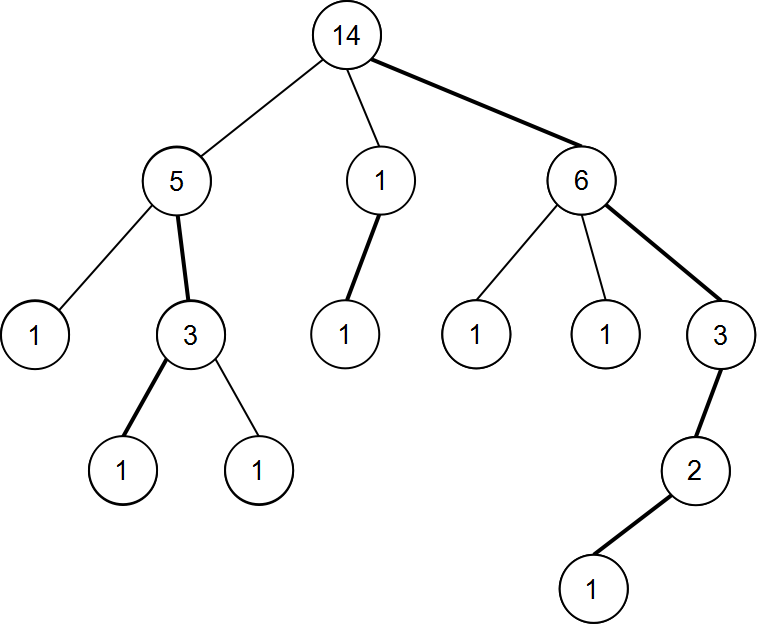
然后我們同樣可以對樹進行dfs，只不過重兒子優先，這樣我們也得到了一個dfs序，于是我們把樹上問題成功轉化成了線性問題。接著就可以用線段樹等數據結構維護了。

那就拿這道板子體為例：https://www.luogu.org/problemnew/show/P3384

首先是兩遍dfs，第一遍dfs維護子樹大小size[]，節點深度dep[]，重兒子son[]，以及一個節點的父親節點（因為如果跳到了一條鏈的頂端，就要再自己走到他的父親節點）。

 1 void dfs1(int now)
 2 {
 3     vis[now] = 1;
 4     size[now] = 1;
 5     for(int i = 0; i < (int)v[now].size(); ++i)
 6     {
 7         if(!vis[v[now][i]])
 8         {
 9             dep[v[now][i]] = dep[now] + 1;
10             fa[v[now][i]] = now;
11             dfs1(v[now][i]);
12             size[now] += size[v[now][i]];
13             if(!son[now] || size[son[now]] < size[v[now][i]]) son[now] = v[now][i];
14             //如果沒有重兒子，或者當前子樹大小大于重兒子的子樹大小，就更新重兒子 
15         }
16     }
17 }

第二遍dfs是維護dfs序dfsx[]，每一條鏈的頂端是哪一個節點。但我們還要在維護一個pos[]，因為當我們將樹轉化成線性后，用線段樹建樹的時候需要添加節點，而這個節點的編號是dfs序的編號，所以需要再用一個數組記錄dfs序的編號所對應的樹上節點編號。

 1 int cnt = 0, dfsx[maxn], pos[maxn], top[maxn];
 2 void dfs2(int now)
 3 {
 4     //dfsx[]因為智慧更新一次，所以可以當做vis[]用 
 5     dfsx[now] = ++cnt; pos[cnt] = now;
 6     if(son[now])
 7     {
 8         top[son[now]] = top[now];
 9         dfs2(son[now]);        //優先走重兒子，保證一條鏈在dfs序上的編號是連續的 
10     }
11     for(int i = 0; i < (int)v[now].size(); ++i)
12     {
13         if(!dfsx[v[now][i]] && son[now] != v[now][i])    //再走不是重兒子的節點 
14         {
15             top[v[now][i]] = v[now][i];        //輕兒子所在的鏈只有他自己一個節點，所以頂端節點就是他自己 
16             dfs2(v[now][i]);
17         }
18     }
19 }

這兩個預處理完事后就可以看看題了。

第一個詢問，將樹從x到y結點最短路徑上所有節點的值都加上z。

首先我們要將x，y移到同一條鏈上，具體操作就是如果其中一個點所在鏈的頂端的深度更低，就將他跳到鏈的頂端，并更新他到頂端節點的區間。

移到同一條鏈上后，就更新這兩個點的區間就行了

 1 void pathUpdate(int x, int y, int z)
 2 {
 3     while(top[x] != top[y])        //先把這倆搞到一條鏈上 
 4     {
 5         if(dep[top[x]] < dep[top[y]]) swap(x, y);    //默認讓x跳 
 6         update(dfsx[top[x]], dfsx[x], 1, z);
 7         x = fa[top[x]];
 8     }
 9     if(dfsx[x] > dfsx[y]) swap(x, y);
10     update(dfsx[x], dfsx[y], 1, z);
11 }

操作2：求樹從x到y結點最短路徑上所有節點的值之和

和修改一樣，先把兩點移到同一條鏈上，然后計算跳的點在該鏈上的貢獻

 1 ll pathQuery(int x, int y)
 2 {
 3     ll ret = 0;
 4     while(top[x] != top[y])
 5     {
 6         if(dep[top[x]] < dep[top[y]]) swap(x, y);
 7         ret += query(dfsx[top[x]], dfsx[x], 1); ret %= mod;
 8         x = fa[top[x]];
 9     }
10     if(dfsx[x] > dfsx[y]) swap(x, y);
11     ret += query(dfsx[x], dfsx[y], 1); ret %= mod;
12     return ret;
13 }

操作3：將以x為根節點的子樹內所有節點值都加上z

值得一提的是，盡管我們在維護dfs序時是重鏈優先遍歷，但仍滿足一個節點以及他的子樹在dfs序上是一段長為子樹大小的連續區間，自己畫一畫就明白了

這里和查詢放一塊

1 void sbtUpdate(int x, int z)
2 {
3     update(dfsx[x], dfsx[x] + size[x] - 1, 1, z);
4 }
5 ll sbtQuery(int x)
6 {
7     return query(dfsx[x], dfsx[x] + size[x] - 1, 1);
8 }

這樣板子就寫完了，是不是很簡單？

然后最重要的一件事是別忘了取模，而且每一個運算后都要取，否則你就可能70分代碼debug一小時……

  1 #include<cstdio>
  2 #include<iostream>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<algorithm>
  6 #include<vector>
  7 #include<cctype>
  8 using namespace std;
  9 #define enter printf("\n")
 10 #define space printf(" ")
 11 typedef long long ll;
 12 const int INF = 0x3f3f3f3f;
 13 const int maxn = 1e5 + 5;
 14 inline ll read()
 15 {
 16     ll ans = 0;
 17     char ch = getchar(), last = ' ';
 18     while(!isdigit(ch)) {last = ch; ch = getchar();}
 19     while(isdigit(ch))
 20     {
 21         ans = ans * 10 + ch - '0'; ch = getchar();    
 22     }
 23     if(last == '-') ans = -ans;
 24     return ans;
 25 }
 26 inline void write(ll x)
 27 {
 28     if(x < 0) x = -x, putchar('-');
 29     if(x >= 10) write(x / 10);
 30     putchar('0' + x % 10);
 31 }
 32 
 33 int n, m, s, mod;
 34 int a[maxn];
 35 vector<int> v[maxn];
 36 
 37 bool vis[maxn];
 38 int fa[maxn], son[maxn], size[maxn], dep[maxn];
 39 void dfs1(int now)
 40 {
 41     vis[now] = 1;
 42     size[now] = 1;
 43     for(int i = 0; i < (int)v[now].size(); ++i)
 44     {
 45         if(!vis[v[now][i]])
 46         {
 47             dep[v[now][i]] = dep[now] + 1;
 48             fa[v[now][i]] = now;
 49             dfs1(v[now][i]);
 50             size[now] += size[v[now][i]];
 51             if(!son[now] || size[son[now]] < size[v[now][i]]) son[now] = v[now][i];
 52             //如果沒有重兒子，或者當前子樹大小大于重兒子的子樹大小，就更新重兒子 
 53         }
 54     }
 55 }
 56 //第二遍dfs是維護dfs序dfsx[]，每一條鏈的頂端是哪一個節點
 57 
 58 int cnt = 0, dfsx[maxn], pos[maxn], top[maxn];
 59 void dfs2(int now)
 60 {
 61     //dfsx[]因為智慧更新一次，所以可以當做vis[]用 
 62     dfsx[now] = ++cnt; pos[cnt] = now;
 63     if(son[now])
 64     {
 65         top[son[now]] = top[now];
 66         dfs2(son[now]);        //優先走重兒子，保證一條鏈在dfs序上的編號是連續的 
 67     }
 68     for(int i = 0; i < (int)v[now].size(); ++i)
 69     {
 70         if(!dfsx[v[now][i]] && son[now] != v[now][i])    //再走不是重兒子的節點 
 71         {
 72             top[v[now][i]] = v[now][i];        //輕兒子所在的鏈只有他自己一個節點，所以頂端節點就是他自己 
 73             dfs2(v[now][i]);
 74         }
 75     }
 76 }
 77 
 78 int l[maxn << 2], r[maxn << 2];
 79 ll sum[maxn << 2], lazy[maxn << 2];
 80 void build(int L, int R, int now)
 81 {
 82     l[now] = L; r[now] = R;
 83     if(L == R) {sum[now] = a[pos[L]]; return;}
 84     int mid = (L + R) >> 1;
 85     build(L, mid, now << 1);
 86     build(mid + 1, R, now << 1 | 1);
 87     sum[now] = (sum[now << 1] + sum[now << 1 | 1]) % mod; 
 88 }
 89 void pushdown(int now)
 90 {
 91     if(lazy[now])
 92     {
 93         lazy[now << 1] += lazy[now]; lazy[now << 1] %= mod;
 94         lazy[now << 1 | 1] += lazy[now]; lazy[now << 1 | 1] %= mod;
 95         sum[now << 1] += (ll)(r[now << 1] - l[now << 1] + 1) * lazy[now]; sum[now << 1] %= mod;
 96         sum[now << 1 | 1] += (ll)(r[now << 1 | 1] - l[now << 1 | 1] + 1) * lazy[now]; sum[now << 1 | 1] %= mod;
 97         lazy[now] = 0;
 98     }
 99 }
100 void update(int L, int R, int now, int d)
101 {
102     if(L == l[now] && R == r[now])
103     {
104         sum[now] += (ll)(r[now] - l[now] + 1) * d; sum[now] %= mod;
105         lazy[now] += d; lazy[now] %= mod;
106         return;
107     }
108     pushdown(now);
109     int mid = (l[now] + r[now]) >> 1;
110     if(R <= mid) update(L, R, now << 1, d);
111     else if(L > mid) update(L, R, now << 1 | 1, d);
112     else {update(L, mid, now << 1, d); update(mid + 1, R, now << 1 | 1, d);}
113     sum[now] = sum[now << 1] + sum[now << 1 | 1];
114 }
115 ll query(int L, int R, int now)
116 {
117     if(L == l[now] && R == r[now]) return sum[now];
118     pushdown(now);
119     int mid = (l[now] + r[now]) >> 1;
120     if(R <= mid) return query(L, R, now << 1);
121     else if(L > mid) return query(L, R, now << 1 | 1);
122     else return (query(L, mid, now << 1) + query(mid + 1, R, now << 1 | 1)) % mod;
123 }
124 
125 void pathUpdate(int x, int y, int z)
126 {
127     while(top[x] != top[y])        //先把這倆搞到一條鏈上 
128     {
129         if(dep[top[x]] < dep[top[y]]) swap(x, y);    //默認讓x跳 
130         update(dfsx[top[x]], dfsx[x], 1, z);
131         x = fa[top[x]];
132     }
133     if(dfsx[x] > dfsx[y]) swap(x, y);
134     update(dfsx[x], dfsx[y], 1, z);
135 }
136 ll pathQuery(int x, int y)
137 {
138     ll ret = 0;
139     while(top[x] != top[y])
140     {
141         if(dep[top[x]] < dep[top[y]]) swap(x, y);
142         ret += query(dfsx[top[x]], dfsx[x], 1); ret %= mod;
143         x = fa[top[x]];
144     }
145     if(dfsx[x] > dfsx[y]) swap(x, y);
146     ret += query(dfsx[x], dfsx[y], 1); ret %= mod;
147     return ret;
148 }
149 
150 void sbtUpdate(int x, int z)
151 {
152     update(dfsx[x], dfsx[x] + size[x] - 1, 1, z);
153 }
154 ll sbtQuery(int x)
155 {
156     return query(dfsx[x], dfsx[x] + size[x] - 1, 1);
157 }
158 
159 int main()
160 {
161     n = read(); m = read(); s = read(); mod = read();
162     for(int i = 1; i <= n; ++i) a[i] = read();
163     for(int i = 1 ; i < n; ++i)
164     {
165         int a = read(), b = read();
166         v[a].push_back(b); v[b].push_back(a);
167     }
168     dfs1(s); 
169     top[s] = s; dfs2(s);    
170     build(1, n, 1);
171     for(int i = 1; i <= m ; ++i)
172     {
173         int d = read();
174         if(d == 1) 
175         {
176             int x = read(), y = read(), z = read();
177             pathUpdate(x, y, z);
178         }
179         else if(d == 2)
180         {
181             int x = read(), y = read();
182             write(pathQuery(x, y)); enter;
183         }
184         else if(d == 3)
185         {
186             int x = read(), z = read();
187             sbtUpdate(x, z);
188         }
189         else
190         {
191             int x = read();
192             write(sbtQuery(x)); enter;
193         }
194     }
195     return 0;
196 }