19_05_01校內訓練[polygon]

題意

把一個邊長為1的正n邊形放到一個正m邊形中，要求m邊形完全覆蓋n邊形，可以有交點，并且中心重合。求正m邊形的最小邊長，至少精確到6位。要求logn計算。

思考

先考慮m|n的情況。

我們知道，正m邊形的邊長與可行區域（即可以完全覆蓋的那些角度）形成單射，當且僅當所有可行區域都成為可數的點時，答案最優。（可以理解為再縮小一點就無解了）

這樣不難證明，把正n邊形的幾條邊剛好卡在正m邊形上是最優的。如n=8，m=4：

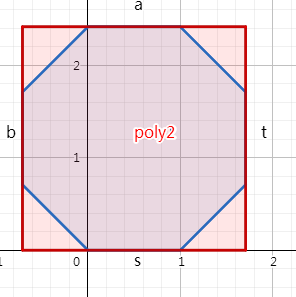
這時正m邊形的邊長是容易計算的。相信大家都會初中數學。

這樣再考慮一般情況。由于是中心重合，正n邊形旋轉2π/m度后仍然是能被覆蓋的。

在所有可行的旋轉過程中，將最外圈的點連起來，仍然形成一個正多邊形，且邊數為lcm(n,m)。

例如，n=4，m=6：

用紫線圍出來的正12邊形即為正方形得到的結果。

至于正確性，在于所有的可行區域都是單點。

這樣一來，就可以直接轉化為上一個問題。公式認真推即可。

代碼

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long int ll;
 4 const double pi=acos(-1);
 5 ll n,m;
 6 ll gcd(ll x,ll y)
 7 {
 8     return x%y==0?y:gcd(y,x%y);
 9 }
10 ll lcm(ll x,ll y)
11 {
12     return x/gcd(x,y)*y;
13 }
14 double solve(ll n,ll m)
15 {
16     double len=1/(2*tan(pi/n));
17     double th=(n/m)*pi/n;
18     return tan(th)*len*2;
19 }
20 int main()
21 {
22     ios::sync_with_stdio(false);
23     cin>>n>>m;
24     double len=1/(2*sin(pi/n));
25     n=lcm(n,m);
26     double a=sin(pi/n)*len*2;
27     cout<<fixed<<setprecision(9)<<solve(n,m)*a<<endl;
28     return 0;
29 }

View Code

轉載于:https://www.cnblogs.com/GreenDuck/p/10799543.html

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/449081.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/449081.shtml
英文地址，請注明出處：http://en.pswp.cn/news/449081.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！