數據結構7.3_圖的遍歷

我們希望從圖中某一頂點出發訪遍圖中其余頂點，且使每一個頂點僅被訪問一次。

這一過程就叫做圖的遍歷。

圖的遍歷算法是求解圖的連通性問題、拓撲排序和求關鍵路徑等算法的基礎。

然而，圖的遍歷要比樹的遍歷復雜得多。

因為圖的任一頂點都可能和其余的頂點相鄰接。

所以，在訪問了某個頂點之后，可能沿著某條路徑搜索之后，又回到該頂點上。

為了避免同一頂點被訪問多次，在遍歷圖的過程中，必須記下每個已訪問過的頂點。

為此，我們可以設一個輔助數組visited[0...n-1]，它的初始值置為“假”或者零，一旦訪問了頂點vi，便置visted[i]為“真”或者為被訪問時的次序號。

通常有兩條遍歷圖的路徑：深度優先搜索和廣度優先搜索。

它們對于無向圖和有向圖都適用。

===================================================

深度優先搜索

（Depth First Search） DFS

這種遍歷類似于樹的先根遍歷，是樹的先根遍歷的一種推廣。

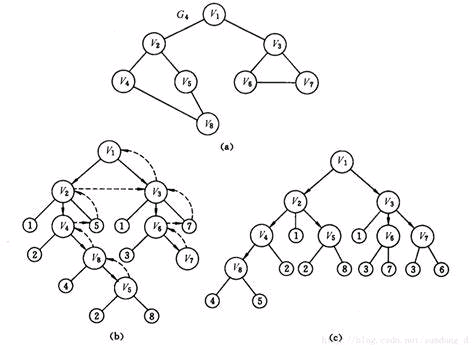
圖（a）是一張無向圖

圖（b）是深度優先搜索的過程

圖（c）是廣度優先搜索的過程

假設初始狀態是圖中所有頂點未曾被訪問，則深度優先搜索可從圖中某個頂點v出發，訪問此頂點，然后依次從v的未被訪問的鄰接點出發深度優先遍歷圖，直至圖中所有和v有路徑相通的頂點都被訪問到；

若此圖中尚有頂點未被訪問，則另選圖中一個未曾被訪問的頂點作為起點，重復上述過程，直至圖中所有頂點都被訪問為止。

為了在遍歷過程中便于區分頂點是否已被訪問，許附設訪問標志數組visited[0 ... n-1]，其初值為“false”，一旦某個頂點被訪問，則其相應的分量置為“true”。

 1 Boolean visited[MAX];
 2 Status (*VisitFunc)(int v);
 3 
 4 void DFSTraverse(Graph G, Status(* Visit)(int v)) { //對圖G作深度優先遍歷
 5     VisitFunc = Visit;  //使用全局變量VisitFunc,使DFS不必設函數指針參數
 6     for(v=0; v<G.vexnum; ++v)  visited[v] = FALSE;  //訪問標志數組初始化
 7     for(v=0; v<G.vexnum; ++v)
 8         if(!visited[w])  DFS(G, w);  //對尚未訪問的頂點調用DFS
 9 
10 }
11 
12 
13 void DFS(Graph G, int v) {
14     //從第v個頂點出發遞歸地深度優先遍歷圖G
15     visited[v] = TRUE;
16     VisitFunc(v);  //訪問第v個頂點
17     for(w = FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w))
18         if(!visited[w])  DFS(G, w);  //對尚未訪問的鄰接頂點w，遞歸調用DFS
19 
20 }

遍歷的過程實際上是對每個頂點查找其鄰接點的過程。其耗費的時間取決于所采用的存儲結構。

當使用二維數組表示鄰接矩陣作為圖的存儲結構時，查找每個頂點的鄰接點所需時間為O(n^2)，其中n為圖中頂點數。

當以鄰接表作為圖的存儲結構時，找鄰接點所需時間為O(e)，其中e為無向圖中的邊的書或有向圖中弧的數。

因此當以鄰接表作為存儲結構時，深度優先搜索遍歷圖的時間復雜度為O(n+e)。

===================================================

廣度優先搜索

（Breadth First Search） BFS?

廣度優先搜索遍歷類似于樹的按層次遍歷的過程。

假設從圖中的某頂點v出發，在訪問了v之后依次訪問v的各個未曾訪問過的鄰接點，

然后分別從這些鄰接點出發依次訪問它們的鄰接點，并使“先被訪問的頂點的鄰接點”先于“后被訪問的頂點的鄰接點”被訪問，

直到圖中所有已被訪問的頂點的鄰接點都被訪問到。

若此時圖中尚有頂點未被訪問，則另選圖中一個未曾被訪問的頂點作為起始點，重復上述過程，

直至圖中所有頂點都被訪問到為止。

換句話說，廣度優先搜索遍歷圖的過程是以v為起始點，由近至遠，依次訪問v有路徑相通且路徑長度為1,2，...的頂點。

例如對圖a進行廣度優先搜索遍歷圖如圖c所示。

和深度優先搜索類似，在遍歷的過程中也需要一個訪問標志數組。

并且，為了順次訪問路徑長度為2、3、...的頂點，需附設隊列以存儲已被訪問的路徑長度為1,2，...的頂點。

 1 void BFSTraverse(Graph G, Status(*Visit)(int v)) {
 2     //按廣度優先非遞歸遍歷圖G。使用輔助隊列Q和訪問標志數組visited
 3     for(v = 0; v<G.vexnum; ++v)
 4         visited[v] = FALSE;
 5     InitQueue(Q);  //置空輔助隊列Q
 6     for(v = 0; v<G.vexnum; ++v)
 7     {
 8         if(!visited[v])
 9         {
10             visited[v] = TRUE;
11             Visit(v);
12             EnQueu(Q, v)  //v入隊列
13             while(!QueueEmpyt(Q)) {
14                 DeQueue(Q,u);      //隊頭元素出隊并置為u
15                 for(w= FirstAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w))
16                     if(!Visited[w]) { //w為u的尚未訪問的鄰接頂點
17                         Visited[w] = TRUE;
18                         Visite(w);
19                         EnQueue(Q,W);
20                     } 
21         }
22     }
23 
24 }

分析上述算法，每個頂點至多進一次隊列。

遍歷圖的過程實質上通過邊或弧找鄰接點的過程。

因此廣度優先搜索遍歷圖的時間復雜度和深度優先搜索遍歷相同，兩者不同之處僅僅在于對頂點訪問的順序不同。

轉載于:https://www.cnblogs.com/grooovvve/p/10828044.html

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/448865.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/448865.shtml
英文地址，請注明出處：http://en.pswp.cn/news/448865.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！