一、概述
? ? ? ?排序有內部排序和外部排序,內部排序是數據記錄在內存中進行排序,而外部排序是因排序的數據很大,一次不能容納全部的排序記錄,在排序過程中需要訪問外存。
? ? ? ?我們這里說說八大排序就是內部排序。
? ? ? ?當n較大,則應采用時間復雜度為O(nlog2n)的排序方法:快速排序、堆排序或歸并排序序。
? ? ? ?快速排序:是目前基于比較的內部排序中被認為是最好的方法,當待排序的關鍵字是隨機分布時,快速排序的平均時間最短。
? ? ? ?下面我們來分別介紹這8中排序算法。
二、排序算法
1、插入排序——直接插入排序
使用場景:
? ? ? ?經常碰到這樣一類排序問題:把新的數據插入到已經排好的數據列中。
基本思想:
? ? ? ?1)將第一個數和第二個數排序,然后構成一個有序序列;
? ? ? ?2)將第三個數插入進去,構成一個新的有序序列;
? ? ? ?3)對第四個數、第五個數……直到最后一個數,重復第二步。
實現邏輯:
? ? ? ?1)首先設定插入次數,即循環次數,for(int i=1;i<length;i++),1個數的那次不用插入;
? ? ? ?2)設定插入數和得到已經排好序列的最后一個數的位數。insertNum和j=i-1;
? ? ? ?3)從最后一個數開始向前循環,如果插入數小于當前數,就將當前數向后移動一位;
? ? ? ?4)將當前數放置到空著的位置,即j+1。
代碼示例:
public void insertSort(int[] a){int length=a.length;//數組長度,將這個提取出來是為了提高速度。int insertNum;//要插入的數for(int i=1;i<length;i++){//插入的次數insertNum=a[i];//要插入的數int j=i-1;//已經排序好的序列元素個數while(j>=0&&a[j]>insertNum){//序列從后到前循環,將大于insertNum的數向后移動一格a[j+1]=a[j];//元素移動一格j--;}a[j+1]=insertNum;//將需要插入的數放在要插入的位置。}}
2、插入排序——希爾排序
使用場景:
? ? ? ?對于直接插入排序問題,數據量巨大時。
基本思想:
? ? ? ?1)將數的個數設為n,取奇數k=n/2,將下標差值為k的書分為一組,構成有序序列;
? ? ? ?2)再取k=k/2 ,將下標差值為k的書分為一組,構成有序序列;
? ? ? ?3)重復第二步,直到k=1執行簡單插入排序。
實現邏輯:
? ? ? ?1)首先確定分的組數。
? ? ? ?2)然后對組中元素進行插入排序。
? ? ? ?3)然后將length/2,重復1,2步,直到length=0為止。
代碼示例:
public void sheelSort(int[] a){int d = a.length;while (d!=0) {d=d/2;for (int x = 0; x < d; x++) {//分的組數for (int i = x + d; i < a.length; i += d) {//組中的元素,從第二個數開始int j = i - d;//j為有序序列最后一位的位數int temp = a[i];//要插入的元素for (; j >= 0 && temp < a[j]; j -= d) {//從后往前遍歷。a[j + d] = a[j];//向后移動d位}a[j + d] = temp;}}}}3、選擇排序——簡單選擇排序
使用場景:
? ? ? ?常用于取序列中最大最小的幾個數時。
基本思想:
? ? ? ?如果每次比較都交換,那么就是交換排序;如果每次比較完一個循環再交換,就是簡單選擇排序。
? ? ? ?1)在要排序的一組數中,選出最小(或者最大)的一個數與第1個位置的數交換;
? ? ? ?2)然后在剩下的數當中再找最小(或者最大)的與第2個位置的數交換;
? ? ? ?3)依次類推,直到第n-1個元素(倒數第二個數)和第n個元素(最后一個數)比較為止。
實現邏輯:
? ? ? ?1)首先確定循環次數,并且記住當前數字和當前位置;
? ? ? ?2)將當前位置后面所有的數與當前數字進行對比,小數賦值給key,并記住小數的位置;
? ? ? ?3)比對完成后,將最小的值與第一個數的值交換;
? ? ? ?4)重復2、3步。
代碼示例:
public void selectSort(int[] a) {int length = a.length;for (int i = 0; i < length; i++) {//循環次數int key = a[i];int position=i;for (int j = i + 1; j < length; j++) {//選出最小的值和位置if (a[j] < key) {key = a[j];position = j;}}a[position]=a[i];//交換位置a[i]=key;}}簡單選擇排序的改進——二元選擇排序
? ? ? ?簡單選擇排序,每趟循環只能確定一個元素排序后的定位。我們可以考慮改進為每趟循環確定兩個元素(當前趟最大和最小記錄)的位置,從而減少排序所需的循環次數。改進后對n個數據進行排序,最多只需進行[n/2]趟循環即可。
代碼示例:
void SelectSort(int r[],int n) { int i ,j , min ,max, tmp; for (i=1 ;i <= n/2;i++) { // 做不超過n/2趟選擇排序 min = i; max = i ; //分別記錄最大和最小關鍵字記錄位置 for (j= i+1; j<= n-i; j++) { if (r[j] > r[max]) { max = j ; continue ; } if (r[j]< r[min]) { min = j ; } } //該交換操作還可分情況討論以提高效率 tmp = r[i-1]; r[i-1] = r[min]; r[min] = tmp; tmp = r[n-i]; r[n-i] = r[max]; r[max] = tmp; }
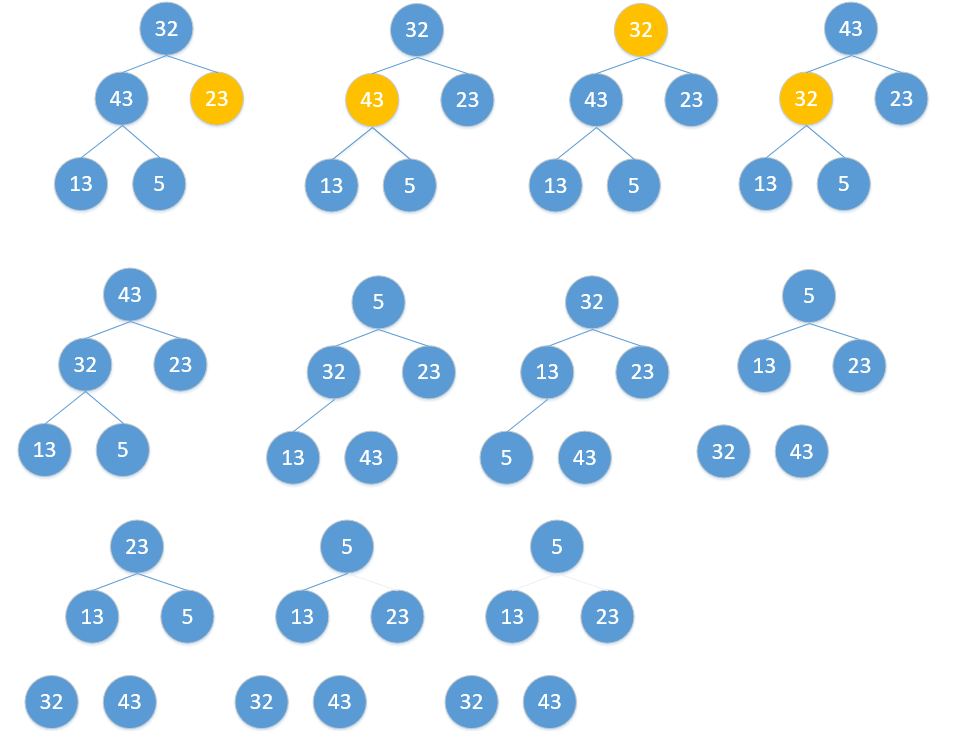
} 4、選擇排序——堆排序
? ? ? ?堆排序是一種樹形選擇排序,是對直接選擇排序的有效改進。
使用場景:
? ? ? ?對簡單選擇排序的優化。
基本思想:
? ? ? ?堆的定義如下:具有n個元素的序列(k1,k2,...,kn),當且僅當滿足
時稱之為堆。由堆的定義可以看出,堆頂元素(即第一個元素)必為最小項(小頂堆)。
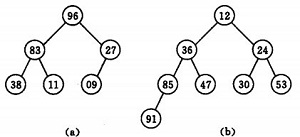
? ? ? ?若以一維數組存儲一個堆,則堆對應一棵完全二叉樹,且所有非葉結點的值均不大于(或不小于)其子女的值,根結點(堆頂元素)的值是最小(或最大)的。如:
? ? ? ?(a)大頂堆序列:(96, 83,27,38,11,09)
? ? ? ?(b)小頂堆序列:(12,36,24,85,47,30,53,91)
? ? ? ?初始時把要排序的n個數的序列看作是一棵順序存儲的二叉樹(一維數組存儲二叉樹),調整它們的存儲序,使之成為一個堆,將堆頂元素輸出,得到n 個元素中最小(或最大)的元素,這時堆的根節點的數最小(或者最大)。然后對前面(n-1)個元素重新調整使之成為堆,輸出堆頂元素,得到n 個元素中次小(或次大)的元素。依此類推,直到只有兩個節點的堆,并對它們作交換,最后得到有n個節點的有序序列。稱這個過程為堆排序。
? ? ? ?因此,實現堆排序需解決兩個問題:
? ? ? ?1、如何將n 個待排序的數建成堆;
? ? ? ?2、輸出堆頂元素后,怎樣調整剩余n-1 個元素,使其成為一個新堆。
首先討論第二個問題:輸出堆頂元素后,對剩余n-1元素重新建成堆的調整過程。
調整小頂堆的方法:
? ? ? ?1)設有m 個元素的堆,輸出堆頂元素后,剩下m-1 個元素。將堆底元素送入堆頂((最后一個元素與堆頂進行交換),堆被破壞,其原因僅是根結點不滿足堆的性質。
? ? ? ?2)將根結點與左、右子樹中較小元素的進行交換。
? ? ? ?3)若與左子樹交換:如果左子樹堆被破壞,即左子樹的根結點不滿足堆的性質,則重復方法 (2).
? ? ? ?4)若與右子樹交換,如果右子樹堆被破壞,即右子樹的根結點不滿足堆的性質。則重復方法 (2).
? ? ? ?5)繼續對不滿足堆性質的子樹進行上述交換操作,直到葉子結點,堆被建成。
稱這個自根結點到葉子結點的調整過程為篩選。如圖:
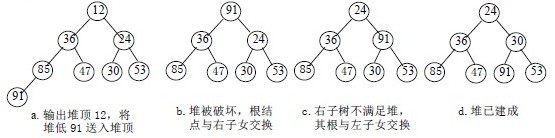
再討論對n 個元素初始建堆的過程。
建堆方法:對初始序列建堆的過程,就是一個反復進行篩選的過程。
? ? ? ?1)n 個結點的完全二叉樹,則最后一個結點是第 個結點的子樹。
個結點的子樹。
? ? ? ?2)篩選從第 個結點為根的子樹開始,該子樹成為堆。
個結點為根的子樹開始,該子樹成為堆。
? ? ? ?3)之后向前依次對各結點為根的子樹進行篩選,使之成為堆,直到根結點。
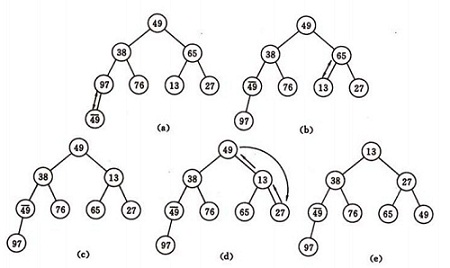
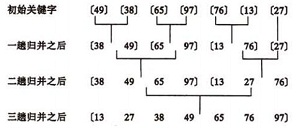
如圖建堆初始過程:無序序列:(49,38,65,97,76,13,27,49)
? ? ? ?1)將序列構建成大頂堆;
? ? ? ?2)將根節點與最后一個節點交換,然后斷開最后一個節點;
? ? ? ?3)重復第一、二步,直到所有節點斷開。
代碼示例:
public void heapSort(int[] a){System.out.println("開始排序");int arrayLength=a.length;//循環建堆 for(int i=0;i<arrayLength-1;i++){//建堆 buildMaxHeap(a,arrayLength-1-i);//交換堆頂和最后一個元素 swap(a,0,arrayLength-1-i);System.out.println(Arrays.toString(a));}}private void swap(int[] data, int i, int j) {// TODO Auto-generated method stub int tmp=data[i];data[i]=data[j];data[j]=tmp;}//對data數組從0到lastIndex建大頂堆 private void buildMaxHeap(int[] data, int lastIndex) {// TODO Auto-generated method stub //從lastIndex處節點(最后一個節點)的父節點開始 for(int i=(lastIndex-1)/2;i>=0;i--){//k保存正在判斷的節點 int k=i;//如果當前k節點的子節點存在 while(k*2+1<=lastIndex){//k節點的左子節點的索引 int biggerIndex=2*k+1;//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k節點的右子節點存在 if(biggerIndex<lastIndex){//若果右子節點的值較大 if(data[biggerIndex]<data[biggerIndex+1]){//biggerIndex總是記錄較大子節點的索引 biggerIndex++;}}//如果k節點的值小于其較大的子節點的值 if(data[k]<data[biggerIndex]){//交換他們 swap(data,k,biggerIndex);//將biggerIndex賦予k,開始while循環的下一次循環,重新保證k節點的值大于其左右子節點的值 k=biggerIndex;}else{break;}}}}
5、交換排序——冒泡排序
使用場景:
? ? ? ?一般不用。
基本思想:
? ? ? ?1)將序列中所有元素兩兩比較,將最大的放在最后面;
? ? ? ?2)將剩余序列中所有元素兩兩比較,將最大的放在最后面;
? ? ? ?3)重復第二步,直到只剩下一個數。
實現邏輯:
? ? ? ?1)設置循環次數;
? ? ? ?2)設置開始比較的位數,和結束的位數;
? ? ? ?3)兩兩比較,將最小的放到前面去;
? ? ? ?4)重復2、3步,直到循環次數完畢。
代碼示例:
public void bubbleSort(int[] a){int length=a.length;int temp;for(int i=0;i<a.length;i++){for(int j=0;j<a.length-i-1;j++){if(a[j]>a[j+1]){temp=a[j];a[j]=a[j+1];a[j+1]=temp;}}}}
冒泡排序算法的改進
? ? ? ?對冒泡排序常見的改進方法是加入一標志性變量exchange,用于標志某一趟排序過程中是否有數據交換,如果進行某一趟排序時并沒有進行數據交換,則說明數據已經按要求排列好,可立即結束排序,避免不必要的比較過程。本文再提供以下兩種改進算法:
? ? ? ?1、設置一標志性變量pos,用于記錄每趟排序中最后一次進行交換的位置。由于pos位置之后的記錄均已交換到位,故在進行下一趟排序時只要掃描到pos位置即可。
代碼示例:
void Bubble_1 ( int r[], int n) { int i= n -1; //初始時,最后位置保持不變 while ( i> 0) { int pos= 0; //每趟開始時,無記錄交換 for (int j= 0; j< i; j++) if (r[j]> r[j+1]) { pos= j; //記錄交換的位置 int tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp; } i= pos; //為下一趟排序作準備 }
} 代碼示例:
void Bubble_2 ( int r[], int n){ int low = 0; int high= n -1; //設置變量的初始值 int tmp,j; while (low < high) { for (j= low; j< high; ++j) //正向冒泡,找到最大者 if (r[j]> r[j+1]) { tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp; } --high; //修改high值, 前移一位 for ( j=high; j>low; --j) //反向冒泡,找到最小者 if (r[j]<r[j-1]) { tmp = r[j]; r[j]=r[j-1];r[j-1]=tmp; } ++low; //修改low值,后移一位 }
}
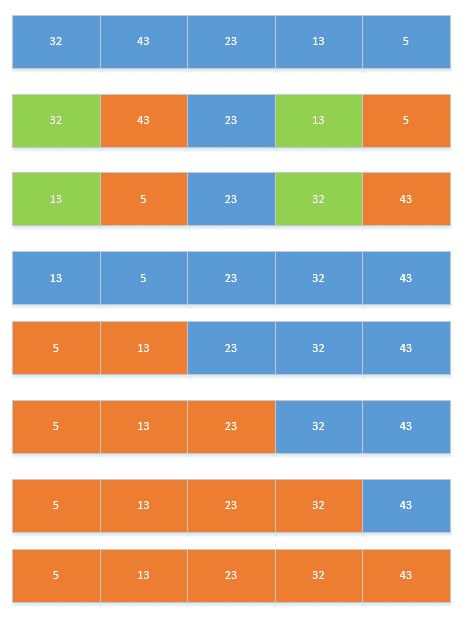
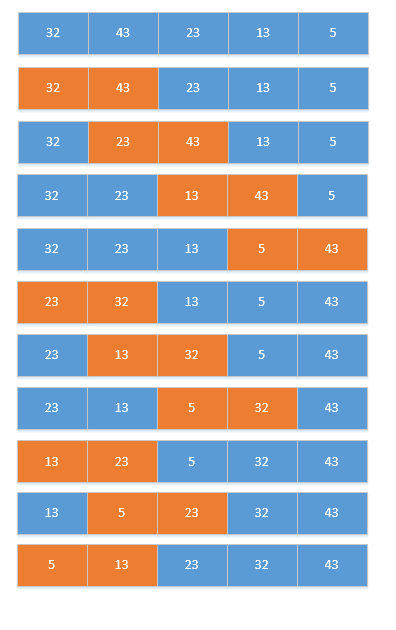
6、交換排序——快速排序
使用場景:
? ? ? ?要求時間最快時。
基本思想:
? ? ? ?1)選擇一個基準元素,通常選擇第一個元素或者最后一個元素,
? ? ? ?2)通過一趟排序講待排序的記錄分割成獨立的兩部分,其中一部分記錄的元素值均比基準元素值小。另一部分記錄的?元素值比基準值大。
? ? ? ?3)此時基準元素在其排好序后的正確位置
? ? ? ?4)然后分別對這兩部分記錄用同樣的方法繼續進行排序,直到整個序列有序。
一趟排序的過程:
排序的全過程:
代碼示例:
public static void quickSort(int[] numbers, int start, int end) { if (start < end) { int base = numbers[start]; // 選定的基準值(第一個數值作為基準值) int temp; // 記錄臨時中間值 int i = start, j = end; do { while ((numbers[i] < base) && (i < end)) i++; while ((numbers[j] > base) && (j > start)) j--; if (i <= j) { temp = numbers[i]; numbers[i] = numbers[j]; numbers[j] = temp; i++; j--; } } while (i <= j); if (start < j) quickSort(numbers, start, j); if (end > i) quickSort(numbers, i, end); }
}
分析:
? ? ? ?快速排序是通常被認為在同數量級(O(nlog2n))的排序方法中平均性能最好的。但若初始序列按關鍵碼有序或基本有序時,快排序反而蛻化為冒泡排序。為改進之,通常以“三者取中法”來選取基準記錄,即將排序區間的兩個端點與中點三個記錄關鍵碼居中的調整為支點記錄。快速排序是一個不穩定的排序方法。
快速排序的改進
? ? ? ?在本改進算法中,只對長度大于k的子序列遞歸調用快速排序,讓原序列基本有序,然后再對整個基本有序序列用插入排序算法排序。實踐證明,改進后的算法時間復雜度有所降低,且當k取值為?8?左右時,改進算法的性能最佳。
代碼示例:
void print(int a[], int n){ for(int j= 0; j<n; j++){ cout<<a[j] <<" "; } cout<<endl;
} void swap(int *a, int *b)
{ int tmp = *a; *a = *b; *b = tmp;
} int partition(int a[], int low, int high)
{ int privotKey = a[low]; //基準元素 while(low < high){ //從表的兩端交替地向中間掃描 while(low < high && a[high] >= privotKey) --high; //從high 所指位置向前搜索,至多到low+1 位置。將比基準元素小的交換到低端 swap(&a[low], &a[high]); while(low < high && a[low] <= privotKey ) ++low; swap(&a[low], &a[high]); } print(a,10); return low;
} void qsort_improve(int r[ ],int low,int high, int k){ if( high -low > k ) { //長度大于k時遞歸, k為指定的數 int pivot = partition(r, low, high); // 調用的Partition算法保持不變 qsort_improve(r, low, pivot - 1,k); qsort_improve(r, pivot + 1, high,k); }
}
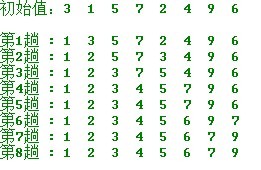
void quickSort(int r[], int n, int k){ qsort_improve(r,0,n,k);//先調用改進算法Qsort使之基本有序 //再用插入排序對基本有序序列排序 for(int i=1; i<=n;i ++){ int tmp = r[i]; int j=i-1; while(tmp < r[j]){ r[j+1]=r[j]; j=j-1; } r[j+1] = tmp; } } int main(){ int a[10] = {3,1,5,7,2,4,9,6,10,8}; cout<<"初始值:"; print(a,10); quickSort(a,9,4); cout<<"結果:"; print(a,10); }7、歸并排序
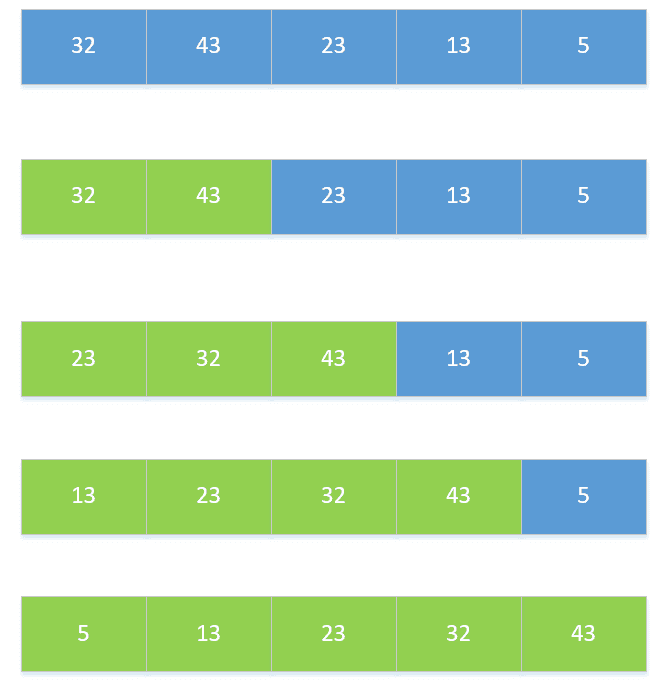
使用場景:
? ? ? ?速度僅次于快排,內存少的時候使用,可以進行并行計算的時候使用。
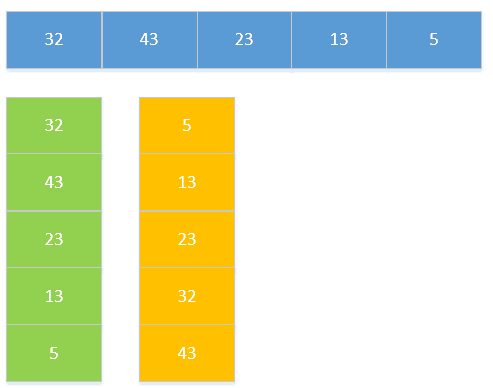
基本思想:
? ? ? ?1)選擇相鄰兩個數組成一個有序序列;
? ? ? ?2)選擇相鄰的兩個有序序列組成一個有序序列;
? ? ? ?3)重復第二步,直到全部組成一個有序序列。
實現邏輯:
設r[i…n]由兩個有序子表r[i…m]和r[m+1…n]組成,兩個子表長度分別為n-i +1、n-m。
? ? ? ?1、j=m+1;k=i;i=i; //置兩個子表的起始下標及輔助數組的起始下標;
? ? ? ?2、若i>m 或j>n,轉⑷ //其中一個子表已合并完,比較選取結束;
? ? ? ?3、//選取r[i]和r[j]較小的存入輔助數組rf
? ? ? ? ? ? ?如果r[i]<r[j],rf[k]=r[i]; i++; k++; 轉⑵
? ? ? ? ? ? ?否則,rf[k]=r[j]; j++; k++; 轉⑵
? ? ? ?4、//將尚未處理完的子表中元素存入rf
? ? ? ? ? ? ?如果i<=m,將r[i…m]存入rf[k…n] //前一子表非空
? ? ? ? ? ? ?如果j<=n , ?將r[j…n] 存入rf[k…n] //后一子表非空
? ? ? ?5、合并結束。??
代碼示例:
public static void mergeSort(int[] numbers, int left, int right) { int t = 1;// 每組元素個數 int size = right - left + 1; while (t < size) { int s = t;// 本次循環每組元素個數 t = 2 * s; int i = left; while (i + (t - 1) < size) { merge(numbers, i, i + (s - 1), i + (t - 1)); i += t; } if (i + (s - 1) < right) merge(numbers, i, i + (s - 1), right); }
}
private static void merge(int[] data, int p, int q, int r) { int[] B = new int[data.length]; int s = p; int t = q + 1; int k = p; while (s <= q && t <= r) { if (data[s] <= data[t]) { B[k] = data[s]; s++; } else { B[k] = data[t]; t++; } k++; } if (s == q + 1) B[k++] = data[t++]; else B[k++] = data[s++]; for (int i = p; i <= r; i++) data[i] = B[i];
}
歸并的迭代算法
? ? ? ?1 個元素的表總是有序的。所以對n 個元素的待排序列,每個元素可看成1 個有序子表。對子表兩兩合并生成n/2個子表,所得子表除最后一個子表長度可能為1 外,其余子表長度均為2。再進行兩兩合并,直到生成n 個元素按關鍵碼有序的表。
代碼示例:
void print(int a[], int n){ for(int j= 0; j<n; j++){ cout<<a[j] <<" "; } cout<<endl;
} //將r[i…m]和r[m +1 …n]歸并到輔助數組rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{ int j,k; for(j=m+1,k=i; i<=m && j <=n ; ++k){ if(r[j] < r[i]) rf[k] = r[j++]; else rf[k] = r[i++]; } while(i <= m) rf[k++] = r[i++]; while(j <= n) rf[k++] = r[j++]; print(rf,n+1);
} void MergeSort(ElemType *r, ElemType *rf, int lenght)
{ int len = 1; ElemType *q = r ; ElemType *tmp ; while(len < lenght) { int s = len; len = 2 * s ; int i = 0; while(i+ len <lenght){ Merge(q, rf, i, i+ s-1, i+ len-1 ); //對等長的兩個子表合并 i = i+ len; } if(i + s < lenght){ Merge(q, rf, i, i+ s -1, lenght -1); //對不等長的兩個子表合并 } tmp = q; q = rf; rf = tmp; //交換q,rf,以保證下一趟歸并時,仍從q 歸并到rf }
} int main(){ int a[10] = {3,1,5,7,2,4,9,6,10,8}; int b[10]; MergeSort(a, b, 10); print(b,10); cout<<"結果:"; print(a,10); }
代碼示例:
void MSort(ElemType *r, ElemType *rf,int s, int t)
{ ElemType *rf2; if(s==t) r[s] = rf[s]; else { int m=(s+t)/2; /*平分*p 表*/ MSort(r, rf2, s, m); /*遞歸地將p[s…m]歸并為有序的p2[s…m]*/ MSort(r, rf2, m+1, t); /*遞歸地將p[m+1…t]歸并為有序的p2[m+1…t]*/ Merge(rf2, rf, s, m+1,t); /*將p2[s…m]和p2[m+1…t]歸并到p1[s…t]*/ }
}
void MergeSort_recursive(ElemType *r, ElemType *rf, int n)
{ /*對順序表*p 作歸并排序*/ MSort(r, rf,0, n-1);
} 8、基數排序
使用場景:
? ? ? ?用于大量數,很長的數進行排序時。
基本思想:
? ? ? ?1)將所有的數的個位數取出,按照個位數進行排序,構成一個序列;
? ? ? ?2)將新構成的所有的數的十位數取出,按照十位數進行排序,構成一個序列。
代碼示例:
public void sort(int[] array) {//首先確定排序的趟數; int max = array[0];for (int i = 1; i < array.length; i++) {if (array[i] > max) {max = array[i];}}int time = 0;//判斷位數; while (max > 0) {max /= 10;time++;}//建立10個隊列; List<ArrayList> queue = new ArrayList<ArrayList>();for (int i = 0; i < 10; i++) {ArrayList<Integer> queue1 = new ArrayList<Integer>();queue.add(queue1);}//進行time次分配和收集; for (int i = 0; i < time; i++) {//分配數組元素; for (int j = 0; j < array.length; j++) {//得到數字的第time+1位數; int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);ArrayList<Integer> queue2 = queue.get(x);queue2.add(array[j]);queue.set(x, queue2);}int count = 0;//元素計數器; //收集隊列元素; for (int k = 0; k < 10; k++) {while (queue.get(k).size() > 0) {ArrayList<Integer> queue3 = queue.get(k);array[count] = queue3.get(0);queue3.remove(0);count++;}}}}
三、總結
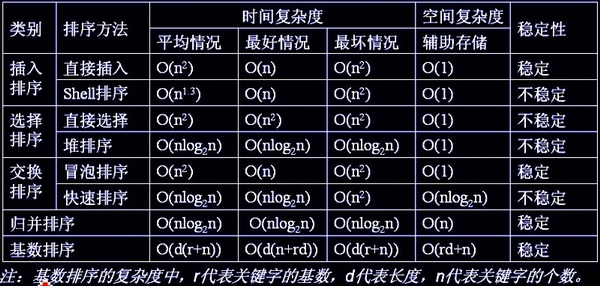
各種排序的穩定性,時間復雜度和空間復雜度總結:
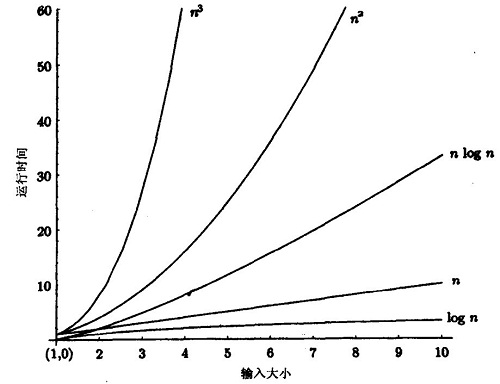
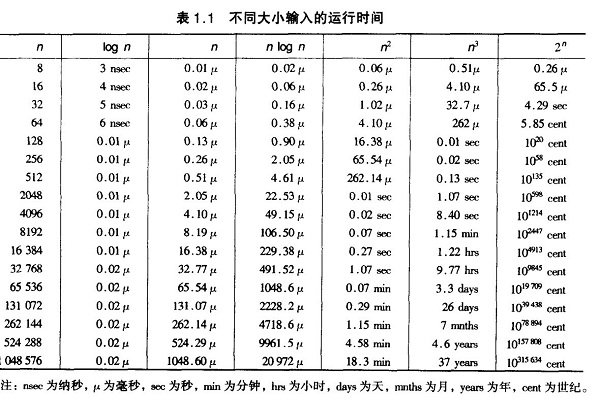
我們比較時間復雜度函數的情況:
時間復雜度函數O(n)的增長情況:
? ? ? ?所以對n較大的排序記錄。一般的選擇都是時間復雜度為O(nlog2n)的排序方法。
時間復雜度來說
(1)平方階(O(n2))排序
? ? ? ?各類簡單排序:直接插入、直接選擇和冒泡排序;
(2)線性對數階(O(nlog2n))排序
? ? ? ?快速排序、堆排序和歸并排序;
(3)O(n1+§))排序,§是介于0和1之間的常數。
? ? ? ?希爾排序
(4)線性階(O(n))排序
? ? ? ?基數排序,此外還有桶、箱排序。
說明:
? ? ? ?1)當原表有序或基本有序時,直接插入排序和冒泡排序將大大減少比較次數和移動記錄的次數,時間復雜度可降至O(n);
? ? ? ?2)而快速排序則相反,當原表基本有序時,將蛻化為冒泡排序,時間復雜度提高為O(n2);
? ? ? ?3)原表是否有序,對簡單選擇排序、堆排序、歸并排序和基數排序的時間復雜度影響不大。
穩定性
? ? ? ?排序算法的穩定性:若待排序的序列中,存在多個具有相同關鍵字的記錄,經過排序, 這些記錄的相對次序保持不變,則稱該算法是穩定的;若經排序后,記錄的相對 次序發生了改變,則稱該算法是不穩定的。?
? ? ? ?穩定性的好處:排序算法如果是穩定的,那么從一個鍵上排序,然后再從另一個鍵上排序,第一個鍵排序的結果可以為第二個鍵排序所用。基數排序就是這樣,先按低位排序,逐次按高位排序,低位相同的元素其順序再高位也相同時是不會改變的。另外,如果排序算法穩定,可以避免多余的比較。
? ? ? ?穩定的排序算法:冒泡排序、插入排序、歸并排序和基數排序。
? ? ? ?不是穩定的排序算法:選擇排序、快速排序、希爾排序、堆排序。
選擇排序算法的準則
? ? ? ?每種排序算法都各有優缺點。因此,在實用時需根據不同情況適當選用,甚至可以將多種方法結合起來使用。
選擇排序算法的依據
? ? ? ?影響排序的因素有很多,平均時間復雜度低的算法并不一定就是最優的。相反,有時平均時間復雜度高的算法可能更適合某些特殊情況。同時,選擇算法時還得考慮它的可讀性,以利于軟件的維護。一般而言,需要考慮的因素有以下四點:
? ? ? ?1、待排序的記錄數目n的大小;
? ? ? ?2、記錄本身數據量的大小,也就是記錄中除關鍵字外的其他信息量的大小;
? ? ? ?3、關鍵字的結構及其分布情況;
? ? ? ?4、對排序穩定性的要求。
設待排序元素的個數為n。
? ? ? ?1)當n較大,則應采用時間復雜度為O(nlog2n)的排序方法:快速排序、堆排序或歸并排序序。
? ? ? ? ? ? ? 快速排序:是目前基于比較的內部排序中被認為是最好的方法,當待排序的關鍵字是隨機分布時,快速排序的平均時間最短;
? ? ? ? ? ? ??堆排序:如果內存空間允許且要求穩定性的,
? ? ? ? ? ? ? 歸并排序:它有一定數量的數據移動,所以我們可能過與插入排序組合,先獲得一定長度的序列,然后再合并,在效率上將有所提高。
? ? ? ?2)當n較大,內存空間允許,且要求穩定性 =》歸并排序
? ? ? ?3)當n較小,可采用直接插入或直接選擇排序。
? ? ? ? ? ? ? 直接插入排序:當元素分布有序,直接插入排序將大大減少比較次數和移動記錄的次數。
? ? ? ? ? ? ? 直接選擇排序:元素分布有序,如果不要求穩定性,選擇直接選擇排序
? ? ? ?5)一般不使用或不直接使用傳統的冒泡排序。
? ? ? ?6)基數排序
? ? ? ? ? ? ? 基數排序是一種穩定的排序算法,但有一定的局限性:
? ? ? ? ? ? ? 1、關鍵字可分解。
? ? ? ? ? ? ? 2、記錄的關鍵字位數較少,如果密集更好
? ? ? ? ? ? ? 3、如果是數字時,最好是無符號的,否則將增加相應的映射復雜度,可先將其正負分開排序。
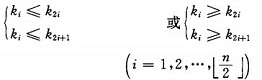









)
)











