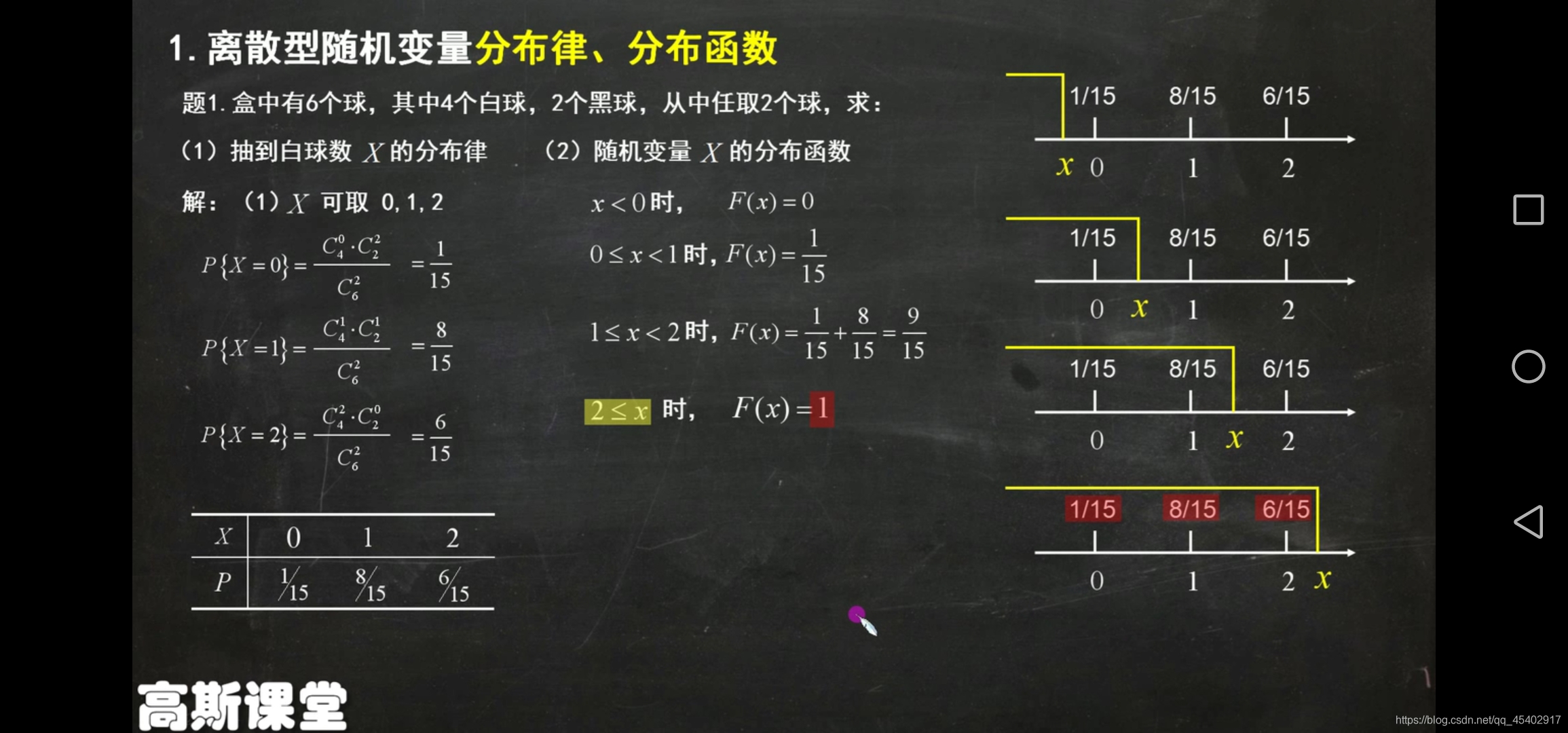
隨機變量
離散型隨機變量:有限個或無限可列個
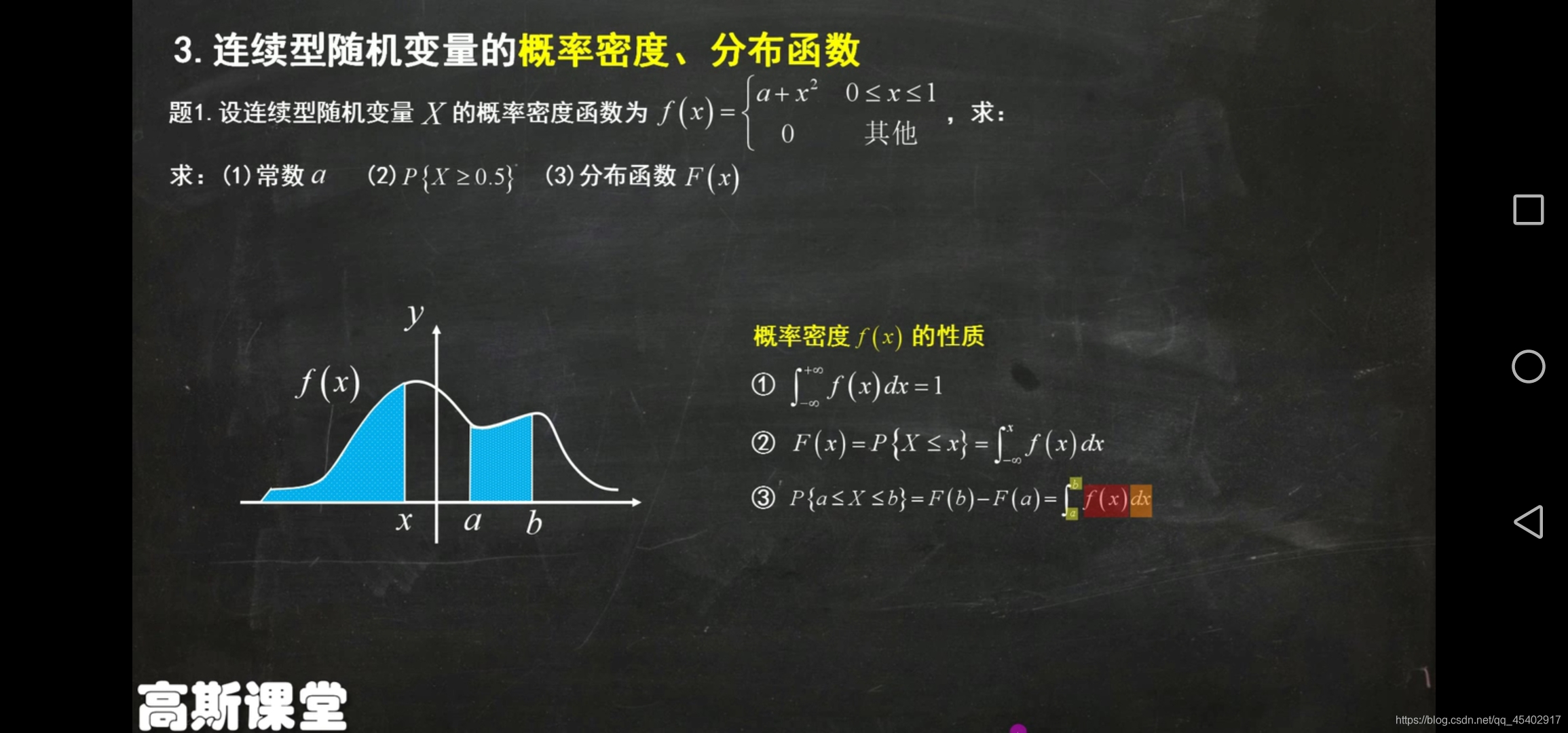
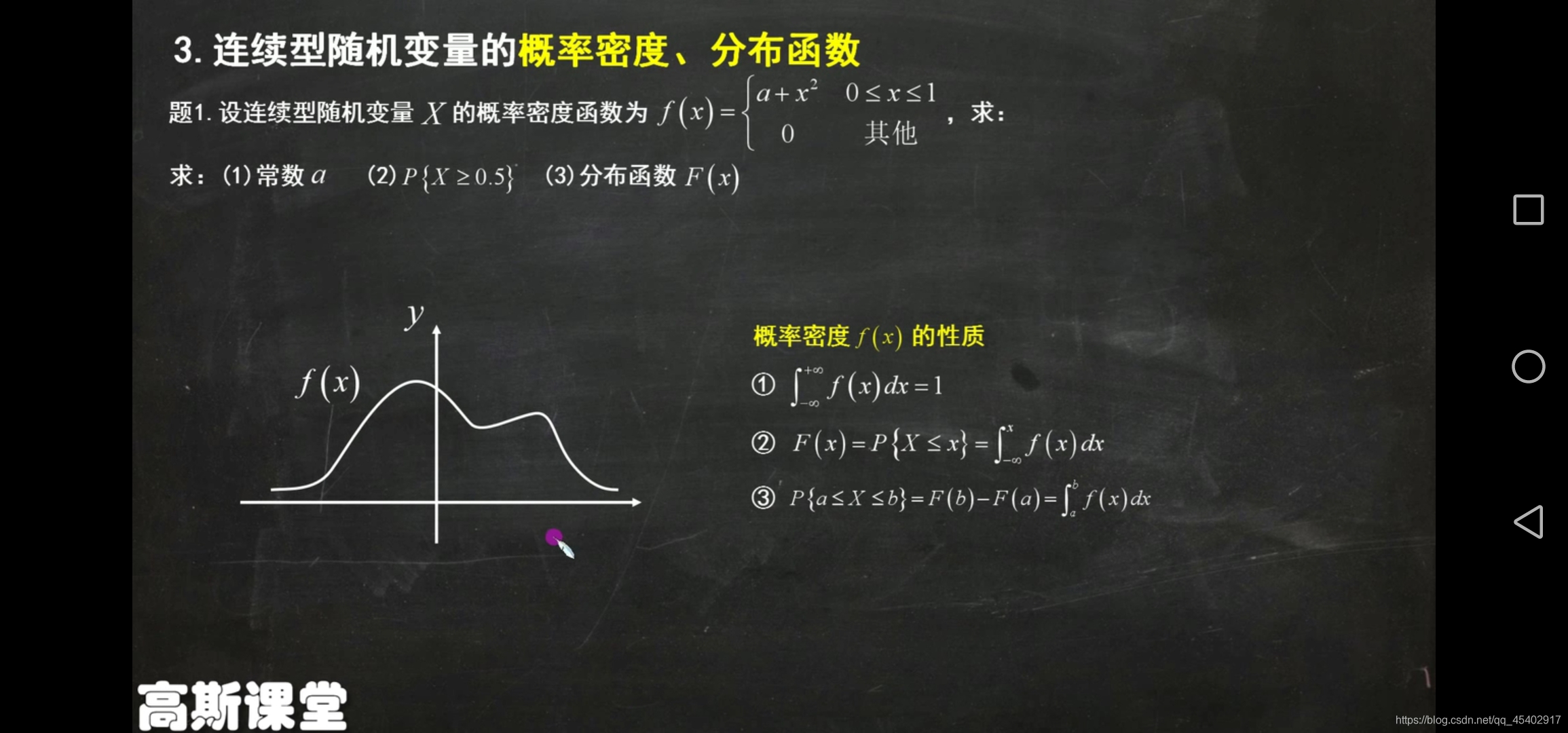
連續型隨機變量
分布函數F(X)
范圍是[a,b)
包含能取到a以及a之前的值的概率相加
分布律(概率分布)
1.所有概率相加為1
2.W=X-1,計算出每一個對應的W,然后如果有相同的W就合并其概率,最后一一對應P(x)即可
概率密度函數(密度)
1.記住負無窮到0
某個數到正無窮
2.[a,b]=(a,b)=(a,b]=[a,b)
f(x),P{x},F(x)使用時不用區分開閉區間
3.F(x)’=f(x)
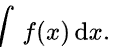
積分f(x)dx=F(x)
常見的離散型隨機變量
1.兩點分布或0-1分布
只有兩個可能的結果:A發生或不發生
2.n重伯努利事件(二項分布) X~B/b(n,p)
只有兩個可能的結果:A發生或不發生,將這個試驗獨立地進行n次
p=Cnkp^k
*(1-p)^n-k
一般將這個試驗發生的次數記為X
3.泊松分布 X~P(入)
當二項分布比較大的時候,入=np
可以Cnkp^k
*(1-p)^n-k=
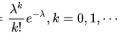

4.超幾何分布 無放回
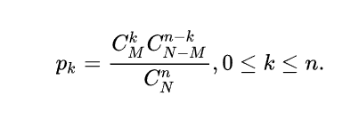
常見的連續型隨機變量
1.均勻分布 X~U(a,b)
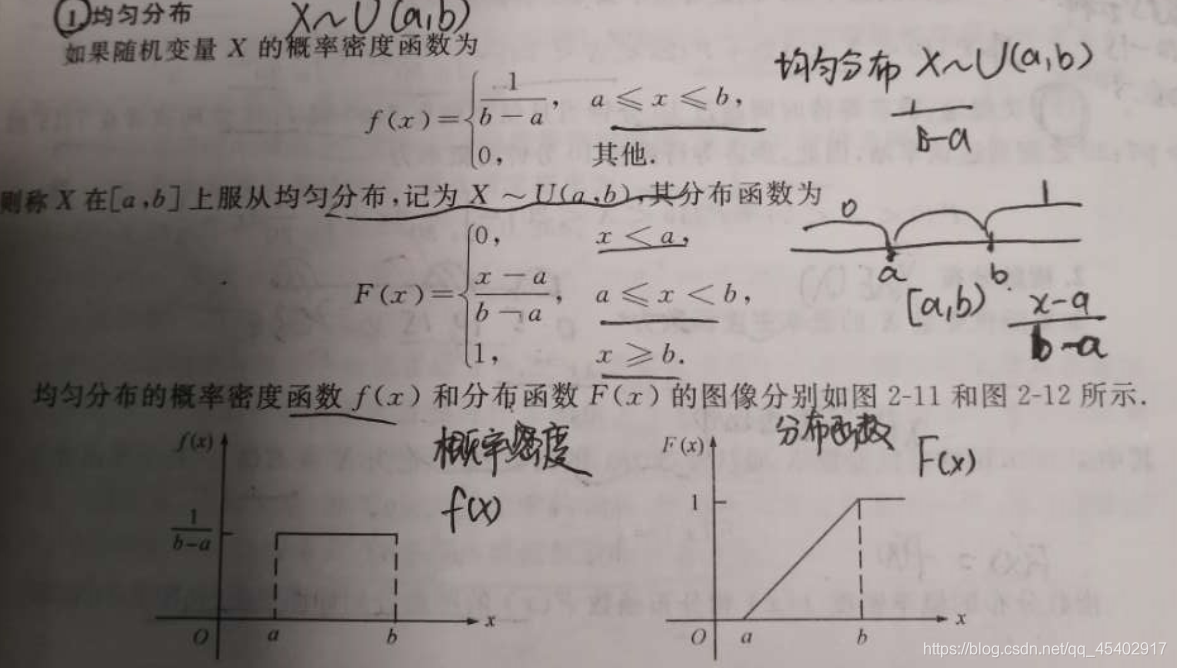

2.指數分布 X~E(入)
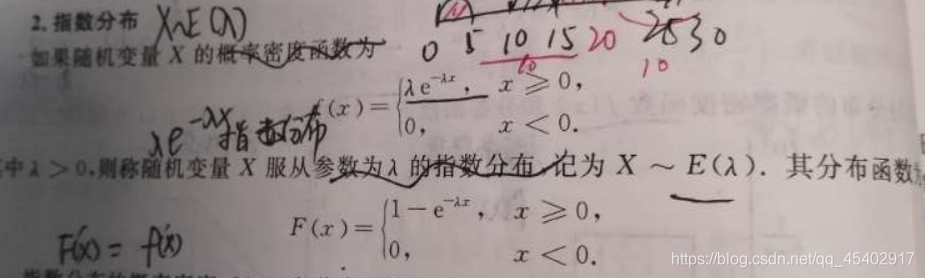
3.正態分布 X~N(μ,σ^2)
函數關于x=μ對稱
σ越大,曲線越扁平,反之,σ越小,曲線越尖
值一定落在(μ-3σ,μ+3σ)之內
4.標準正態分布 X~N(0,1)
當μ = 0,σ = 1時的正態分布是標準正態分布。

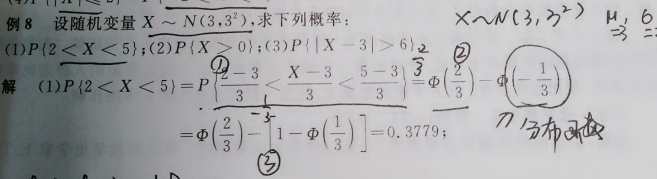
常用知識點