【相關閱讀】

【初中數學】反比例函數策略之一 ——數形結合

反比例函數策略(二)

——構造方程法

(王 橋)

上一次，咱們探討了解決反比例函數的策略一——數形結合，本節課我們繼續反比例函數的策略(二)——構造方程法。

構造方程法，在《春季攻勢》第3講有專門的講述，咱們今天重點討論下解決反比例函數的問題時，常用的“構造方程”策略。先看例題：

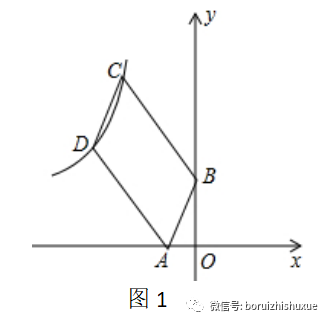
例1、如圖1，已知四邊形ABCD是平行四邊形，BC=2AB，A，B兩點的坐標分別是(-1，0)，(0，2)，C、D兩點在反比例函數y=k/x(x＜0)的圖象上，則k等于?????????.——選自《沙場秋點兵》——反比例函數中的面積問題

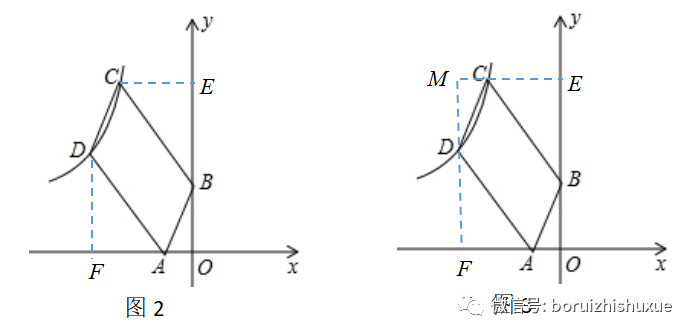
解析：欲求k，必求點C或點D的坐標；遇坐標，“做雙垂”(是不是咱上回書說到的“數形結合”？)，如圖2，作CE⊥y軸于點E，作DF⊥x軸于點F——等等，咱干脆構造“類弦圖”吧——如圖3......

方法一：特值法之——跟著感覺取特值(詳見《沖刺十招》之第1招“絕境逢生用特值”)

???數學直覺1：△DFA≌△BEC，△DMC≌△BOA；

???數學直覺2：△DFA∽△BOA∽△BEC∽△DMC；

???因為OA=1，OB=2，BC=2AB，則BE=DF=2OB=4，EC=AF=2OA=2，∴C(-2，6)，D(-3，4)，則k=-12——偷偷的看了標準答案，居然正確！

? 方法二：構造方程法

???如果說上面的“特值法”是屬于不走尋常路的“特法”，還讓我們有點忐忑不安的話(僅僅是感覺啊？三角形真的全等？相似？——但秒殺的感覺還是很爽的！！！)，咱們用“通法”——構造方程法

???見未知，設未知，找等量，造方程！而對于反比例函數來說，根據反比例函數圖像上的任意一點，縱橫坐標為定值k構造方程可是“通法”啊！

? ? ??我們先搞定全等問題。

如果您的學生知道“如果一個角的兩邊分別平行于另一個角的兩邊，這兩條邊相等或互補”，則易知∠DAF=∠BCE，則根據“AAS”易證△DFA≌△BEC，同理△DMC≌△BOA。

如果這條性質您的學生還不知道，沒關系，如圖4，延長DA，交y軸于點N，則易證明∠FDA=∠ONA=∠EBC，則易證明△DFA≌△BEC，同理△DMC≌△BOA。

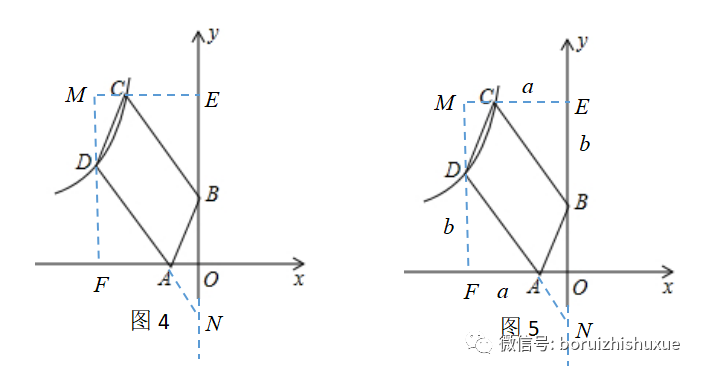
那么，這些三角形是否相似呢？不能再靠“感覺了”！

? ??? 見未知，設未知，找等量，造方程！

如圖5，不妨設AF=CE=a，DF=BE=b，則點C(-a，b+2)，D(a+1，-b)。

根據反比例函數圖像上的任意一點，縱橫坐標為定值k構造方程得：-a(b+2)=-b(a+1)，整理得b=2a，則BE:EC=BO:AO，則△BEC∽△BOA。再根據BC=2AB，得相似比為2:1，則a=2，b=4，則C(-2，6)，D(-3，4)，k=-12.

再來一道：

例2、(2010武漢)如圖6，直線y=-√3x+b與y軸交于點A，與雙曲線y=k/x在第一象限內交于兩點B、C，且AB·AC=4，則k=???????????。——選自《沙場秋點兵》——反比例函數中的常見模型

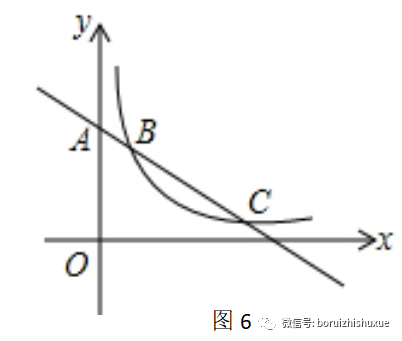
??解析：這道題目，若按照常規的解法，還是比較麻煩(前幾天還有個網友在問這道題目的解法)的。觀察到直線y=-√3x+b與y軸交于點A，不妨設直線y=-√3x+b與x軸的交點為D，則易知∠ADO=30°。則OA:OD:AD=1：√3：2。根據《沙場秋點兵》之——“反比例函數中的常見模型”中提到的策略，如圖7，則AB=CD(證明略)。

觀察到題目中的條件：AB·AC=4，根據“斜化正”的基本策略，分別過點B、C作x軸和y軸的垂線BE、BF，CM、CN。因為AB=CD，則易證△ABF≌△CDM，不妨設CM=NO=AF=a，則BF=OE=MD=√3a，AB=CD=2a。若設FN=BP=b，則PC=b，BC=2b。因為AB·AC=4，即2a·2(a+b)=4a(a+b)=4，∴a(a+b)=1。則k=BF·BE=√3a·(a+b)=√3.

評注：把未知的設出來，根據題目中的條件構造方程——這里指“2a·2(a+b)=4a(a+b)=4”，再根據反比例函數圖像上任意一點的縱橫坐標的乘積為定值k的事實進行整體代換，這種“設而不求”“整體代換”的策略很耐人尋味。

下面這兩道題，咱們下去練練，體會一下“構造方程法”的妙處！系統的“構造方程法”的講解，請參閱一輪培優教材《春季攻勢》第3講——構造方程法！

1、(2018遵義)如圖8，直角三角形的直角頂點在坐標原點，∠OAB=30°，若點A在反比例函數y=6/6(x＞0)的圖象上，則經過點B的反比例函數解析式為(　　)——選自《沙場秋點兵》——反比例函數與特殊的幾何圖形

? ?? A．y=-6/x ???B．y=-4/x??C．y=-2/x ??D．y=2/x

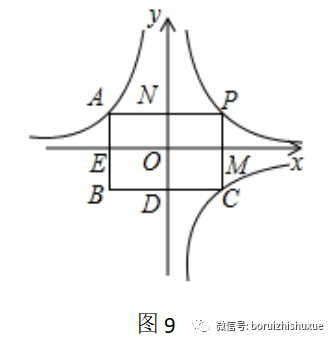
2、如圖9，兩個反比例函數y1=k1/x1和y2=k2/x2(其中k₁＞0＞k₂)在第一象限內的圖象是C₁，第二、四象限內的圖象是C₂，設點P在C₁上，PC⊥x軸于點M，交C₂于點C，PA⊥y軸于點N，交C₂于點A，AB∥PC，CB∥AP相交于點B，則四邊形ODBE的面積為(　　)——選自《沙場秋點兵》——反比例函數中的面積問題

A.?|k1﹣k2| ?????B.k1/?|k2|?????????C.?|k1?k2|??????D.K₂²/k₁?

3、如圖10—1，已知直線y=1/2x與雙曲線y=k/x交于A、B兩點，且點A的橫坐標為4．(1)求k的值；(2)如圖10—2，過原點O的另一條直線l交雙曲線y=k/x于C、D兩點(點C在第一象限且在點A的左邊)，當四邊形ACBD的面積為24時，求點C的坐標．——選自《沙場秋點兵》——反比例函數中的常見模型

【來源】 播睿智數學。

【相關閱讀】(點擊藍色字體查看)

許興華——從有爭議的y=5log6(x)是否為對數函數談起

趙振華——剖析一道強基培訓試題的解法

彭西東——拋物線最好題源：阿基米德三角形

中科院席南華院士：數學的意義

【中考研究】“飛魚模型” ——相似三角形的一個常見二級模型

【廣州中考】2001年廣東省廣州市中考數學試卷及詳細解答

【初中數學】等角的存在性問題

【初中數學】二次函數之正方形存在性問題

【初中數學】動態演示：旋轉變換之捆綁變換

【中考數學】精彩紛呈的一題多解

【中考數學】2020中考數學相似模型大全

【初中數學】動態演示：旋轉變換之捆綁變換

【中考研究】24道最新中考數學壓軸題詳細解析

【初中數學】利用一元二次方程解實際問題

【初中數學】"燕尾模型解決面積問題"引發的思考

初高中銜接：因式分解的13種方法，必須掌握！

【投稿須知】公眾號《許興華數學》誠邀全國各地中小學數學教師、教研員和數學愛好者熱情投稿！來稿時請注意以下五點：(1)來稿請注明真實姓名、工作單位、聯系方式(無具體工作單位和真實姓名的投稿，一般都不會采用)。

(2)來稿一般要求同時用word文檔和PDF格式的電子稿件(防止不同版本的Word打開時出現亂碼)。另外，也接受少數著名教師的手寫稿(手寫稿必須清晰可讀)。

(3)每篇文章請認真審查復核，防止錯誤發生，來稿文責自負。如有抄襲，則有可能被舉報并受到有關著作版權部門的追責。
(4)投稿郵箱：chinamatha@163.com；或加主編微信xuxinghua168投稿.

(5)本公眾號對優秀作者和名師一般會附上“作者簡介”，以讓廣大讀者更好地了解作者的研究成果和方向，以便進一步學習作者的相關數學思想或解題方法。