r語言隨機森林回歸預測_從零實現回歸隨機森林

一、前言

回歸隨機森林作為一種機器學習和數據分析領域常用且有效的算法，對其原理和代碼實現過程的掌握是非常有必要的。為此，本文將著重介紹從零開始實現回歸隨機森林的過程，對于隨機森林和決策樹的相關理論原理將不做太深入的描述。本文的目的只是為了演示回歸隨機森林主要功能的具體實現過程，在實現過程中不會考慮代碼性能，會更加注重代碼可讀性。

實現語言：Python

依賴：pandas, numpy

二、原理介紹

隨機森林屬于Bagging類算法，而Bagging 又屬于集成學習一種方法（集成學習方法大致分為Boosting和Bagging方法，兩個方法的不同請參考[10]），集成學習的大致思路是訓練多個弱模型打包起來組成一個強模型，強模型的性能要比單個弱模型好很多（三個臭皮匠頂一個諸葛亮。注意：這里的弱和強是相對的），其中的弱模型可以是決策樹、SVM等模型，在隨機森林中，弱模型選用決策樹。

在訓練階段，隨機森林使用bootstrap采樣從輸入訓練數據集中采集多個不同的子訓練數據集來依次訓練多個不同決策樹；在預測階段，隨機森林將內部多個決策樹的預測結果取平均得到最終的結果。本文主要介紹回歸隨機森林從零實現的過程，實現的RFR(回歸隨機森林)具有以下功能：

模型訓練
模型數據預測
計算feature importance

2.1 模型訓練

2.1.1 基礎理論

本文實現的RFR是將多個二叉決策樹（即CART，這也是sklearn,spark內部實現的模型）打包組合而成的，訓練RFR便是訓練多個二叉決策樹。在訓練二叉決策樹模型的時候需要考慮怎樣選擇切分變量(特征）、切分點以及怎樣衡量一個切分變量、切分點的好壞。針對于切分變量和切分點的選擇，本實現采用窮舉法，即遍歷每個特征和每個特征的所有取值，最后從中找出最好的切分變量和切分點；針對于切分變量和切分點的好壞，一般以切分后節點的不純度來衡量，即各個子節點不純度的加權和

，其計算公式如下：

(2-1)

其中，

為某一個切分變量，

為切分變量的一個切分值，

分別為切分后左子節點的訓練樣本個數、右子節點的訓練樣本個數以及當前節點所有訓練樣本個數，

分為左右子節點的訓練樣本集合，

為衡量節點不純度的函數(impurity function/criterion)，分類和回歸任務一般采用不同的不純度函數，在分類和回歸常采用的不純度函數有以下四種：

圖 1. 四種不同的impurity function

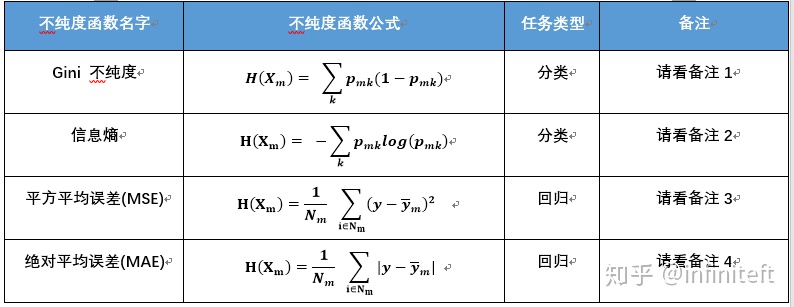
備注1：

Gini不純度只適用于分類任務，

為當前節點的訓練樣本集合，

為當前節點訓練樣本中目標變量取值k(

)出現的概率。

備注2：

信息熵只適用于分類任務，其他同備注1。

備注3

MSE只適用于回歸任務，

為當前節點樣本目標變量的平均值。

備注4

MAE只適用于回歸任務，

為當前節點樣本目標變量的平均值。

備注5

在sklearn內部，DecisionTreeClassifier, RandomForestClassifier等基于決策樹的分類模型默認使用'gini'作為impurity function，也可通過criterion參數指定為'entropy' ；而DecisionTreeRegressor, RandomForestRegressor等基于決策樹的回歸模型默認使用'mse'作為impurity function，也可通過criterion參數指定為'mae'。

決策樹中某一節點的訓練過程在數學等價于下面優化問題：

(2-2)

即尋找

最小的切分變量和切分點。

在本文實現的回歸隨機森林中，

選用MSE，即針對某一切分點

(2-3)

2.1.2 訓練過程

RFR訓練過程示意圖如圖2所示。

圖 2. RFR訓練示意圖

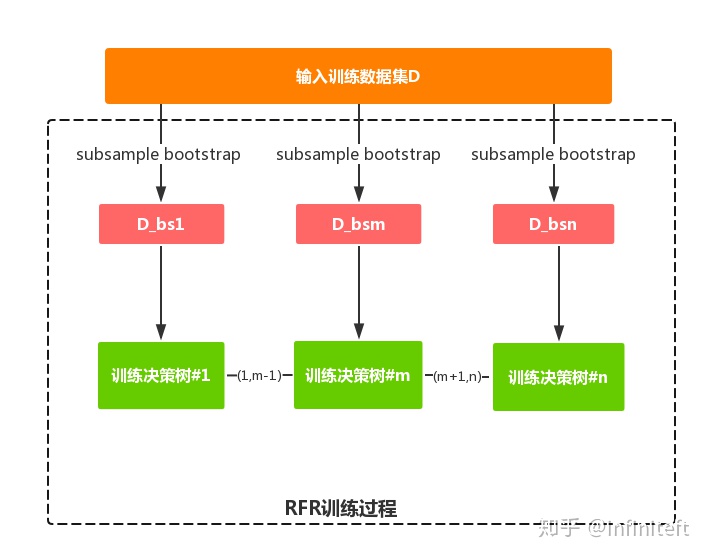
說明：

bootstrap[1]是對輸入訓練樣本集合
進行
N次放回重復抽樣得到樣本集合
(
N一般等于
的大小[2]，具體可以查看
sklearn的實現代碼)，這暗示了
中的某些樣本會在
中重復出現多次。在對
進行bootstrap采樣時，
中每個樣本會以
63.3%的概率被抽中。為什么是63.3%？考慮N次放回重復抽樣，每次抽樣每個樣本被選中的概率為
，進行N次抽樣，被選中概率為：

(2-4)

具體可以參考[3-4]。

subsample會根據輸入參數sample_sz的大小從
中采樣
sample_sz個樣本組成subsample樣本集合
(在
sklearn中，subsample大小就是輸入訓練樣本集合
的大小N，不可以通過輸入參數指定subsample的大小，詳見這里)。

為什么要進行bootstrap? 集成學習（包括隨機森林）的目的是為了使用多個不同的子模型來增加最終模型預測結果的魯棒性和穩定性(即減小方差)，如果多個子模型都采用同樣的數據集訓練，那么訓練得出的子模型都是相同的，集成學習將變得沒有意義，為了能從原輸入訓練數據集得到多個不同的數據集，需要使用bootstrap來從原數據集采樣出不同的子數據集來訓練子模型。

圖2中n個回歸決策樹的訓練過程如圖3所示。

圖 3. 回歸決策樹訓練過程

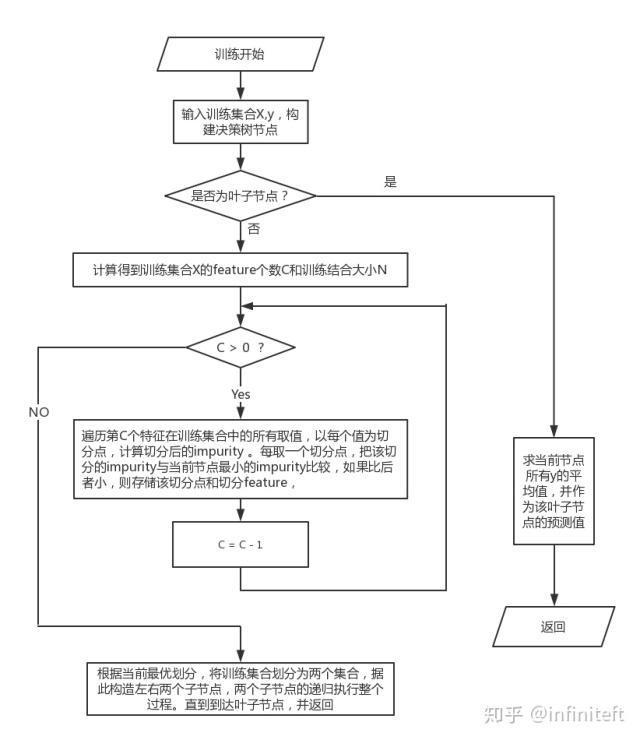
2.2 模型預測

RFR的預測結果是由內部所有二叉決策樹的預測結果取平均值得到的。二叉決策樹的預測過程主要分為以下步驟：

針對某一輸入樣本，從二叉決策樹的根節點起，判斷當前節點是否為葉子節點，如果是則返回葉子節點的預測值(即當前葉子中樣本目標變量的平均值），如果不是則進入下一步；
根據當前節點的切分變量的和切分值，將樣本中對應變量的值與節點的切分值對比。如果樣本變量值小于等于當前節點切分值，則訪問當前節點的左子節點；如果樣本變量值大于當前節點切分值，則訪問當前節點的右子節點；
循環步驟2，直到訪問到葉子節點，并返回葉子節點的預測值。

2.3 計算feature importance

特征的重要性表示特征對預測結果影響程度，某一特征重要性越大，表明該特征對預測結果的影響越大，重要性越小，表明該特征對預測結果越小。RFR中某一特征的重要性，是該特征在內部所有決策樹重要性的平均值，而在決策樹中，計算某一個特征的重要性可以采用以下三種方法：

方法1

步驟如下：

使用訓練數據訓練模型；
計算訓練數據在模型上依據某一metric的score，記為
（在回歸中，可以選用r2）；
遍歷訓練數據集中的每一個feature，每次在原訓練數據集的基礎上將對應的feature進行shuffle操作，然后使用模型得到shuffle后數據集的score，記為
，最后通過
計算出第
個feature的重要性。

方法2

如果一個feature很重要，那么從數據集中去除該feature后，模型的prediction error會增大；相反，如果一個feature不重要，那么從數據集中去除后，模型的prediction error不會變化太大。該方法的步驟如下：

使用原數據集訓練模型，并評估模型在訓練數據集上的prediction error，記為
;
遍歷訓練數據集中的每一個feature，每次從原訓練數據集的基礎上去除該feature，然后使用得到數據集訓練模型，最終計算出prediction error，記為
，最后通過
計算出第
個feature的重要性。

該方法和方法1有點類似，但該方法在計算每個feature的重要性的時候都需要重新訓練模型，會增加額外的計算量，在實際應用一般不采用該方法。

方法3

該方法是sklearn內部樹模型計算feature重要性時采用的方法。即某一節點

的重要性為

(2-5)

其中，

分別為節點

以及其左右子節點中訓練樣本個數與總訓練樣本數目的比例，

分為為節點

以及其左右子節點的不純度。知道每一個節點的重要性之后，即可通過公式(2-6)得出某一feature的重要性。

(2-6)

為了使所有feature的重要性加起來等于1，需要每一feature的重要性進行normalization，即公式(2-7)

(2-7)

方法3在sklearn中的實現，請查看_tree.pyx。

在本文實現的RFR中，同時實現了方法1和方法3。

三、回歸隨機森林實現

3.1 代碼

代碼有點長，不想看的可以直接跳過。

from multiprocessing import Pool, cpu_countclass RFRegressor(object):"""Random Forest Regressor"""def __init__(self, n_trees, sample_sz, min_leaf_sz=5, n_jobs=None, max_depth=None):self._n_trees = n_treesself._sample_sz = sample_szself._min_leaf_sz = min_leaf_szself._n_jobs = n_jobsself._max_depth = max_depthself._trees = [self._create_tree() for i in range(self._n_trees)]def _get_sample_data(self, bootstrap=True):"""Generate training data for each underlying decision treeParameters----------bootstrap: boolean value, True/FalseThe default value is True, it would bootstrap sample from input training data. If False, the exclusive sampling willbe performed.Returns-------idxs: array-like objectReturn the indices of sampled data from input training data"""if bootstrap:idxs = np.random.choice(len(self._X), self._sample_sz)else:idxs = np.random.permutation(len(self._X))[:self._sample_sz]return idxsdef _create_tree(self):"""Build decision treeeReturns-------dtree : DTreeRegressor object"""return DTreeRegressor(self._min_leaf_sz, self._max_depth)def _single_tree_fit(self, tree):"""Fit the single underlying decision treeParameters----------tree : DTreeRegressor objectReturns-------tree : DTreeRegressor object"""sample_idxs = self._get_sample_data()return tree.fit(self._X.iloc[sample_idxs], self._y[sample_idxs])def fit(self, x, y):"""Train a forest regressor of trees from the training set(x, y)Parameters----------x : DataFrame,The training input samples.y : Series or array-like objectThe target values."""self._X = xself._y = yif self._n_jobs:self._trees = self._parallel(self._trees, self._single_tree_fit, self._n_jobs)else:for tree in self._trees:self._single_tree_fit(tree)def predict(self, x):"""Predict target values using trained modelParameters---------x : DataFrame or array-like objectinput samplesReturns-------ypreds : array-like objectpredicted target values"""all_tree_preds = np.stack([tree.predict(x) for tree in self._trees]) return np.mean(all_tree_preds, axis=0)def _parallel(self, trees, fn, n_jobs=1):"""Parallel jobs executionParameters----------trees : list-like objecta list-like object contains all underlying treesfn : function-like objectmap functionn_jobs : integerThe number of jobs.Returns-------result : list-like objecta list-like result object for each call of map function `fn`"""try:workers = cpu_count()except NotImplementedError:workers = 1if n_jobs:workders = n_jobspool = Pool(processes=workers)result = pool.map(fn, trees)return list(result)@propertydef feature_importances_(self):"""Calculate feature importanceReturns-------self._feature_importances : array-like objectthe importance score of each feature """if not hasattr(self, '_feature_importances'):norm_imp = np.zeros(len(self._X.columns))for tree in self._trees:t_imp = tree.calc_feature_importance()norm_imp = norm_imp + t_imp / np.sum(t_imp)self._feature_importances = norm_imp / self._n_treesreturn self._feature_importances@propertydef feature_importances_extra(self):"""Another method to calculate feature importance"""norm_imp = np.zeros(len(self._X.columns))for tree in self._trees:t_imp = tree.calc_feature_importance_extra()norm_imp = norm_imp + t_imp / np.sum(t_imp)norm_imp = norm_imp / self._n_treesimp = pd.DataFrame({'col':self._X.columns, 'imp':norm_imp}).sort_values('imp', ascending=False)return impclass DTreeRegressor(object):def __init__(self, min_leaf_sz, max_depth=None):self._min_leaf_sz = min_leaf_szself._split_point = 0self._split_col_idx = 0self._score = float('inf')self._sample_sz = 0self._left_child_tree = Noneself._right_child_tree = Noneself._feature_importances = []self._node_importance= 0if max_depth is not None:max_depth = max_depth - 1self._max_depth = max_depthdef fit(self, x, y):self._X = xself._y = yself._col_names = self._X.columnsself._feature_importances = np.zeros(len(self._col_names))self._sample_sz = len(self._X)self._val = np.mean(self._y)if self._max_depth is not None and self._max_depth < 2:return selfself._find_best_split()return selfdef _calc_mse_inpurity(self, y_squared_sum, y_sum, n_y):"""Calculate Mean Squared Error impurityThis is just the recursive version for calculating varianceParameters----------y_squared_sum: float or int , the sum  of y squared y_sum: float or int , the sum of y valuen_y: int, the number of samplesReturns-------"""dev = (y_squared_sum / n_y) - (y_sum / n_y) ** 2return devdef _find_best_split(self):for col_idx in range(len(self._col_names)):self._find_col_best_split_point(col_idx)self._feature_importances[self._split_col_idx] = self._node_importanceif self.is_leaf:return left_child_sample_idxs = np.nonzero(self.split_col <= self.split_point)[0]right_child_sample_idxs = np.nonzero(self.split_col > self.split_point)[0]self._left_child_tree = (DTreeRegressor(self._min_leaf_sz, self._max_depth).fit(self._X.iloc[left_child_sample_idxs], self._y[left_child_sample_idxs]))self._right_child_tree = (DTreeRegressor(self._min_leaf_sz, self._max_depth).fit(self._X.iloc[right_child_sample_idxs], self._y[right_child_sample_idxs]))def _find_col_best_split_point(self, col_idx):x_col = self._X.values[:, col_idx]sorted_idxs = np.argsort(x_col)sorted_x_col = x_col[sorted_idxs]sorted_y =  self._y[sorted_idxs]lchild_n_samples = 0lchild_y_sum  = 0.0lchild_y_square_sum = 0.0rchild_n_samples = self._sample_szrchild_y_sum = sorted_y.sum()rchild_y_square_sum = (sorted_y ** 2).sum()node_y_sum = rchild_y_sumnode_y_square_sum = rchild_y_square_sum for i in range(0, self._sample_sz - self._min_leaf_sz):xi, yi = sorted_x_col[i], sorted_y[i]rchild_n_samples -= 1rchild_y_sum -= yirchild_y_square_sum -= (yi ** 2)lchild_n_samples  +=  1lchild_y_sum += yilchild_y_square_sum += (yi ** 2)if i < self._min_leaf_sz  or xi == sorted_x_col[i+1]:continuelchild_impurity = self._calc_mse_inpurity(lchild_y_square_sum,lchild_y_sum, lchild_n_samples)rchild_impurity = self._calc_mse_inpurity(rchild_y_square_sum,rchild_y_sum, rchild_n_samples)split_score  = (lchild_n_samples * lchild_impurity + rchild_n_samples * rchild_impurity) / self._sample_szif split_score < self._score:self._score = split_scoreself._split_point = xiself._split_col_idx = col_idxself._node_importance = (self._sample_sz * (self._calc_mse_inpurity(node_y_square_sum, node_y_sum, self._sample_sz) - split_score))def predict(self, x):if type(x) == pd.DataFrame:x = x.valuesreturn np.array([self._predict_row(row) for row in x])def _predict_row(self, row):if self.is_leaf:return self._valt = (self._left_child_tree if row[self._split_col_idx] <= self.split_point else self._right_child_tree)return t._predict_row(row)def __repr__(self):pr =  f'sample: {self._sample_sz}, value: {self._val}rn'if not self.is_leaf:pr += f'split column: {self.split_name}, split point: {self.split_point}, score: {self._score} 'return prdef calc_feature_importance(self):if self.is_leaf:return self._feature_importancesreturn (self._feature_importances + self._left_child_tree.calc_feature_importance()+ self._right_child_tree.calc_feature_importance())def calc_feature_importance_extra(self):imp = []o_preds = self.predict(self._X.values)o_r2 = metrics.r2_score(self._y, o_preds)for col in self._col_names:tmp_x = self._X.copy()shuffle_col = tmp_x[col].valuesnp.random.shuffle(shuffle_col)tmp_x.loc[:,col] = shuffle_coltmp_preds = self.predict(tmp_x.values)tmp_r2 = metrics.r2_score(self._y, tmp_preds)imp.append((o_r2 - tmp_r2))imp = imp / np.sum(imp)return imp@propertydef split_name(self):return self._col_names[self._split_col_idx]@propertydef split_col(self):return self._X.iloc[:, self._split_col_idx]@propertydef is_leaf(self):return self._score == float('inf')@propertydef split_point(self):return self._split_point

3.2 測試

訓練與預測：

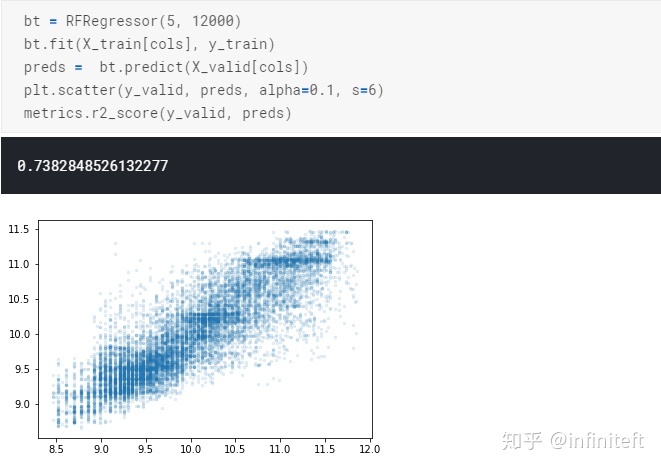
使用sklearn內部的RandomForestRegressor的結果：

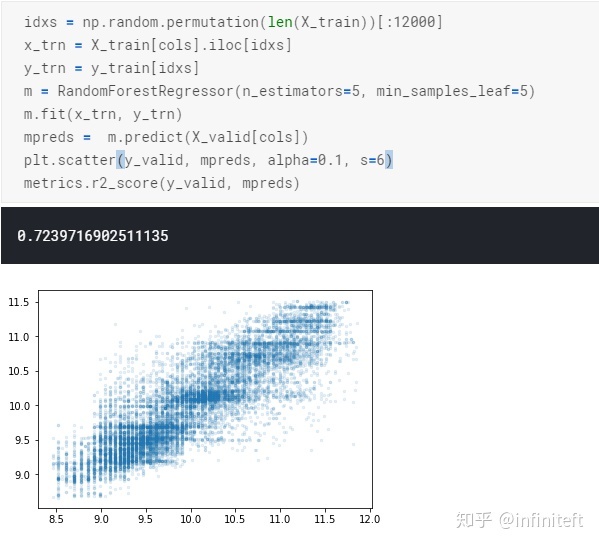
需要注意的是，上面兩次訓練的樣本不同，所以和實際情況有點出入，但大體趨勢是對。

feature importance:

RFRegressor采用方法3計算的feature重要性：

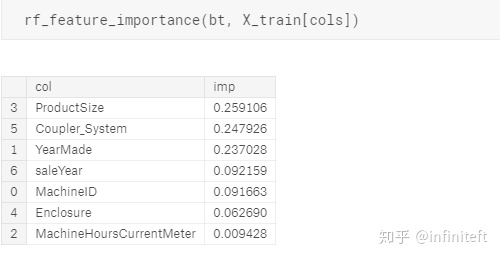
RandomForestRegressor計算的feature重要性：

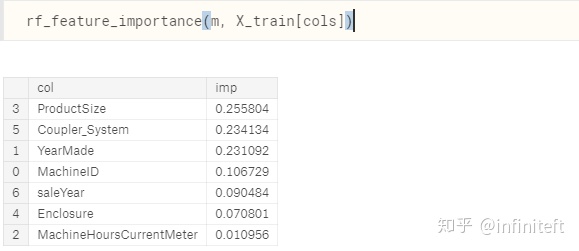
RFRegressor采用方法1計算的feature重要性：

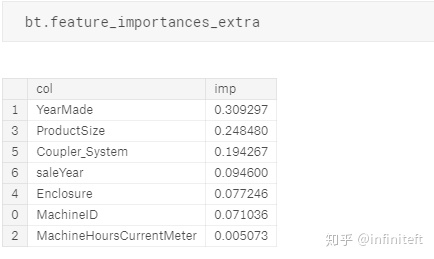
參考與薦讀：

[1] Bootstrap Sample: Definition, Example
[2] Number of Samples per-Tree in a Random Forest
[3] Why on average does each bootstrap sample contain roughly two thirds of observations?
[4] Random Forests out-of-bag sample size
[5] Random Forests Leo Breiman and Adele Cutler
[6] Why is Random Forest with a single tree much better than a Decision Tree classifier?
[7] Winning the bias-variance tradeoff
[8] subsample-bootstrapping
[9] How can SciKit-Learn Random Forest sub sample size may be equal to original training data size?
[10] the difference between bagging and boosting
[11] The Mathematics of Decision Trees, Random Forest and Feature Importance in Scikit-learn and Spark
[12] Sklearn Decision Trees documentation