題目

0,1,2…,n-1這n個數字排成一個圓圈，從數字0開始，每次從這圓圈你刪除第m個數字。求出這個圓圈里剩下的最后一個數字。

例如，0、1、2、3、4這5個數字組成一個圓圈，從數字0開始每次刪除第3個數字，則刪除的前4個數字依次2、0、4、1，因此最后剩下的數字是3。

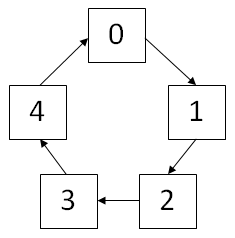
本題就是有名的約瑟夫（Josephuse）環問題。

分析

兩種解題方法：

1. 用環形鏈表模擬圓圈的經典解法
2. 分析每次被刪除的數字的規律并直接計算出圓圈中最后剩下的數字

放碼

一

用環形鏈表模擬圓圈的經典解法

public int lastRemaining(int n, int m) {if(n < 1 || m < 1) {throw new IllegalArgumentException();}LinkedList<Integer> list = new LinkedList<>();for(int i = 0; i < n; i++) {list.add(i);}int count = 0, index = 0;while(list.size() > 1) {count++;if(count == m) {list.remove(index);count = 0;}else {index++;}if(index == list.size()) {index = 0;}}return list.get(0);
}

二

分析每次被刪除的數字的規律并直接計算出圓圈中最后剩下的數字

首先我們定義一個關于 n 和 m 的方程f(n,m)，表示每次在 n 個數字 0，1， … ，n-1中每次刪除第 m 個數字最后剩下的數字。

在這 n個數字中，第一個被刪除的數字是(m-1)%n。為了簡單起見，我們把(m- 1)%n 記為 k，那么刪除k之后剩下的 n-1 個數字為 0，1，… ，k-1，k+1，… ，n-1，并且下一次刪除從數字 k+1 開始計數。相當于在剩下的序列中， k+1 排在最前面，從而形成 k+1，… ，n- 1，0，1，… ，k-1 。

該序列最后剩下的數字也應該是關于 n 和 m 的函數。由于這個序列的規律和前面最初的序列不一樣（最初的序列是從 0 開始的連續序列），因此該函數不同于前面的函數，記為 f’(n-1,m)。

最初序列最后剩下的數字 f(n, m）一定是刪除一個數字之后的序列最后剩下的數字，即 f(n, m)=f'(n-1, m）。

接下來我們把剩下的這 n-1 個數字的序列 k-1， …，n-1，0，1，… ，k-1 做一個映射，映射的結果是形成一個從 0 到 n-2 的序列：

last index	->	index
k+1		0
k+2		1
…		…
n-1		n-k-2
0		n-k-1
1		n-k
…		…
k-1		n-2

我們把映射定義為p，則p(x)=(x-k-1)%n if p(x)<0, then p(x)+=n。

它表示如果映射前的數字是x，那么映射后的數字是(x-k-1)%n。該映射的逆映射是p?1(x)=(x+k+1)%n。

由于映射之后的序列和最初的序列具有同樣的形式，即都是從0開始的連續序列，因此仍然可以用函數f來表示，記為f(n-1, m)。根據我們的映射規則，映射之前的序列中最后剩下的數字f'(n-1, m)=p?1[f(n-1, m)]=[f(n - 1, m) + k + 1] % n,把k = (m - 1) % n代入得到f(n, m)=f'(n-1, m)=[f(n-1, m) + m] % n。

經過上面復雜的分析，我們終于找到了一個遞歸公式。要得到n個數字的序列中最后剩下的數字，只需要得到n-1個數字的序列中最后剩下的數字，并以此類推。當n=1時，也就是序列中開始只有一個數字0，那么很顯然最后剩下的數字就是0。我們把這種關系表示為:

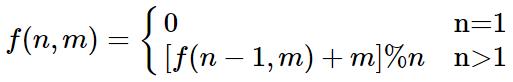
public int lastRemaining2(int n, int m) {if(n < 1 || m < 1) {throw new IllegalArgumentException();}return n == 1 ? 0 : (lastRemaining2(n - 1, m) + m) % n;
}

三

針對這個題目，先說說難點：

數字組成是環形的結構，當數到最后個數字時，還不是需要刪除的第 m 個數，需要回至數組的首位繼續；
每次重新數的位置，都是上次刪除數字的下一位。
針對第一個難點，可以考慮取模；

針對第二個難點，可以考慮將刪除數字下一位，作為下次重新數的起點，剩余數字依次排列。（注意數字組成是環狀的）

考慮先模擬，然后再進行逆推：

（為體現閉環，這里將數組進行復制。注意： 未得到最后 1 位數時，除第 1 輪開始 ，每一輪都是以上一輪刪除數字下一位作為起點，重新數需要刪除的第 m 個數）

這就是模擬之后得到的結果。

現在我們來進行逆推：

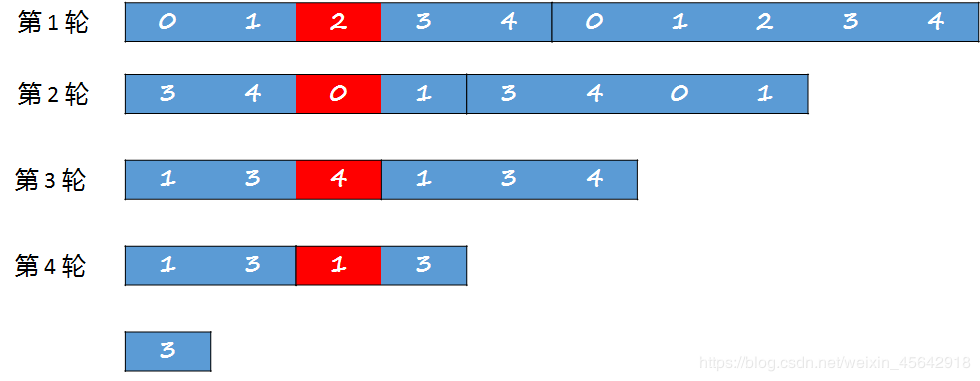
最終確定的 1 個數字，這個數字對應的索引一定是 0，逆推這個最終數字在每一輪中所處的索引位置，那么假設（n 表示數組元素個數，m 表示要刪除的第 m 個數，取示例 1，n = 5， m = 3）：

• n = 1 時，索引：0；
• n = 2 時，索引：(0 + m) % 2 = 3 % 2 = 1；
• n = 3 時，索引：((0 + m) % 2 + 3) % 3 = (1 + 3) % 3 = 1；
• n = 4 時，索引：(((0 + m) % 2 + 3) % 3 + m) % 4 = (1 + 3) % 4 = 0；
• n = 5 時，索引：((((0 + m) % 2 + 3) % 3 + m) % 4 + m) % 5 = (0 + 3) % 5 = 3 。

大致講下前面的逆推過程，找出剩余元素在前面每一輪所處的位置：

• 當剩下 1 個數字的時候，這個數字（3）的索引為 0；
• 往前逆推，當剩下 2 個數字的時候，在上一輪元素索引的基礎上，要補上 m 個位置，然后對數組元素個數取模，得到這一輪該元素所在的位置，代入 n，m，可得數字（3）索引為 1；
• 當剩下 3 個數字時，同樣補上 m 個位置，然后對數組元素個數取模（這個時候數組元素個數為 3），代入 m，n，得數字（3）索引為 1；
• …

對上面的逆推過程進行總結：從最后 1 輪往前逆推時，前面一輪的元素所處的位置為，（當前索引 + m） % 前面一輪元素個數。

那么根據這個公式，用代碼進行實現。

class Solution:def lastRemaining(self, n: int, m: int) -> int:ans = 0# 最后 1 位為最終保留數字# 往前逆推，從元素個數為 2 開始for i in range(2, n + 1):# 逆推公式ans = (ans + m) % ireturn ans

測試

import org.junit.Assert;
import org.junit.Test;public class LastRemainingTest {@Testpublic void test() {LastRemaining lr = new LastRemaining();Assert.assertEquals(3, lr.lastRemaining(5, 3));Assert.assertEquals(2, lr.lastRemaining(10, 17));Assert.assertEquals(3, lr.lastRemaining2(5, 3));Assert.assertEquals(2, lr.lastRemaining2(10, 17));}}

參考

1. LeetCode 面試題62. 圓圈中最后剩下的數字

2. LaTex數學公式生成