概述

1. （確定狀態）確定問題狀態
   • 提煉最后一步
   • 子問題轉化
2. （求得方程）轉移方程，把問題方程化
3. （設初置界）按照實際邏輯設置初始條件和邊界情況
4. （確序再解）確定計算順序并求解

一個案例：最少硬幣組合

你打算買一本27元的書，你現有三種硬幣，分別面值2元，5元和7元，每種硬幣都充足。請問如何用個數最少的硬幣組合正好付清？

正常人第一反應思路:

最少硬幣組合?

• 優先使用大面值硬幣 —— 7+7+7+5=26，不符合求解目標27元。
• 換種組合 —— 7+7+7+2+2+2=27，總共用了6枚硬幣正好27元。
• 實際正確答案 —— 7+5+5+5+5=27，才用了5枚硬幣。

所以這里貪心算法是并不適用。

題目中關鍵詞“最少的”，這是用到“動態規劃”的味道。

解決動態規劃問題4步

第一步，確定問題狀態

動態規劃問題求解需要先開一個數組，并確定數組的每個元素f[i]代表什么，這就是確定這個問題的狀態。這類似于解數學題中，設定x，y，z代表什么。

A、確定狀態首先提取“最后一步”

最優策略必定是K枚硬幣a1, a2, …, aK面值加起來是27。

找出不影響最優策略的最后一個獨立角色，這道問題中，那枚最后的硬幣aK就是最后一步。把aK提取出來，硬幣aK之前的所有硬幣面值加總是27-aK。因為總體求最硬幣數量最少策略，所以拼出27-aK的硬幣數也一定最少（重要設定）。

B、轉化子問題

最后一步aK提出來之后，我們只要求出“最少用多少枚硬幣可以拼出27- aK”就可以了。

這種與原問題內核一致，但是規模變小的問題，叫做子問題。

為簡化定義，我們設狀態f(X)=最少用多少枚硬幣拼出總面值X。

我們目前還不知道最后的硬幣aK面額多少，但它的面額一定只可能是{2, 5, 7}之一。

• 如果aK是2，f(27)應該是f(27-2) + 1(加上最后這一枚面值2的硬幣）
• 如果aK是5，f(27)應該是f(27-5) + 1(加上最后這一枚面值5的硬幣）
• 如果aK是7，f(27)應該是f(27-7) + 1(加上最后這一枚面值7的硬幣）

除此以外，沒有其他的可能了。至此，通過找到原問題最后一步，并將其轉化為子問題。

為求面值總額27的最小的硬幣組合數的狀態就形成了，用以下函數表示：

f(27) = min{f(27-2)+1, f(27-5)+1, f(27-7)+1}

第二步，轉移方程，把問題方程化

f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}

動態規劃都是要開數組，所以上面式子改用方括號表示。實際求解動態規劃類問題，正確列出轉移方程正確基本上就解決一半了。

遞歸的解法：

// f(X)返回最少用多少枚硬幣拼出X
int f(int X) {// 0元錢只要0枚硬幣if (X == 0) return 0;// 初始化用無窮大（int res = Integer.MAX_VALUE;// 最后一枚硬幣是2元if (X >= 2) {res = Math.min(f(X – 2) + 1, res);}// 最后一枚硬幣是5元if (X >= 5) {res =  Math.min(f(X – 5) + 1, res);}// 最后一枚硬幣是7元if (X >= 7) {      res =  Math.min(f(X – 7) + 1, res);}return res;
}

執行圖如下：

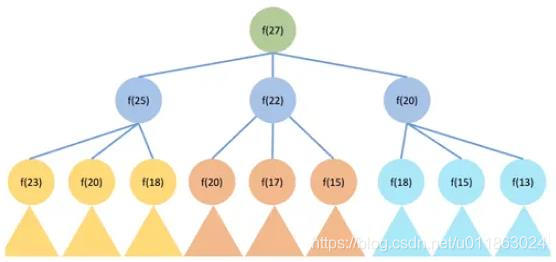
要算f(27)，就要遞歸f(25)、f(22)、f(20)，然后下邊依次遞歸。

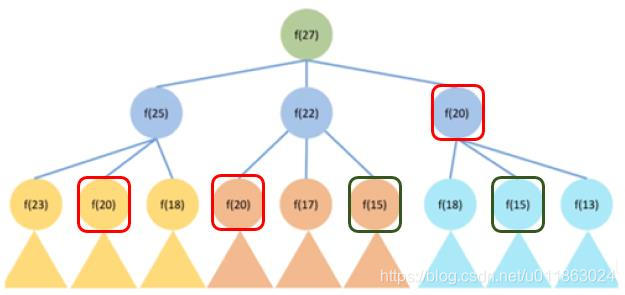
問題明顯：重復遞歸太多。

這是求f(27)，等待時間還可以接受。如果求f(100)呢？

求總體最值，可優先考慮動態規劃，不要貿然去遞歸。

第三步，按照實際邏輯設置邊界情況和初始條件。

如果不按照實際邏輯設置邊界情況和初始條件，即使轉移方程正確也大概率無法跑通代碼。

f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}的邊界情況是[x-2]、[x-5]、[x-7]不能小于0（硬幣面值為正），也不能高于27。

故對邊界情況設定如下：

如果硬幣面值不能組合出Y，就定義f[Y]=正無窮。例如，f[-1] = f[-2] = … = 正無窮，f[1] = min{f[-1]+1, f[-4]+1,f[-6]+1} = 正無窮，特殊情況：本題的F[0]對應的情況為F[-2]、F[-5]、F[-7]，按照上文的邊界情況設定結果是正無窮，但是實際上F[0]的結果是存在的（即使用0個硬幣的情況下），F[0]=0。

可是按照我們剛剛的設定，F[0]=F[0-2]+1= F[-2]+1=正無窮。豈不是矛盾？這種用轉移方程無法計算，但是又實際存在的情況，就必須通過手動定義。這里手動強制定義初始條件為：F[0]=0。

而從0之后的數值是沒矛盾的，比如F[1]= F[1-2]+1= F[-1]+1=正無窮（正無窮加任何數結果還是正無窮），F[2] = F[2-2]+1 = F[0]+1=1。

第四步，確定計算順序并計算求解

那么開始計算時，是從F[1]、F[2]開始呢？還是從F[27]、F[26]開始呢？

判斷計算順序正確與否的原則是：當我們要計算F[X]（等式左邊，如F[10]）的時候，等式右邊（f[X-2]，f[X-5]，f[X-7]等）都是已經得到結果的狀態，這個計算順序就是OK的。

實際就是從小到大的計算方式（偶有例外的情況）。

例如我們算到F[12]的時候，發現F[11]、F[10]、F[9]都已經算過了，這種算法就是對的。而開始算F[27]的時候，發現F[26]還沒有算，這樣的順序就是錯的。

很顯然這樣的情況下寫一個for循環就夠了。

回到這道題，采用動態規劃的算法，每一步只嘗試三種硬幣，一共進行了27步。算法時間復雜度（即需要進行的步數）為27*3。

與遞歸相比，沒有任何重復計算。

本文的題目來源：LeetCode - Medium - 322. Coin Change

代碼如下：

public class CoinChange {public int coinChange(int[] coins, int amount) {int[] f = new int[amount + 1];Arrays.fill(f, Integer.MAX_VALUE);f[0] = 0;for (int i = 1; i <= amount; i++) {//如果通過放這個硬幣能夠達到數量ifor(int coin : coins) {if (i >= coin && f[i - coin] != Integer.MAX_VALUE)// 獲得i的數量的硬幣數就可能是獲得i-A[j]重量硬幣數的方案+1// 拿這個方案數量與原本的方案數打擂臺，取最小值就行f[i] = Math.min(f[i - coin] + 1, f[i]);}}if (f[amount] == Integer.MAX_VALUE) {return -1;}return f[amount];}
}

總結

1. 這是求最值問題，用動態規劃方式求解。（案例：最少硬幣組合）
2. 進入求解過程，先確定問題狀態
   • 提煉最后一步（最優策略中使用的最后一枚硬幣aK）
   • 子問題轉化（最少的硬幣拼出更小的面值X-aK）
3. 構建轉移方程（f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}）
4. 設置初始條件和邊界情況（f[0] = 0, 如果不能拼出Y，f[Y]=正無窮）
5. 確定計算順序并計算求解（f[0], f[1], f[2],…）