二叉搜索樹

二叉查找樹（Binary Search Tree），（又：二叉搜索樹，二叉排序樹）它或者是一棵空樹，或者是具有下列性質的二叉樹：若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值；若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值；它的左、右子樹也分別為二叉排序樹。
具體介紹和實現：https://blog.csdn.net/hebtu666/article/details/81741034

我們知道，對于一般的二叉搜索樹（Binary Search Tree），其期望高度（即為一棵平衡樹時）為log2n，其各操作的時間復雜度（O(log2n)）同時也由此而決定。但是，在某些極端的情況下（如在插入的序列是有序的時），二叉搜索樹將退化成近似鏈或鏈，

此時，其操作的時間復雜度將退化成線性的，即O(n)。我們可以通過隨機化建立二叉搜索樹來盡量的避免這種情況，但是在進行了多次的操作之后，由于在刪除時，我們總是選擇將待刪除節點的后繼代替它本身，這樣就會造成總是右邊的節點數目減少，以至于樹向左偏沉。這同時也會造成樹的平衡性受到破壞，提高它的操作的時間復雜度。

概念引入

Abstract Self-Balancing Binary Search Tree：自平衡二叉搜索樹

顧名思義：它在面對任意節點插入和刪除時自動保持其高度

常用算法有紅黑樹、AVL、Treap、伸展樹、SB樹等。在平衡二叉搜索樹中，我們可以看到，其高度一般都良好地維持在O（log（n）），大大降低了操作的時間復雜度。這些結構為可變有序列表提供了有效的實現，并且可以用于其他抽象數據結構，例如關聯數組，優先級隊列和集合。

對于這些結構，他們都有自己的平衡性，比如：

AVL樹

具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉樹。

根據定義可知，這是根據深度最嚴苛的標準了，左右子樹高度不能差的超過1.

具體介紹和實現：https://blog.csdn.net/hebtu666/article/details/85047648

紅黑樹

特性:
（1）每個節點或者是黑色，或者是紅色。
（2）根節點是黑色。
（3）每個葉子節點（NIL）是黑色。?[注意：這里葉子節點，是指為空(NIL或NULL)的葉子節點！]
（4）如果一個節點是紅色的，則它的子節點必須是黑色的。
（5）從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。

根據定義，確保沒有一條路徑會比其他路徑長出2倍。

size balance tree

Size Balanced Tree（簡稱SBT）是一自平衡二叉查找樹，是在計算機科學中用到的一種數據結構。它是由中國廣東中山紀念中學的陳啟峰發明的。陳啟峰于2006年底完成論文《Size Balanced Tree》，并在2007年的全國青少年信息學奧林匹克競賽冬令營中發表。由于SBT的拼寫很容易找到中文諧音，它常被中國的信息學競賽選手和ACM/ICPC選手們戲稱為“傻B樹”、“Super BT”等。相比紅黑樹、AVL樹等自平衡二叉查找樹，SBT更易于實現。據陳啟峰在論文中稱，SBT是“目前為止速度最快的高級二叉搜索樹”。SBT能在O(log n)的時間內完成所有二叉搜索樹（BST）的相關操作，而與普通二叉搜索樹相比，SBT僅僅加入了簡潔的核心操作Maintain。由于SBT賴以保持平衡的是size域而不是其他“無用”的域，它可以很方便地實現動態順序統計中的select和rank操作。

對于SBT的每一個結點 t,有如下性質：
???性質(a) s[ right[t] ]≥s[ left [ left[ t ] ] ], s[ right [ left[t] ] ]
???性質(b) s[ left[t] ]≥s[right[ right[t] ] ], s[ left[ right[t] ] ]
即.每棵子樹的大小不小于其兄弟的子樹大小。

伸展樹

伸展樹（Splay Tree）是一種二叉排序樹，它能在O(log n)內完成插入、查找和刪除操作。它由Daniel Sleator和Robert Tarjan創造。它的優勢在于不需要記錄用于平衡樹的冗余信息。在伸展樹上的一般操作都基于伸展操作。

Treap

Treap是一棵二叉排序樹，它的左子樹和右子樹分別是一個Treap，和一般的二叉排序樹不同的是，Treap紀錄一個額外的數據，就是優先級。Treap在以關鍵碼構成二叉排序樹的同時，還滿足堆的性質(在這里我們假設節點的優先級大于該節點的孩子的優先級)。但是這里要注意的是Treap和二叉堆有一點不同，就是二叉堆必須是完全二叉樹，而Treap并不一定是。

對比可以發現，AVL樹對平衡性的要求比較嚴苛，每插入一個節點就很大概率面臨調整。

而紅黑樹對平衡性的要求沒有那么嚴苛。可能是多次插入攢夠了一下調整。。。

把每一個樹的細節都扣清楚是一件挺無聊的事。。雖然據說紅黑樹都成了面試必問內容，但是實在是不想深究那些細節，這些樹的基本操作也無非是那么兩種：左旋，右旋。這些樹的所有操作和情況，都是這兩種動作的組合罷了。

所以本文先介紹這兩種基本操作，等以后有時間（可能到找工作時），再把紅黑樹等結構的細節補上。

最簡單的旋轉

最簡單的例子：

這棵樹，左子樹深度為2，右子樹深度為0，所以，根據AVL樹或者紅黑樹的標準，它都不平衡。。

那怎么辦？轉過來：

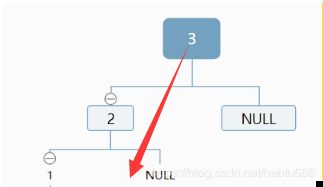
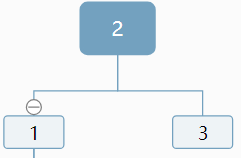
是不是就平衡了？

這就是我們的順時針旋轉，又叫，右旋，因為是以2為軸，把1轉下來了。

左旋同理。

帶子樹旋轉

問題是，真正轉起來可沒有這么簡單：

這才是一顆搜索樹的樣子啊

ABCD都代表是一顆子樹。我們這三個點轉了可不能不管這些子樹啊對不對。

好，我們想想這些子樹怎么辦。

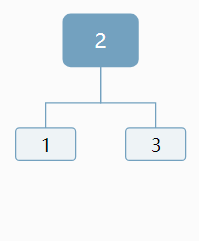
首先，AB子樹沒有關系，放在原地即可。

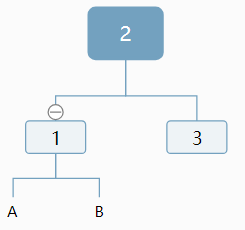
D作為3的右子樹，也可以不動，那剩下一個位置，會不會就是放C子樹呢？

我們想想能否這樣做。

原來：

1）C作為2的右子樹，內任何元素都比2大。

2）C作為3左子樹的一部分，內任何元素都比3小。

轉之后：

1）C作為2的右子樹的一部分，內任何元素都比2大。

2）C作為3左子樹，內任何元素都比3小。

所以，C子樹可以作為3的左子樹，沒有問題。

這樣，我們的操作就介紹完了。

這種基本的變換達到了看似把樹變的平衡的效果。

左右旋轉類似

代碼實現

對于Abstract BinarySearchTree類，上面網址已經給出了思路和c++代碼實現，把java再貼出來也挺無趣的，所以希望大家能自己實現。

抽象自平衡二叉搜索樹（AbstractSelfBalancingBinarySearchTree）的所有操作都是建立在二叉搜索樹（BinarySearchTree?）操作的基礎上來進行的。

各種自平衡二叉搜索樹（AVL、紅黑樹等）的操作也是由Abstract自平衡二叉搜索樹的基本操作：左旋、右旋構成。這個文章只寫了左旋右旋基本操作，供以后各種selfBalancingBinarySearchTree使用。

public abstract class AbstractSelfBalancingBinarySearchTree extends AbstractBinarySearchTree {protected Node rotateRight(Node node) {Node temp = node.left;//節點2temp.parent = node.parent;//節點3的父(旋轉后節點2的父)node.left = temp.right;//節點3接收節點2的右子樹if (node.left != null) {node.left.parent = node;}temp.right = node;//節點3變為節點2的右孩子node.parent = temp;//原來節點3的父（若存在），孩子變為節點2if (temp.parent != null) {if (node == temp.parent.left) {temp.parent.left = temp;} else {temp.parent.right = temp;}} else {root = temp;}return temp;}protected Node rotateLeft(Node node) {Node temp = node.right;temp.parent = node.parent;node.right = temp.left;if (node.right != null) {node.right.parent = node;}temp.left = node;node.parent = temp;if (temp.parent != null) {if (node == temp.parent.left) {temp.parent.left = temp;} else {temp.parent.right = temp;}} else {root = temp;}return temp;}
}