動態規劃 Dynamic Programming DP
?
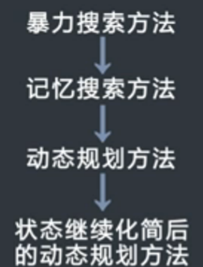
準則
動態規劃的本質，是對問題狀態的定義和狀態轉移方程的定義。
動態規劃是通過拆分問題，定義問題狀態和狀態之間的關系，使得問題能夠以遞推（或者說分治）的方式去解決。
如何拆分問題，才是動態規劃的核心。
而拆分問題，靠的就是狀態的定義和狀態轉移方程的定義。
?
以LIS為例，重新定義這個問題：
給定一個數列，長度為N，
設F_{k}為：以數列中第k項結尾的最長上升子序列的長度.
求F_{1}..F_{N} 中的最大值.
對于F_{k}來講，F_{1} .. F_{k-1}都是F_{k}的子問題：因為以第k項結尾的最長遞增子序列（下稱LIS），包含著以第1..k-1中某項結尾的LIS。
?
上述的新問題F_{k}也可以叫做狀態，定義中的“F_{k}為數列中第k項結尾的LIS的長度”，就叫做對狀態的定義。
之所以把F_{k}做“狀態”而不是“問題” ，一是因為避免跟原問題中“問題”混淆，二是因為這個新問題是數學化定義的。
?
上述狀態定義好之后，狀態和狀態之間的關系式，就叫做狀態轉移方程。
比如，對于LIS問題，狀態轉移方程為：
以第k項結尾的LIS的長度是：保證第i項比第k項小的情況下，以第i項結尾的LIS長度加一的最大值，取遍i的所有值（i小于k）。
?
a. “緩存”，“重疊子問題”，“記憶化”
這三個名詞，都是在闡述遞推式求解的技巧。以Fibonacci數列為例，計算第100項的時候，需要計算第99項和98項；在計算第101項的時候，需要第100項和第99項，這時候你還需要重新計算第99項嗎？不需要，你只需要在第一次計算的時候把它記下來就可以了。上述的需要再次計算的“第99項”，就叫“重疊子問題”。如果沒有計算過，就按照遞推式計算，如果計算過，直接使用，就像“緩存”一樣，這種方法，叫做“記憶化”，這是遞推式求解的技巧。這種技巧，通俗的說叫“花費空間來節省時間”。都不是動態規劃的本質，不是動態規劃的核心。
b. “自上而下”，“自下而上”
“遞歸”：遞歸是遞推式求解的方法，連技巧都算不上。
怎么實現dp？答：兩種常用的方法。（僅僅涉及一般問題）?????
?1. 自下而上：通過正向的loop，求出所有狀態對應的值，然后找出max或者min。???????????? 優缺點：速度慢，但是相對節省空間。?????
2. 自上而下：通過遞歸的方法，需要求解f(x)，則必須知道f(y)，要知道f(y)，必須求f(z).??????????? 優缺點：速度快，只用算需要的值，但是要調用堆棧，浪費空間。
?
c. "無后效性"，“最優子結構”
上述的狀態轉移方程中，等式右邊不會用到下標大于左邊i或者k的值，這是"無后效性"的通俗上的數學定義，符合這種定義的狀態定義，我們可以說它具有“最優子結構”的性質，在動態規劃中我們要做的，就是找到這種“最優子結構”。
每個階段的最優狀態可以從之前某個階段的某個或某些狀態直接得到
這個性質叫做最優子結構；
而不管之前這個狀態是如何得到的
這個性質叫做無后效性。
在對狀態和狀態轉移方程的定義過程中，滿足“最優子結構”是一個隱含的條件（否則根本定義不出來）。
d. 關于復雜度的分析
時間復雜度O （狀態數 * 每個狀態下所對應的決策數）。
空間復雜度O （狀態數）。
 深入淺出TCPIP之TCP套接字參數)
深入淺出TCPIP之Hello CDN)
)