序言
1對1的線性結構，一對多的樹二叉樹以及森林，第3種就是多對多的結構，也就是我們所要講到的圖的結構，圖形結構是數據結構當中最復雜的一種結構，圖形結構的特點就是在這個圖當中任意兩點之間都會有關系，這里的關系指的是可能會有關系，因為不是一對多也不是1對1，所以沒有辦法區分層次和順序了，圖上的頂點與頂點之間，我們可以認作是平等的，那我們如何去描述圖形結構？
在這里我們會提到兩個概念，一個是頂點集，一個是弧集，在這里要區分弧跟邊兒的概念，
對于前面1對1和一對多的關系，我們是可以用數據來進行描述它們之間的關系的，也很方便找到他們的前驅和后繼，1對1或者是一對多的關系，他們之間的數據與數據之間都有一定的關系，找到某一個數據之后，另外的數據就可以根據前一個數據進行推導出來，和我們現在所提到的圖的結構是有區別的，圖的結構在描述數據與數據之間的關系時，所采用的描述方式包括了邊兒，邊兒的方向決定了數據與數據之間存在怎樣的關系，那為什么說描述不了圖形之間的關系？因為圖形當中點和點之間的關系是不確定的，他們沒有一個確定的關系，并不像樹形結構一樣，可以看作是一個家族家族之間存在血緣關系，但是對于圖來說點和點之間是沒有血緣關系的，
【1】根據圖形結構，我們能夠想到哪些個東西？
圖形結構就是把沒有關系的點和點之間通過一些個輔助條件轉化成為一種有關系的結構，只有當輔助條件相當多的時候，我們才能夠描述出圖形之間點和點之間各種數據關系
【2】圖的概念？
圖是有一個頂點及V和一個弧集R構成的數據結構
弧描述了點與點之間的關系，是一條有效線段，起點為弧尾，終點為弧頭
有向圖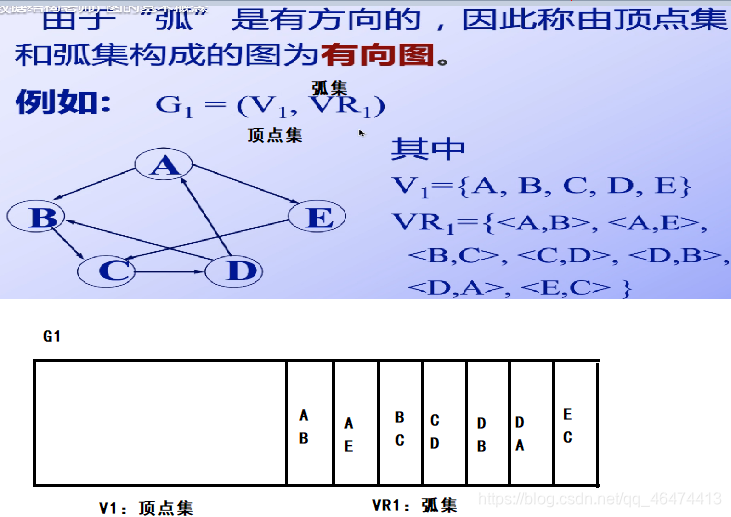
此時a和b之間的關系是不相等的，是對于有象圖來說的，因為有象圖包含弧，也就是包含一條有向線段
無向圖
先提出的弧的概念，有弧推廣得到的邊的概念，若一根弧正向屬于弧，反過來也屬于弧，那么我們就概括為邊的概念
【1】相等：如果兩個點之間存在邊，那么我們就認為這兩個點之間的關系是平級的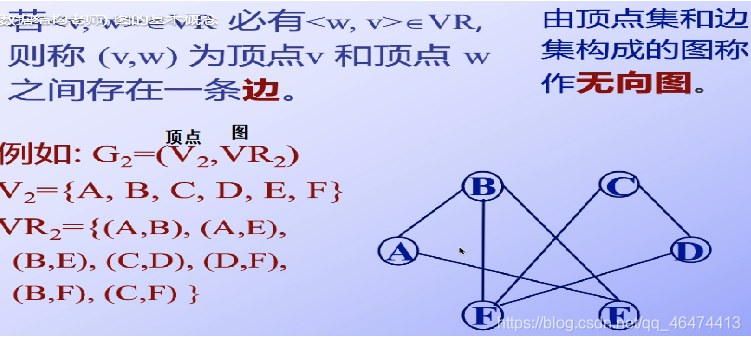
相關術語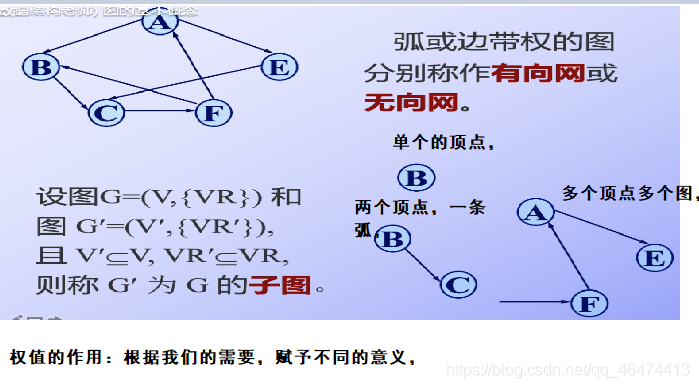
nlogn是我們人為規定的，我們根據需要來進行規定，拿些我們可以認為是稀疏圖，哪些我們認為是稠密的圖都是我們自己決定的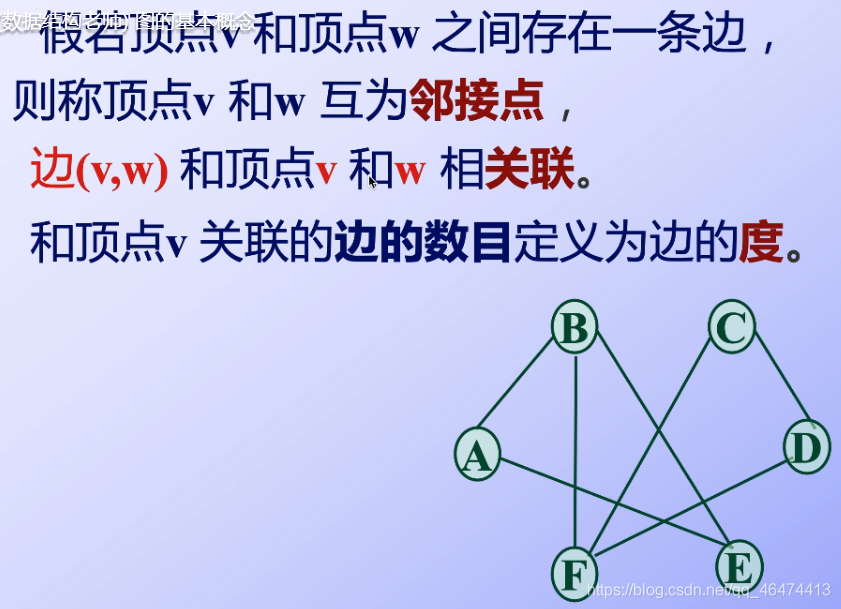
我們注意：關聯是三者之間的一種關系，而不是點與點之間的一種關系，要包括他們之間的邊
我們在講哈弗曼樹的時候提到過路徑的概念，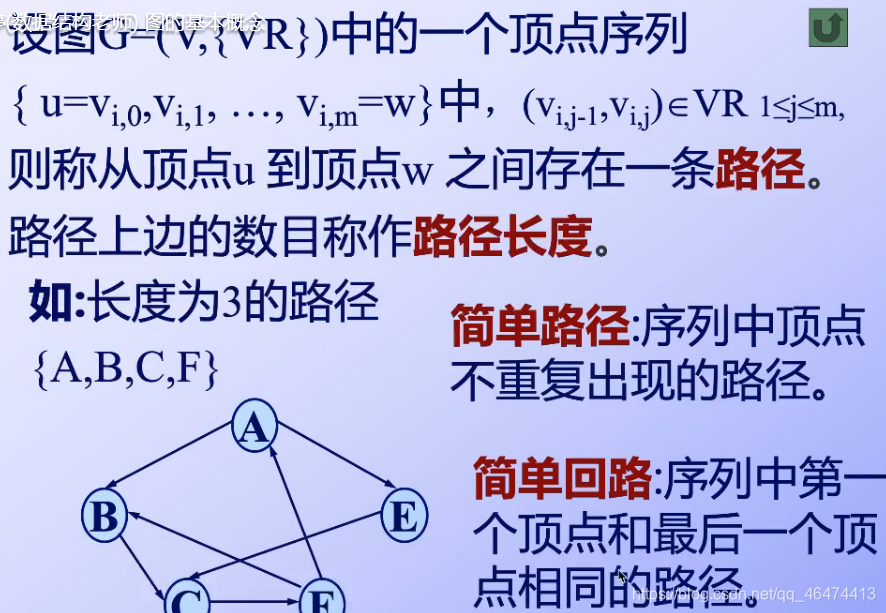
簡單回路是由簡單路徑組成的，不能出現重復的點----簡單回路是在簡單路徑中提出來的，具有基礎性質
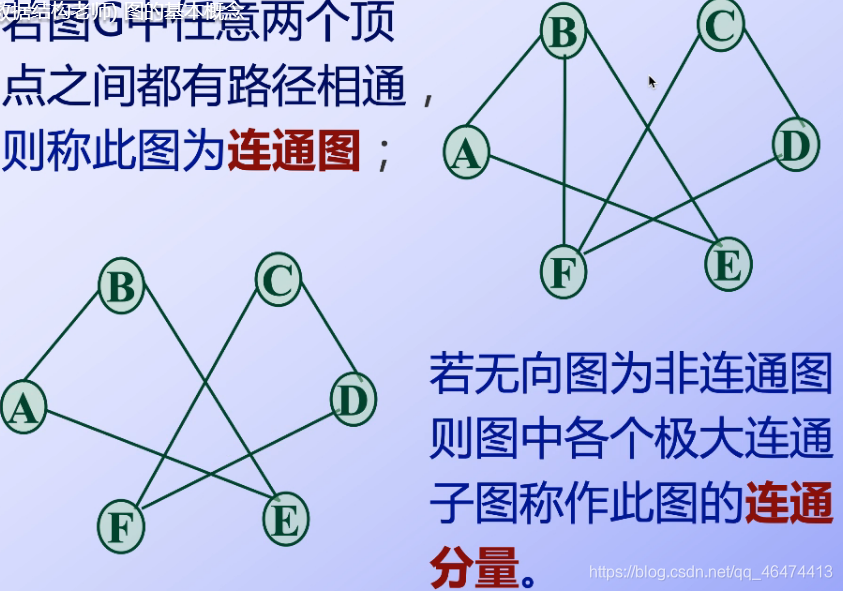判斷聯通圖的方法？
點與點之間是有一條或多條邊連接在一起的，不能夠單獨拆開，如果拆開了，那就是聯通分量
對于有向圖來說，若任意兩個頂點之間都存在一條有向路徑，那么稱此有向圖為強連通圖簡單的來說就是有出度和入度
圖的生成樹
先說一種思想：
復雜的東西我們要往簡單的方向考慮，這樣我們的編碼生活才會更加的簡單-----復雜的東西簡單化但是我們解決復雜的東西我們要找到對應的關系，就像是我們想要馬拉松比賽，那么我們可以找到每一段對應的終點，將復雜的問題簡單化
生成樹是什么？
首先我們要知道生成樹是原圖的一個子圖，此圖的特性是包含原圖的所有頂點，以及其中的n-1條邊，這n-1條邊是從原來的一條邊開始進行尋找，通過n-1條邊能夠將原來的所有頂點連接到一起，形成一個連通子圖，所謂的聯通就是沒有孤立的點
問題：用到哪些特性了？
如果我們將n個頂點用n-1條邊連接起來，要把它作為聯通的圖，就一定不會出現回路，基本可以肯定的是他是一個樹形結構，不會存在圈兒，到每一個點有唯一一條線與它連接，因此引出了樹形結構，我們的樹形結構從下向上看，除了根節點，每一個頂點都有唯一一個指針指向他，我們試想一下，我們有5個點，如果我們用4條邊將5個點連接在一起，那么就不會出現回路的情況，三角形是有三個頂點，三條邊，正方形是有4個頂點，4條邊，當邊與頂點的數值相同的時候才會出現回路，
聯通圖才可以得到生成樹，
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
圖的存儲表示
我們知道存儲結構有兩大類，一類是順序結構，一類是鏈式結構，但是對于簡單的順序結構以及鏈式結構是不能夠滿足圖的存儲使用的，需要在此基礎上做出一些改變，
圖的鄰接矩陣表示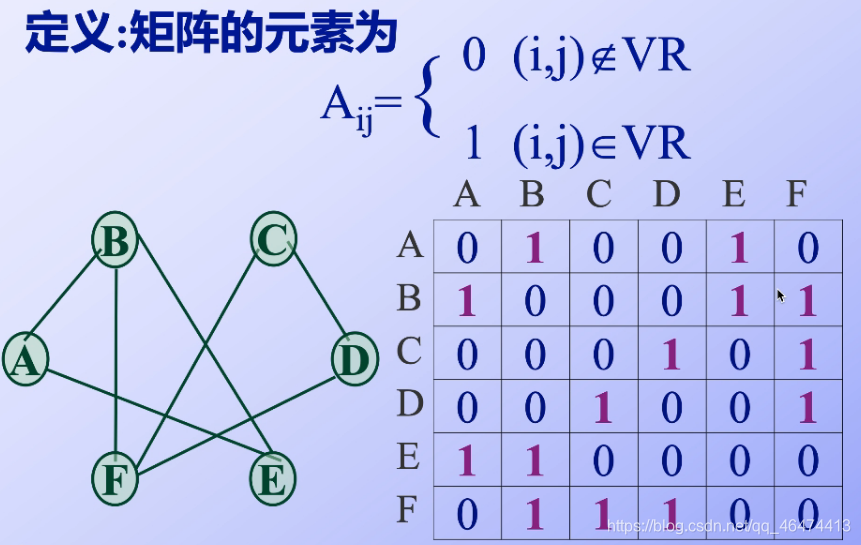
總結以下特點：
【1】：對于無向圖來說，鄰接矩陣就是對稱的，因為我們的線段是從兩個方向同時指出來的，那么我們就需要記錄兩個1，因此我們應該想到的是前面提到的三角矩陣
計算
有向圖的鄰接矩陣不一定是對稱矩陣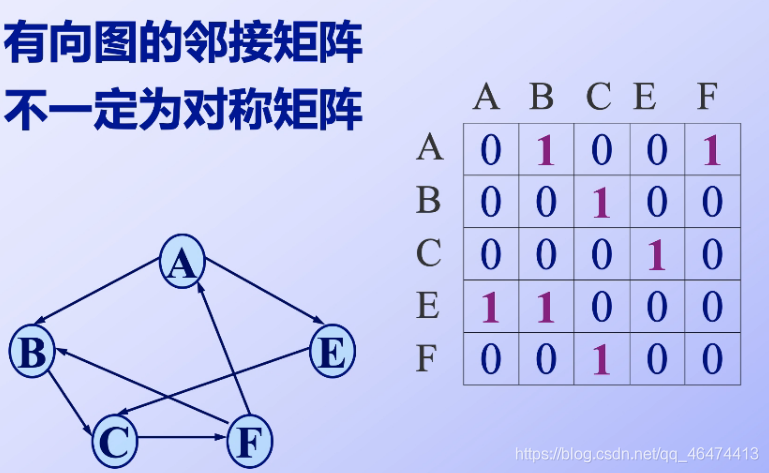
我們如何計算頂點的出度以及入度？
首先我們應該找到節點所在的行，行上面的1代表的就是出度，列代表的是入度，總的度我們用出度加上入度來進行表示就可以了
圖上的矩陣數據表示的是邊或者弧，而不是表示的節點問題，因此我們在進行結點的刪除以及添加的時候，我們還是不方便的，原因是我們使用的是線性結構，而不是鏈式結構，因此下面我們將要介紹的就是鏈式結構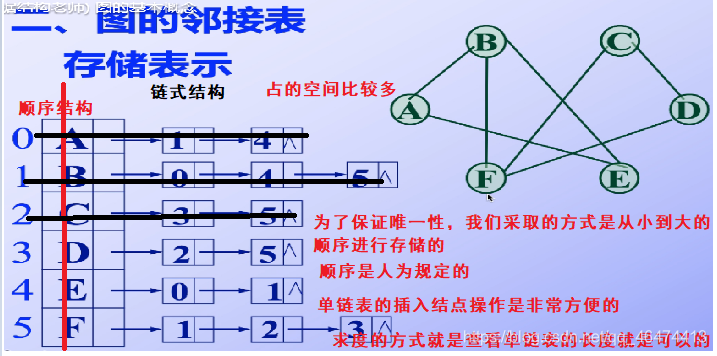
有向圖是分為兩種的，一種是正向的，后面的連接是從小到大的，另外一種是反向的，對應的鏈接表時從大到小進行連接的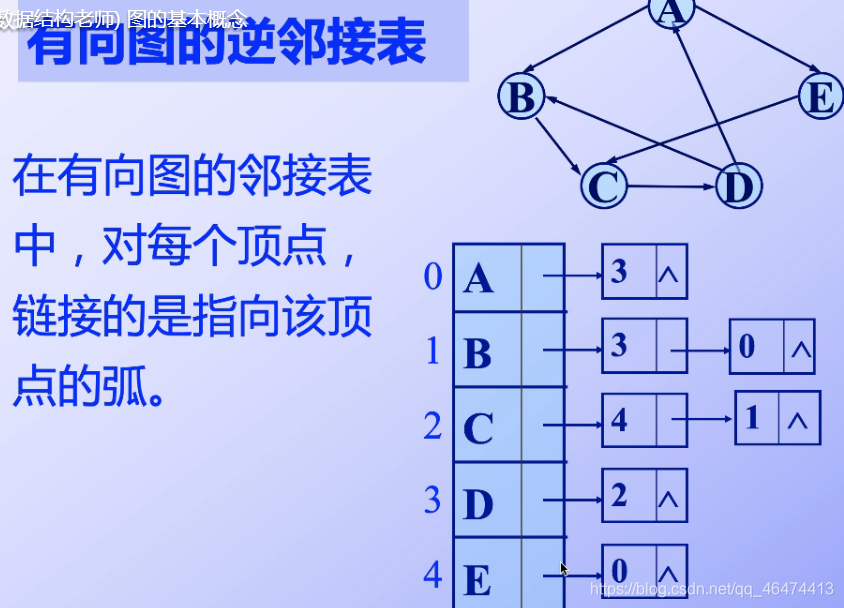
)
