一.文章概述

本文提出了一種自監督屬性圖生成任務來預訓練GNN，使得其能捕圖的結構和語義屬性。作者將圖的生成分為兩個部分：屬性生成和邊生成，即給定觀測到的邊，生成節點屬性；給定觀測到的邊和生成的節點屬性，生成剩余的邊。通過這種方式使得模型能捕獲每個節點屬性和結構之間的依賴關系。對于每個節點，GPT-GNN可以同時計算其屬性生成和邊生成損失。另外，為了使得GPT-GNN可以處理大圖，作者采用了子圖采樣技術，并提出自適應嵌入隊列來緩解負采樣帶來的不準確損失。

二.預備知識

之前關于圖上預訓練的工作可以分為兩類：

• network/graph embedding：直接參數化節點嵌入向量，并通過保留一些相似度量來參數化的優化節點嵌入。但該種方式學到的嵌入不能用于初始化其他模型，以便對其他任務進行微調。
• transfer learning setting：預訓練一個可用于處理不同任務的通用GNN。

三.GNN的生成式預訓練

3.1 GNN預訓練問題

為什么需要預訓練？

獲取足夠的標注數據通常具有挑戰性，尤其是對于大圖，這阻礙了通用GNN的訓練。為此，有必要探索GNN的預訓練，它能用很少的標簽進行泛化。

GNN預訓練的正式定義：GNN預訓練的目標是完全基于單個（大規模）圖$G=(\mathcal{V},\mathcal{E},\mathcal{X})$ 學習一個通用的GNN模型$f_{\theta }$，而不需要標注數據，這使得$f_{\theta }$對于同一個圖或同一領域的圖上的各種下游任務是一個良好的初始化。

3.2 生成式預訓練框架

作者提出GPT-GNN，它通過重建/生成輸入圖的結構或屬性來預訓練GNN。

給定輸入圖$G=(\mathcal{V},\mathcal{E},\mathcal{X})$，GNN模型$f_{\theta }$，作者用GNN$f_{\theta }$建模圖上的似然（likelihood）為$p(G;\theta )$，其表示圖$G$中的節點是如何歸屬（attributed）和連接（connected）的。GPT-GNN旨在預訓練GNN來最大化圖似然，即${\theta }^{?}={\text{max}}_{\theta }p(G;\theta )$。

3.2.1 如何建模$p(G;\theta )$

現有的大多數圖生成方式采用自回歸的方式對概率目標進行因式分解，即按圖中的節點順序來，通過將每個新到達的節點連接到現有節點來生成邊。類似地，作者用排列（permutation）向量$\pi$來確定節點順序，其中$i^{\pi }$表示排列$\pi$中第$i$個位置的節點id。因此，圖分布$p(G,\theta )$等價于所有可能排列的期望的可能性，即：
$$p(G;\theta )={\mathbb{E}}_{\pi }\left[p_{\theta }\left(X^{\pi },E^{\pi }\right)\right],$$
其中$X^{\pi }\in \mathbb{R}|\mathcal{V}|\times d$表示排列的節點屬性，$E$是邊集，$E_i^{\pi }$表示與$i^{\pi }$相連的所有邊。為了簡化，作者假設觀察任何節點排列$\pi$的概率相同。給定一個排列順序，可以自回歸分解log四讓，每次迭代生成一個節點：
$$\log p_{\theta }(X,E)=\sum _{i=1}^{|\mathcal{V}|}\log p_{\theta }\left(X_i,E_i\mid X_{<i},E_{<i}\right)$$
在每一步$i$，作者使用$i$之前的所有生成的節點，以及其對應的屬性$X_{<i}$、節點間的結構$E_{<i}$來生成新的節點$i$，包括$i$的屬性$X_i$和與已有節點的連接$E_i$。

3.3 分解屬性圖生成

對于條件概率 $p_{\theta }\left(X_i,E_i\mid X_{<i},E_{<i}\right)$ 的建模，一個簡單的解決方案是假設$X_i$和$E_i$是獨立的，即：
$$p_{\theta }\left(X_i,E_i\mid X_{<i},E_{<i}\right)=p_{\theta }\left(X_i\mid X_{<i},E_{<i}\right)?p_{\theta }\left(E_i\mid X_{<i},E_{<i}\right)$$
采用該種方式時，對每個節點其屬性和連接之間的依賴關系被完全忽略了，但這種忽略的依賴性確是屬性圖的核心屬性，也是GNN中卷積聚合的基礎，因此，這種樸素的分解不能為預訓練GNN提供指導。

為了解決這一問題，作者提出了依賴感知（dependency-aware）分解機制來進行屬性圖的生成。具體來說，在估計一個新節點的屬性時，其結構信息會被給定，反之亦然，即屬性圖的生成可以分為兩步：

• 給定觀測到的邊，生成節點屬性；
• 給定觀察到的邊和生成的節點屬性，生成剩余的邊。

通過這種方式，模型可以捕獲每個節點的屬性和結構之間的依賴關系。

令$o$表示$E_i$中所有觀察到的邊的索引向量，則$E_{i,o}$表示觀測到的邊。$?o$表示所有掩去邊的索引，即待生成的邊。基于此，條件概率可以重寫為所有觀察到的邊的期望可能性：
$$\begin{array}{rl}& p_{\theta }\left(X_i,E_i\mid X_{<i},E_{<i}\right)\\ =& \sum _o{p}_{\theta }\left(X_i,E_{i,?o}\mid E_{i,o},X_{<i},E_{<i}\right)?p_{\theta }\left(E_{i,o}\mid X_{<i},E_{<i}\right)\\ =& {\mathbb{E}}_o\left[p_{\theta }\left(X_i,E_{i,?o}\mid E_{i,o},X_{<i},E_{<i}\right)\right]\\ =& {\mathbb{E}}_o[\underset{\text{1)?generate?attributes?}}{\underbrace{p_{\theta }\left(X_i\mid E_{i,o},X_{<i},E_{<i}\right)}}?\underset{\text{2)?generate?edges?}}{\underbrace{p_{\theta }\left(E_{i,?o}\mid E_{i,o},X_{\le i},E_{<i}\right)}}].\end{array}$$
其中$p_{\theta }\left(X_i\mid E_{i,o},X_{<i},E_{<i}\right)$表示節點$i$的屬性生成，基于觀測到的邊$E_{i,o}$，可以聚集目標節點$i$的鄰域信息來生成屬性$X_i$。$p_{\theta }\left(E_{i,?o}\mid E_{i,o},X_{\le i},E_{<i}\right)$表示生成掩去的邊，基于觀測到的邊 $E_{i,o}$和生成的屬性$X_i$，可以生成目標節點$i$的表示，然后預測$E_{i,?o}$內的每條邊是否存在。

3.4 高效的屬性和邊生成

作者希望同時進行屬性生成和邊生成，但邊的生成需要節點屬性作為輸入，可以泄露給屬性生成。為了避免信息泄露，作者將每個節點設計為兩種類型：

• Attribute Generation Nodes：作者將這些節點的屬性掩去，并使用dummy token代替它們的屬性，并學得一個共享的向量$X^{init}$來表示它。
• Edge Generation Nodes：對這些節點保持其屬性，并將其作為GNN的輸入。

作者使用$h^{Attr}$和 $h^{Edge}$來分別表示Attribute Generation和Edge Generation節點，由于Attribute Generation Nodes被掩去，$h^{\text{Attr?}}$比$h^{Edge}$包含更少的信息。因此，在進行GNN的消息傳遞的時候，僅使用Edge Generation Nodes的輸出$h^{Edge}$作為對外信息。然后，使用這兩組節點的表示來生成具有不同解碼器的屬性和邊。

對于屬性生成，將其對應解碼器表示為${\text{Dec}}^{Attr}(?)$，它以$h^{\text{Attr?}}$作為輸入，生成被掩去的屬性。建模的選擇取決于屬性的類型。例如如果一個節點的輸入屬性是文本，則使用文本生成器模型(例如，LSTM)來生成它。此外，作者定義距離函數來作為生成屬性和真實值間的度量，即屬性生成損失定義為：
$${\mathcal{L}}_i^{\text{Attr?}}=\text{?Distance?}\left({\text{?Dec?}}^{\text{Attr?}}\left(h_i^{\text{Attr?}}\right),X_i\right).$$
對于邊的生成，作者假設每條邊的生成都是獨立的，然后可以隱式分解似然：
$$p_{\theta }\left(E_{i,?o}\mid E_{i,o},X_{\le i},E_{<i}\right)=\prod _{j^{+}\in E_{i,?o}}{p}_{\theta }\left(j^{+}\mid E_{i,o},X_{\le i},E_{<i}\right).$$
在獲取到Edge Generation node表示$h^{Edge}$后，可以通過${\mathrm{Dec}}^{Edge}\left(h_i^{Edge},h_j^{Edge}\right)$來建模節點$i$與節點$j$連接的可能性，其中$De{c}^{Edge}$表示成對（pairwise）得分函數。最后，采用負對比估計（negative contrastive estimation）來計算每個鏈接節點$j^{+}$的似然。作者將為連接的節點表示為$S_i^{?}$，對比損失計算公式如下：
L i E d g e = ? ∑ j + ∈ E i , ? o log ? exp ? ( Dec ? E d g e ( h i E d g e , h j + E d g e ) ) ∑ j ∈ S i ? ∪ { j + } exp ? ( Dec ? E d g e ( h i E d g e , h j E d g e ) ) \mathcal{L}_i^{E d g e}=-\sum_{j^{+} \in E_{i, \neg o}} \log \frac{\exp \left(\operatorname{Dec}^{E d g e}\left(h_i^{E d g e}, h_{j^{+}}^{E d g e}\right)\right)}{\sum_{j \in S_i^{-} \cup\left\{j^{+}\right\}} \exp \left(\operatorname{Dec}^{E d g e}\left(h_i^{E d g e}, h_j^{E d g e}\right)\right)} LiEdge?=?j+∈Ei,?o?∑?log∑j∈Si??∪{j+}?exp(DecEdge(hiEdge?,hjEdge?))exp(DecEdge(hiEdge?,hj+Edge?))?
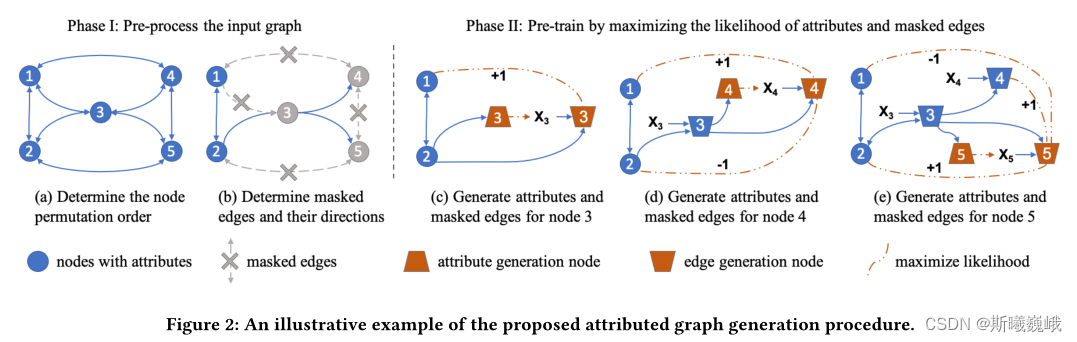
下圖便展示了屬性圖生成的過程：

• 確定輸入圖的節點排列順序；
• 隨機選取目標節點邊的一部分作為觀測邊$E_{i,o}$，剩下的邊掩去作為$E_{i,?o}$，需要將被掩去的邊從圖中刪除。
• 將節點劃分為Attribute Generation和Edge Generation節點。
• 使用修改的鄰接矩陣來計算節點3、4和5的表示，包括它們的Attribute和Edge Generation節點。
• 通過每個節點的屬性預測和掩去邊預測任務并行訓練GNN模型。

3.5 擴展到異配和大圖

本節主要介紹如何在大圖和異配圖上應用GPT-GNN進行預訓練。

異配圖：對于異配圖，所提出的GPT-GNN框架可以直接應用于預訓練異構GNN。唯一的區別是每種類型的節點和邊都可以有自己的解碼器，這是由異構gnn指定的，而不是預訓練框架。所有其他組件保持完全相同。

大圖：對于大圖，則需要使用子圖采樣進行訓練。為了估計GPT-GNN提出的對比損失，需要遍歷輸入圖的所有節點。然而，只能訪問子圖中的采樣節點來估計這個損失，使得(自)監督只關注局部信號。為了緩解這個問題，作者提出了自適應隊列（Adaptive Queue），它將之前采樣的子圖中的節點表示存儲為負樣本。每次處理一個新的子圖，可以通過添加最新的節點表示并刪除最舊的節點表示來逐步更新這個隊列。自適應隊列可以使用更大的負樣本池$S_i^{?}$，此外，不同采樣子圖上的節點可以為對比學習帶來全局結構指導。