什么是數學規劃？

數學建模中的數學規劃是指利用數學方法和技巧對問題進行數學建模，并通過數學規劃模型求解最優解的過程。數學規劃是一種數學優化方法，旨在找到使目標函數達到最大值或最小值的變量取值，同時滿足一系列約束條件。

數學規劃包括多種不同類型的問題，其中最常見的包括線性規劃（Linear Programming）、整數規劃（Integer Programming）、非線性規劃（Nonlinear Programming）、混合整數規劃（Mixed Integer Programming）等。

線性規劃在前面的回答中已經介紹過，它適用于目標函數和約束條件均為線性的情況。

整數規劃是線性規劃的擴展，其中決策變量被限制為整數取值。這種問題常見于在決策中需要選擇整數數量或整數類型的情況，如裝載問題、制定生產計劃等。

非線性規劃則涉及目標函數和/或約束條件含有非線性項的情況。此類問題的求解相對復雜，通常需要使用迭代和數值優化算法，如牛頓法、擬牛頓法等。

混合整數規劃結合了整數規劃和非線性規劃的特點，既包含整數變量，又涉及非線性項。這種問題在實際應用中廣泛存在，例如運輸路線優化、設備安排等。

數學規劃的求解方法包括傳統的數值優化算法（如單純形法、分支定界法）和近年來發展起來的啟發式算法（如遺傳算法、模擬退火算法）。通過結合不同的約束條件和求解算法，可以針對特定問題選擇最合適的數學規劃方法。

總之，數學規劃是數學建模中重要的工具，通過建立適當的數學模型，可以解決各種實際問題，并為決策提供科學依據。

數學規劃的一般形式：

數學規劃的一般形式可以表示為如下的數學模型：

最小化（或最大化）目標函數：

[ f(x) ]

在給定約束條件下，求解決策變量 ( x ) 的最優解。這里的決策變量可以是一個向量或者一組變量。

約束條件包括等式約束和不等式約束，可以表示為：

等式約束：

[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]

不等式約束：

[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]

其中， ( gi(x) ) 和 ( hj(x) ) 分別表示等式約束和不等式約束的函數，它們與決策變量 ( x ) 有關。

一般情況下，還需要給定決策變量 ( x ) 的取值范圍（上下界約束）：

[ x{\text{min}} \leq x \leq x{\text{max}} ]

最優解滿足所有約束條件，并且使目標函數取得最小（或最大）值。

數學規劃的具體形式會根據具體問題的特點而有所不同。常見的數學規劃模型包括線性規劃（LP）、整數規劃（IP）、非線性規劃（NLP）、混合整數規劃（MIP）等。

在數學規劃中，通常會使用數值優化算法來求解最優解，這些算法包括線性規劃的單純形法、內點法，以及非線性規劃的牛頓法、擬牛頓法等。近年來，啟發式算法如遺傳算法、粒子群優化等也在數學規劃中得到廣泛應用。

?

數學規劃的分類：

數學規劃可以根據問題的特性進行不同的分類。以下是常見的數學規劃分類：

1.線性規劃（Linear Programming, LP）：目標函數和約束條件均為線性的規劃問題。決策變量的取值可以是實數。線性規劃是最早和最經典的數學規劃問題之一。

2.整數規劃（Integer Programming, IP）：線性規劃的擴展，決策變量被限制為整數取值。這種問題常見于需要選擇整數數量或整數類型的場景，如裝載問題、制定生產計劃等。

3.非線性規劃（Nonlinear Programming, NLP）：目標函數和/或約束條件具有非線性項的規劃問題。這種問題的數學模型更復雜，通常需要使用迭代和數值優化算法來求解，如牛頓法、擬牛頓法等。

4.0-1規劃（0-1 Programming）：整數規劃的特列，整數變量的取值只能為0和1。

?

線性規劃問題的求解

1. matlab中線性規劃的標準型

?

1. matlab求解線性規劃的命令

函數linprog（）

接收值：

X：目標函數中x1，x2……xm的求解值

Fval：目標函數求取最小值的值

參數值：

C：目標函數的系數

A：不等式約束的系數

b：不等式約束的常數項

Aeq：等式約束的系數

Beq:等式約束的常數項

Lb：目標函數中自變量x1……xm的下限

Ub：目標函數中自變量x1……xm的上限

X0:初始值（在一些規劃中可以不添加）

?

線性規劃練習題：

在求解過程中需要將系數/常數的向量轉置成如下列例題中列好的列向量，方法在定義好的行向量后加’:[]’

規劃函數只能求最小值，若題目中有最大值或>=的不等式約束要在對應的式子中添加負號變為min/<=。其余式子不變。

?

參考代碼：

%% Matlab求解線性規劃% [x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)?% c是目標函數的系數向量，A是不等式約束Ax<=b的系數矩陣，b是不等式約束Ax<=b的常數項% Aeq是等式約束Aeq x=beq的系數矩陣，beq是等式約束Aeq x=beq的常數項% lb是X的下限，ub是X的上限，X是向量[x1,x2,...xn]' , 即決策變量。% 迭代的初始值為x0（一般不用給）% 更多該函數的用法說明請看講義%% 例題1c = [-5 -4 -6]';? % 加單引號表示轉置% c = [-5 -4 -6];? % 寫成行向量也是可以的，不過不推薦，我們按照標準型來寫看起來比較正規A = [1 -1 1;3 2 4;3 2 0];b = [20 42 30]';??lb = [0 0 0]';[x fval] = linprog(c, A, b, [], [], lb)? % ub我們直接不寫，則意味著沒有上界的約束% x =%????????? 0%??? 15.0000%???? 3.0000%% fval =%??? -78%% 例題2c = [0.04 0.15 0.1 0.125]';?A = [-0.03 -0.3 0 -0.15;0.14 0 0 0.07];b = [-32 42]';Aeq = [0.05 0 0.2 0.1];beq = 24;lb = [0 0 0 0]';[x fval] = linprog(c, A, b, Aeq, beq, lb)% x =%????????? 0%?? 106.6667%?? 120.0000%????????? 0%% fval =%???? 28% 這個題可能有多個解，即有多個x可以使得目標函數的最小值為28（不同的Matlab版本可能得到的x的值不同，但最后的最小值一定是28）% 例如我們更改一個限定條件：令x1要大于0（注意Matlab中線性規劃的標準型要求的不等式約束的符號是小于等于0）% x1 >0? 等價于? -x1 < 0，那么給定 -x1 <= -0.1 (根據實際問題可以給一個略小于0的數-0.1)，這樣能將小于號轉換為小于等于號，滿足Matlab的標準型c = [0.04 0.15 0.1 0.125]';?A = [-0.03 -0.3 0 -0.15;0.14 0 0 0.07-1 0 0 0];b = [-32 42 -0.1]';Aeq = [0.05 0 0.2 0.1];beq = 24;lb = [0 0 0 0]';[x fval] = linprog(c, A, b, Aeq, beq, lb)% x =%???? 0.1000%?? 106.6567%?? 119.9750%????????? 0%% fval =%??? 28.0000%% 例題3c = [-2 -3 5]';A = [-2 5 -1;1 3 1];b = [-10 12];Aeq = ones(1,3);beq = 7;lb = zeros(3,1);[x fval] = linprog(c, A, b, Aeq, beq, lb)fval = -fval % 注意這個fval要取負號（原來是求最大值，我們添加負號變成了最小值問題）% x =%???? 6.4286%???? 0.5714%????????? 0% fval =%?? -14.5714% fval =%??? 14.5714%% 多個解的情況% 例如 ： min z = x1 + x2?? s.t.? x1 + x2 >= 10c = [1 1]';??A = [-1 -1];b = -10;[x fval] = linprog(c, A, b)?? % Aeq, beq, lb和ub我們都沒寫，意味著沒有等式約束和上下界約束% x有多個解時，Matlab會給我們返回其中的一個解%% 不存在解的情況% 例如 ： min z = x1 + x2?? s.t.? x1 + x2 = 10 、 x1 + 2*x2 <= 8、 x1 >=0 ，x2 >=0c = [1 1]';A = [1 2];b = 8;Aeq = [1 1];beq = 10;lb = [0 0]';[x fval] = linprog(c, A, b, Aeq, beq, lb)? % Linprog stopped because no point satisfies the constraints.（沒有任何一個點滿足約束條件）

整數規劃：

整數規劃（Integer Programming, IP）是一種數學規劃方法，其中決策變量被限制為整數值。整數規劃是線性規劃的擴展，旨在解決需要在整數取值范圍內做出決策的問題。

整數規劃的一般形式可以表示為：

最小化（或最大化）目標函數：

[ f(x) ]

在給定約束條件下，求解決策變量 ( x ) 的最優整數解。

約束條件包括等式約束和不等式約束，可以表示為：

等式約束：

[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]

不等式約束：

[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]

其中， ( gi(x) ) 和 ( hj(x) ) 為函數，與決策變量 ( x ) 有關。

整數規劃問題在實際應用中非常常見，因為存在許多情況下必須做出離散（整數）決策的需要。例如，裝載問題中需要決定將貨物裝在哪輛卡車上；制定生產計劃時需要決定生產數量；旅行商問題中需要選擇訪問的城市順序等。

整數規劃的求解方法相較于線性規劃更為困難，因為整數域的離散性質增加了問題的復雜性。常見的整數規劃求解方法包括分支定界法（Branch and Bound）、割平面法（Cutting Plane）、啟發式算法（Heuristic Algorithms）等。

在實際問題中，常常需要將問題轉化為整數規劃模型，并利用整數規劃方法求解最優解。整數規劃的應用廣泛，涵蓋了物流、生產管理、航空航天、金融投資等眾多領域。

Matlzb中的操作：

與線性規劃操作相比添加一項整數向量，在約束條件中目標函數中那個自變量xn是整數就將他的下標寫在intcon中。

?

?

?

代碼參考：

%% 線性整數規劃問題%% 例1c=[-20,-10]';intcon=[1,2];? % x1和x2限定為整數A=[5,4;2,5];b=[24;13];lb=zeros(2,1);?[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)fval = -fval%% 例2c=[18,23,5]';intcon=3;? % x3限定為整數A=[107,500,0;72,121,65;-107,-500,0;-72,-121,-65];b=[50000;2250;-500;-2000];lb=zeros(3,1);[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)%% 例3c=[-3;-2;-1]; intcon=3; % x3限定為整數A=ones(1,3); b=7;Aeq=[4 2 1]; beq=12;lb=zeros(3,1); ub=[+inf;+inf;1]; %x(3)為0-1變量[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)

0-1規劃經典例題：

背包問題：

?

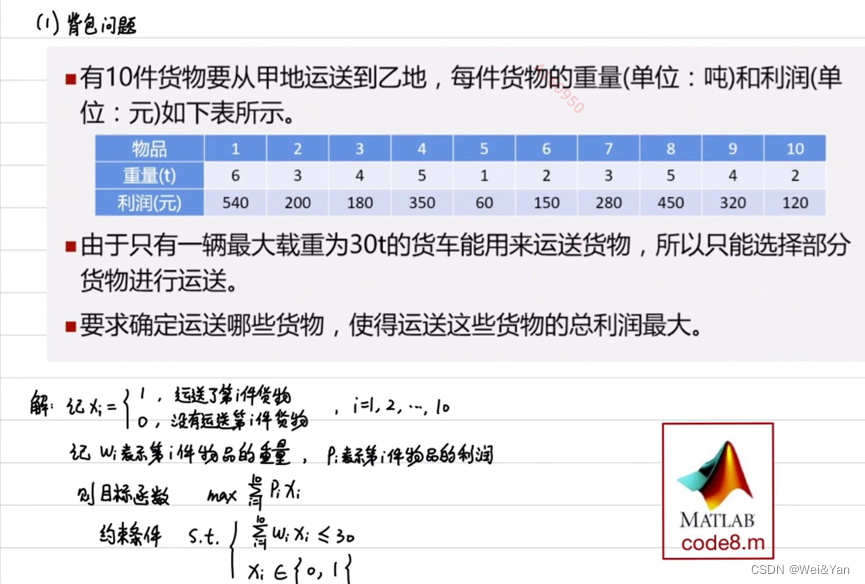
指派問題：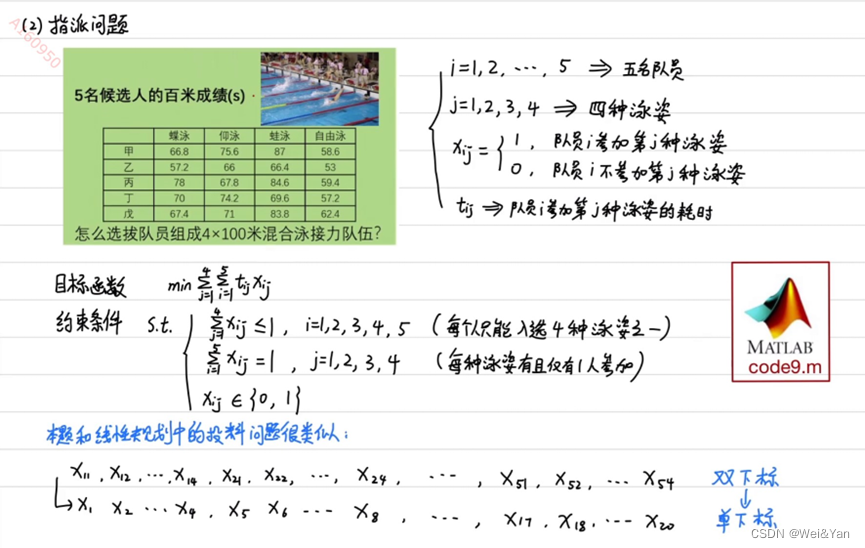

?

參考代碼：

背包問題：
%% 背包問題（貨車運送貨物的問題）
c = -[540 200 180 350 60 150 280 450 320 120];  % 目標函數的系數矩陣(最大化問題記得加負號)
intcon=[1:10];  % 整數變量的位置(一共10個決策變量，均為0-1整數變量)
A = [6 3 4 5 1 2 3 5 4 2];  b = 30;   % 線性不等式約束的系數矩陣和常數項向量（物品的重量不能超過30）
Aeq = []; beq =[];  % 不存在線性等式約束
lb = zeros(10,1);  % 約束變量的范圍下限
ub = ones(10,1);  % 約束變量的范圍上限
%最后調用intlinprog()函數
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
fval = -fval

?

%% 指派問題（選擇隊員去進行游泳接力比賽）
clear;clc
c = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]';  % 目標函數的系數矩陣（先列后行的寫法）
intcon = [1:20];  % 整數變量的位置(一共20個決策變量，均為0-1整數變量)
% 線性不等式約束的系數矩陣和常數項向量（每個人只能入選四種泳姿之一，一共五個約束）
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
% A = zeros(5,20);
% for i = 1:5
%     A(i, (4*i-3): 4*i) = 1;
% end
b = [1;1;1;1;1];
% 線性等式約束的系數矩陣和常數項向量 （每種泳姿有且僅有一人參加，一共四個約束）
Aeq = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)];  % 或者寫成 repmat(eye(4),1,5)  
beq = [1;1;1;1];
lb = zeros(20,1);  % 約束變量的范圍下限
ub = ones(20,1);  % 約束變量的范圍上限
%最后調用intlinprog()函數
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% reshape(x,4,5)'
%      0     0     0     1    甲自由泳
%      1     0     0     0    乙蝶泳
%      0     1     0     0    丙仰泳
%      0     0     1     0    丁蛙泳
%      0     0     0     0    戊不參加

?

非線性規劃：

非線性規劃（Nonlinear Programming, NLP）是一種數學規劃方法，用于解決目標函數或約束條件具有非線性項的優化問題。與線性規劃不同，非線性規劃包含了更為復雜的數學模型和求解過程。

一般形式的非線性規劃可以表示為：

最小化（或最大化）目標函數：

[ f(x) ]

在給定約束條件下，求解決策變量 ( x ) 的最優解。

約束條件包括等式約束和不等式約束，可以表示為：

等式約束：

[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]

不等式約束：

[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]

其中， ( gi(x) ) 和 ( hj(x) ) 是函數，與決策變量 ( x ) 相關。

非線性規劃的求解相對于線性規劃更為困難，因為非線性函數引入了非凸性、多個局部最優解等問題。求解非線性規劃通常需要使用迭代和數值優化方法，以逐步逼近全局最優解或局部最優解。

常見的非線性規劃求解方法包括：

1.牛頓法（Newton's Method）：基于二階導數信息進行迭代，可快速逼近局部最優解，但對初始點的選取敏感。

2.擬牛頓法（Quasi-Newton Methods）：通過逐步逼近黑塞矩陣（Hessian Matrix），避免了計算二階導數，常用的擬牛頓法包括DFP、BFGS等。

3.共軛梯度法（Conjugate Gradient Method）：針對特定類型的二次優化問題，具有收斂速度快的特點。

4.遺傳算法（Genetic Algorithms）：基于生物進化的思想，通過模擬遺傳、交叉和變異等操作，搜索最優解的全局性質。

5.粒子群優化（Particle Swarm Optimization）：模擬鳥群或魚群的行為，通過粒子的移動和信息共享來尋找最優解。

非線性規劃在實際問題中廣泛使用，包括經濟學、工程設計、數據擬合、機器學習等領域。通過合適的數值優化算法和合理的問題建模，可以求解非線性規劃問題并得到最優解。

?

Matlab求解：

?

?

?

列題：

參考代碼：?

主函數：

%% 非線性規劃的函數
% [x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
% x0表示給定的初始值（用行向量或者列向量表示），必須得寫
% A b表示線性不等式約束
% Aeq beq 表示線性等式約束
% lb ub 表示上下界約束
% @fun表示目標函數
% @nonlfun表示非線性約束的函數
% option 表示求解非線性規劃使用的方法
clear;clc
format long g   %可以將Matlab的計算結果顯示為一般的長數字格式（默認會保留四位小數，或使用科學計數法）%% 例題1的求解
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
% s.t. -(x1-1)^2 +x2 >= 0 ;  2x1-3x2+6 >= 0
x0 = [0 0];  %任意給定一個初始值 
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)  % 注意 fun1.m文件和nonlfun1.m文件都必須在當前文件夾目錄下
fval = -fval
% 一個值得討論的地方，能不能把線性不等式約束Ax <= b也寫到nonlfun1函數中？
% 先把nonlfun1中的c改為下面這樣：
% c = [(x(1)-1)^2-x(2); 
%        -2*x(1)+3*x(2)-6];
%  [x,fval] = fmincon(@fun1,x0,[],[],[],[],[],[],@nonlfun1)
% 結果也是可以計算出來的，但并不推薦這樣做~%% 使用其他算法對例題1求解
% edit fmincon  % 查看fmincon的“源代碼”
% Matlab2017a默認使用的算法是'interior-point' 內點法
% 使用interior point算法 （內點法）
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  
fval = -fval
% 使用SQP算法 （序列二次規劃法）
option = optimoptions('fmincon','Algorithm','sqp')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  
fval = -fval   %得到-4.358，遠遠大于內點法得到的-1,猜想是初始值的影響
% 改變初始值試試
x0 = [1 1];  %任意給定一個初始值 
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  % 最小值為-1，和內點法相同（這說明內點法的適應性要好）
fval = -fval  
% 使用active set算法 （有效集法）
option = optimoptions('fmincon','Algorithm','active-set')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval  
% 使用trust region reflective (信賴域反射算法)
option = optimoptions('fmincon','Algorithm','trust-region-reflective')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  
fval = -fval  
% this algorithm does not solve problems with the constraints you have specified. 
% 這說明這個算法不適用我們這個約束條件，所以以后遇到了不能求解的情況，記得更換其他算法試試！！！%% 選取初始值得到的結果可能會不滿足限定條件，出現了一個Bug 因此選擇的初始值很重要
x0 = [40.8, 10.8];
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  
fval = -fval  
% https://cn.mathworks.com/help/optim/ug/fmincon.html%% 生成不同的隨機初始值來優化代碼，有一定幾率會觸發上面那個Bug，因此不推薦
n = 10;  % 重復n次
Fval = +inf; X = [0,0];  %初始化最優的結果
A = [-2 3]; b = 6;
for i = 1:nx0 = [rand()*10 , rand()*10];  %用隨機數生成一個初始值（隨機數的范圍自己根據題目條件設置） [x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option); % 注意 fun1.m文件和nonlfun1.m文件都必須在當前文件夾目錄下if fval < Fval  % 如果找到了更小的值，那么就代替最優的結果Fval = fval;X = x;end
end
Fval = -Fval
X%% 使用蒙特卡羅的方法來找初始值(推薦）
clc,clear;
n=10000000; %生成的隨機數組數
x1=unifrnd(-100,100,n,1);  % 生成在[-100,100]之間均勻分布的隨機數組成的n行1列的向量構成x1
x2=unifrnd(-100,100,n,1);  % 生成在[-100,100]之間均勻分布的隨機數組成的n行1列的向量構成x2
fmin=+inf; % 初始化函數f的最小值為正無窮（后續只要找到一個比它小的我們就對其更新）
for i=1:nx = [x1(i), x2(i)];  %構造x向量, 這里千萬別寫成了：x =[x1, x2]if ((x(1)-1)^2-x(2)<=0)  & (-2*x(1)+3*x(2)-6 <= 0)     % 判斷是否滿足條件result = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ;  % 如果滿足條件就計算函數值if  result  < fmin  % 如果這個函數值小于我們之前計算出來的最小值fmin = result;  % 那么就更新這個函數值為新的最小值x0 = x;  % 并且將此時的x1 x2更新為初始值endend
end
disp('蒙特卡羅選取的初始值為：'); disp(x0)
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)
fval = -fval  %% 例題二的求解
x0 = [1 1 1];  %任意給定一個初始值 
lb = [0 0 0];  % 決策變量的下界
[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2)  % 注意 fun2.m文件和nonfun2.m文件都必須在當前文件夾目錄下
% x =
%          0.552167405729277          1.20325915507969         0.947824046150443
% fval =
%           10.6510918606939%% 使用蒙特卡羅的方法來找初始值(推薦）
clc,clear;
n=1000000; %生成的隨機數組數
x1= unifrnd(0,2,n,1);   % 生成在[0,2]之間均勻分布的隨機數組成的n行1列的向量構成x1
x2 = sqrt(2-x1);  % 根據非線性等式約束用x1計算出x2
x3 = sqrt((3-x2)/2); % 根據非線性等式約束用x2計算出x3
fmin=+inf; % 初始化函數f的最小值為正無窮（后續只要找到一個比它小的我們就對其更新）
for i=1:nx = [x1(i), x2(i), x3(i)];  %構造x向量, 這里千萬別寫成了：x =[x1, x2, x3]if (-x(1)^2+x(2)-x(3)^2<=0) & (x(1)+x(2)^2+x(3)^2-20<=0)   % 判斷是否滿足條件result =sum(x.*x) + 8 ;  % 如果滿足條件就計算函數值if  result  < fmin  % 如果這個函數值小于我們之前計算出來的最小值fmin = result;  % 那么就更新這個函數值為新的最小值x0 = x;  % 并且將此時的x1 x2 x3更新為初始值endend
end
disp('蒙特卡羅選取的初始值為：'); disp(x0)
lb = [0 0 0];  % 決策變量的下界
[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2)  % 注意 fun2.m文件和nonfun2.m文件都必須在當前文件夾目錄下%% 例題三的求解(蒙特卡羅模擬那一講的例題)
clear;clc
% 蒙特卡羅模擬得到的最大值為3445.6014
% 最大值處x1 x2 x3的取值為：
%           22.5823101903968          12.5823101903968          12.1265223966757
A = [1 -2 -2;  1 2 2];  b = [0 72];
x0 = [ 22.58   12.58  12.13];
Aeq = [1 -1 0]; beq = 10;
lb = [-inf 10 -inf];  ub = [inf 20 inf];  
[x,fval] = fmincon(@fun3,x0,A,b,Aeq,beq,lb,ub,[])  % 注意沒有非線性約束，所以這里可以用[]替代，或者干脆不寫
fval = -fval

fun1-3：

function f = fun1(x)% 注意：這里的f實際上就是目標函數，函數的返回值也是f% 輸入值x實際上就是決策變量，由x1和x2組成的向量% fun1是函數名稱，到時候會被fmincon函數調用, 可以任意取名% 保存的m文件和函數名稱得一致，也要為fun1.m
%      max  f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ; 
endfunction f = fun2(x)%     f = x(1)^2+x(2)^2 +x(3)^2+8 ; f = sum(x.*x) + 8;  % 可別忘了x實際上是一個向量，我們可以使用矩陣的運算符號對其計算
endfunction f = fun3(x)f = -prod(x);  % 可別忘了x實際上是一個向量（prod表示連乘符號，用法和sum類似）
end

?nonlfun1-2：

function [c,ceq] = nonlfun1(x)% 注意：這里的c實際上就是非線性不等式約束，ceq實際上就是非線性等式約束% 輸入值x實際上就是決策變量，由x1和x2組成的一個向量% 返回值有兩個，一個是非線性不等式約束c，一個是非線性等式約束ceq% nonlfun1是函數名稱，到時候會被fmincon函數調用, 可以任意取名，但不能和目標函數fun1重名% 保存的m文件和函數名稱得一致，也要為nonlfun1.m
%     -(x1-1)^2 +x2 >= 0 c = [(x(1)-1)^2-x(2)];   % 千萬別寫成了: (x1-1)^2 -x2ceq = [];  % 不存在非線性等式約束，所以用[]表示
endfunction [c,ceq] = nonlfun2(x)% 非線性不等式約束c = [-x(1)^2+x(2)-x(3)^2;   % 一定要注意寫法的規范，再次強調這里的x是一個向量！不能把x(1)寫成x1x(1)+x(2)^2+x(3)^2-20];% 非線性等式約束ceq = [-x(1)-x(2)^2+2;x(2)+2*x(3)^2-3]; 
end

?

最大最小化模型：

在最不利的條件下求最有利的模型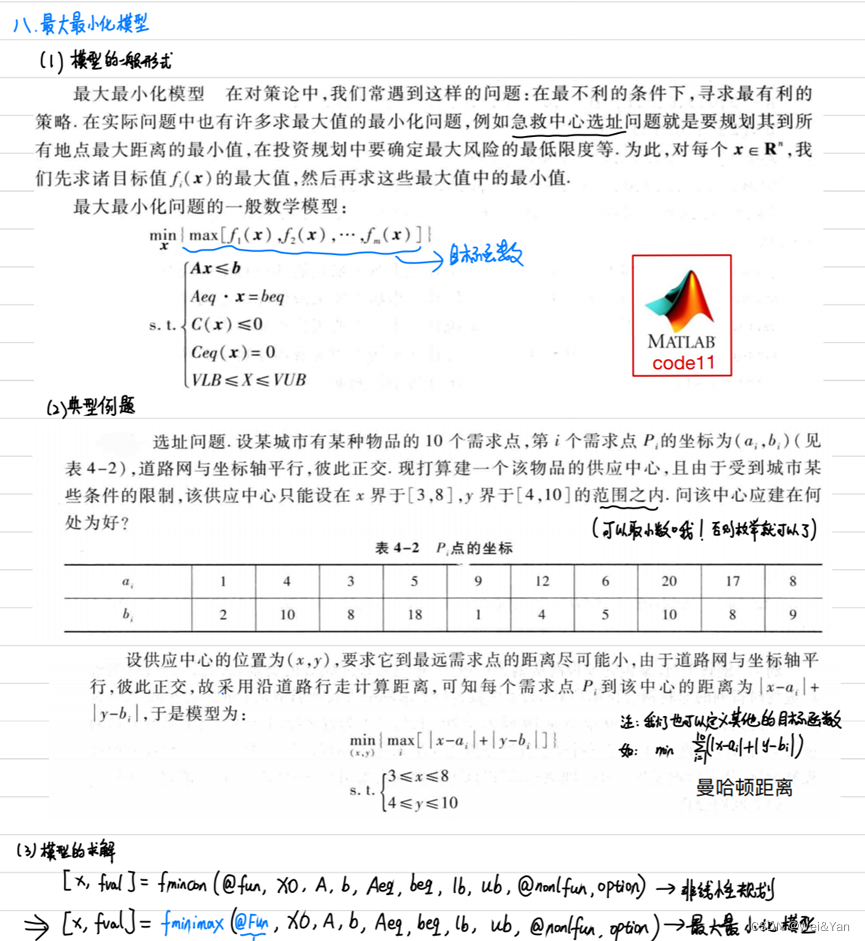

?

參考代碼：

%% 最大最小化模型  :   min{max[f1,f2,···,fm]}
x0 = [6, 6];      % 給定初始值
lb = [3, 4];  % 決策變量的下界
ub = [8, 10];  % 決策變量的上界
[x,feval] = fminimax(@Fun,x0,[],[],[],[],lb,ub)
max(feval)
% x =
%     8.0000    8.5000
% feval =
%    13.5000    5.5000    5.5000   12.5000    8.5000    8.5000    5.5000   13.5000    9.5000    0.5000
% 結論：
% 在坐標為(8,8.5)處建立供應中心可以使該點到各需求點的最大距離最小，最小的最大距離為13.5單位。

?fun：

%兩種求曼哈頓距離方法：
function f = Fun(x)a=[1 4 3 5 9 12 6 20 17 8];b=[2 10 8 18 1 4 5 10 8 9];%  函數向量f=zeros(10,1);for i = 1:10f(i) = abs(x(1)-a(i))+abs(x(2)-b(i));  end
% f(1) = abs(x(1)-a(1))+abs(x(2)-b(1));  
% f(2) = abs(x(1)-a(2))+abs(x(2)-b(2));
% f(3) = abs(x(1)-a(3))+abs(x(2)-b(3));
% f(4) = abs(x(1)-a(4))+abs(x(2)-b(4));
% f(5) = abs(x(1)-a(5))+abs(x(2)-b(5));
% f(6) = abs(x(1)-a(6))+abs(x(2)-b(6));
% f(7) = abs(x(1)-a(7))+abs(x(2)-b(7));
% f(8) = abs(x(1)-a(8))+abs(x(2)-b(8));
% f(9) = abs(x(1)-a(9))+abs(x(2)-b(9));
% f(10) = abs(x(1)-a(10))+abs(x(2)-b(10));
end 

?

多目標規劃：

?

參考代碼：

%%  多目標規劃問題
w1 = 0.4;  w2 = 0.6;  % 兩個目標函數的權重  x1 = 5  x2 = 2
w1 = 0.5;  w2 = 0.5;  % 兩個目標函數的權重  x1 = 5  x2 = 2
w1 = 0.3;  w2 = 0.7;  % 兩個目標函數的權重  x1 = 1  x2 = 6
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3];  % 線性規劃目標函數的系數
A = [-1 -1];  b = -7; % 不等式約束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub)
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)%% 敏感性分析
clear;clc
W1 = 0.1:0.001:0.5;  W2 = 1- W1;  
n =length(W1);
F1 = zeros(n,1);  F2 = zeros(n,1);   X1 = zeros(n,1);  X2 = zeros(n,1);   FVAL = zeros(n,1);
A = [-1 -1];  b = -7; % 不等式約束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:nw1 = W1(i);  w2 = W2(i);c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3];  % 線性規劃目標函數的系數[x,fval] = linprog(c,A,b,[],[],lb,ub);F1(i) = 2*x(1)+5*x(2);F2(i) = 0.4*x(1) + 0.3*x(2);X1(i) = x(1);X2(i) = x(2);FVAL(i) = fval;
end% 「Matlab」“LaTex字符匯總”講解：https://blog.csdn.net/Robot_Starscream/article/details/89386748
% 在圖上可以加上數據游標，按住Alt加鼠標左鍵可以設置多個數據游標出來。
figure(1) 
plot(W1,F1,W1,F2)
xlabel('f_{1}的權重') 
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的權重') 
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')figure(3)
plot(W1,FVAL)  % 看起來是兩個直線組合起來的下半部分
xlabel('f_{1}的權重') 
ylabel('綜合指標的值')

?

?