回歸擬合：

分類

本文是作者的預測算法系列的第四篇，前面的文章中介紹了BP、SVM、RF及其優化，感興趣的讀者可以在作者往期文章中了解，這一篇將介紹——極限學習機

過去的幾十年里基于梯度的學習方法被廣泛用于訓練神經網絡，如BP算法利用誤差的反向傳播來調整網絡的權值.然而，由于不適當的學習步長，導致算法的收斂速度非常慢，容易產生局部最小值，因此往往需要進行大量迭代才能得到較為滿意的精度．這些問題，已經成為制約其在應用領域發展的主要瓶頸.

Huang等人［1］ 提出了一種簡單高效的單隱層前饋神經網絡學習算法，稱為極限學習機(extremelearning machine,ELM).其典型優勢是訓練的速度非常快，具有訓練速度快、復雜度低的優點，克服了傳統梯度算法的局部極小、過擬合和學習率的選擇不合適等[2]問題,目前被廣泛地應用于模式識別、故障診斷、機器學習、軟測量等領域。

00目錄

1 標準極限學習機ELM

2 代碼目錄

3 ELM的優化實現

4 源碼獲取

5 展望

參考文獻

01 標準極限學習機ELM

1.1 ELM原理

給定一數據集：T={(x1,y1),…,(xl,yl)}，其中xi∈Rn，y∈R，i=1,…,l；含有 N 個隱層節點，激勵函數為 G 的極限學習機回歸模型可表示為：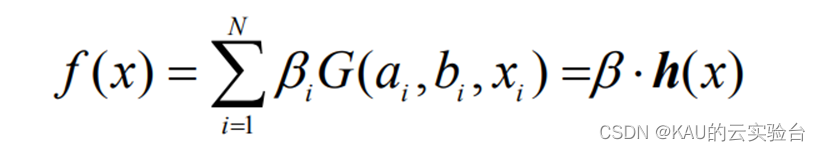

其中：bi 為第 i 個隱層節點與輸出神經元的輸出權值；ai為輸入神經元與第 i 個隱層節點的輸入權值；bi為第 i 個隱層節點的偏置；h(x)=[G(a1,b1,x1),…,(aN,bN,xN)]稱為隱層輸出矩陣。并且ai,bi在訓練開始時隨機選擇，且在訓練過程中保持不變。輸出權值可以通過求解下列線性方程組的最小二乘解來獲得：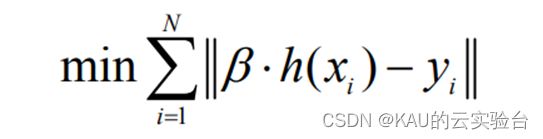

該方程組的最小二乘解為：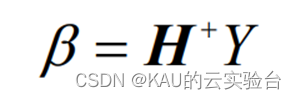

其中， H+稱為隱層輸出矩陣H的 Moore-Penrose 廣義逆.

1.2 ELM優化

由于 ELM 隨機給定輸入權值矩陣和隱含層偏差，由1.1節中的計算式可知輸出權值矩陣是由輸入權值矩陣和隱含層偏差計算得到的，可能會存在一些輸入權值矩陣和隱含層偏差為 0，即部分隱含層節點是無效的． 因此在某些實際應用中，ELM 需要大量的隱含層節點才能達到理想的精度． 并且 ELM 對未在訓練集中出現的樣本反應能力較差，即泛化能力不足。針對以上問題可利用優化算法和極限學習機網絡相結合的學習算法，即利用優化算法優化選擇極限學習機的輸入層權值和隱含層偏差，從而得到一個最優的網絡[3].

對于ELM優化，以PSO優化ELM為例，其流程如下所示：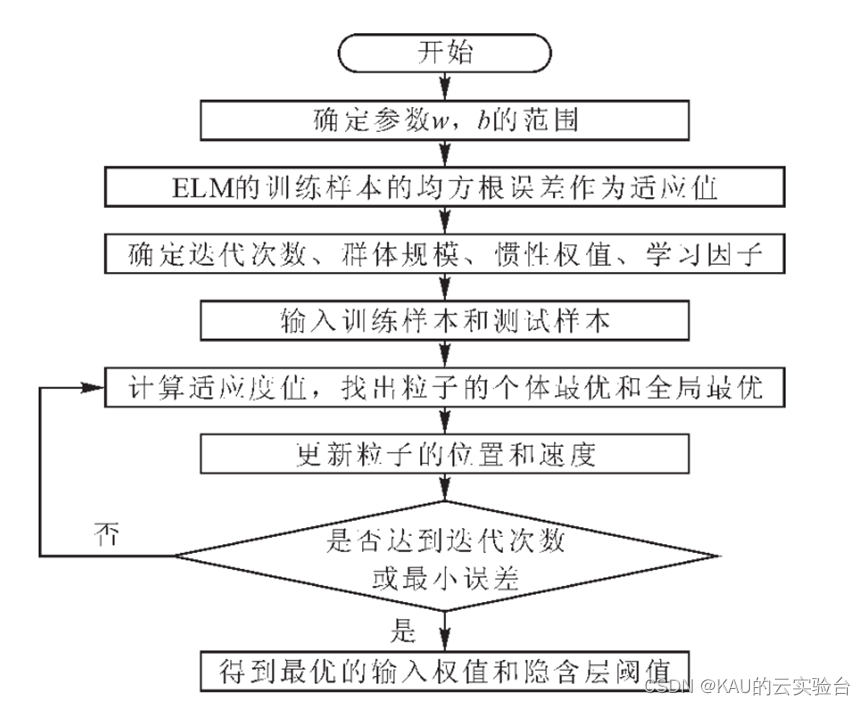

02 代碼目錄

本文以改進的動態多種群粒子群算法優化ELM，并與標準粒子群算法優化ELM和ELM算法進行對比。

改進的動態多種群粒子群優化算法（IDM-PSO）

分類問題：

其中，IDM_PSO_ELM.m、MY_ELM_CLA.m和PSO_ELM.m都是可獨立運行的主程序.而result.m可用于對比這三個算法的效果，若想對比算法，單獨運行這個程序即可。

部分源碼如下：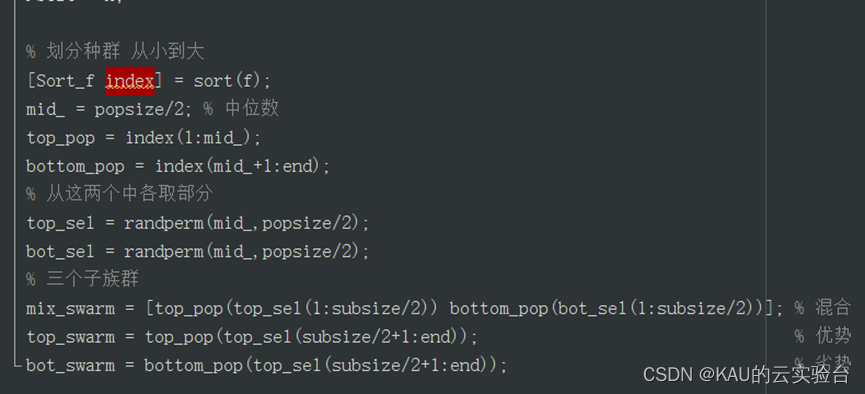

回歸擬合問題：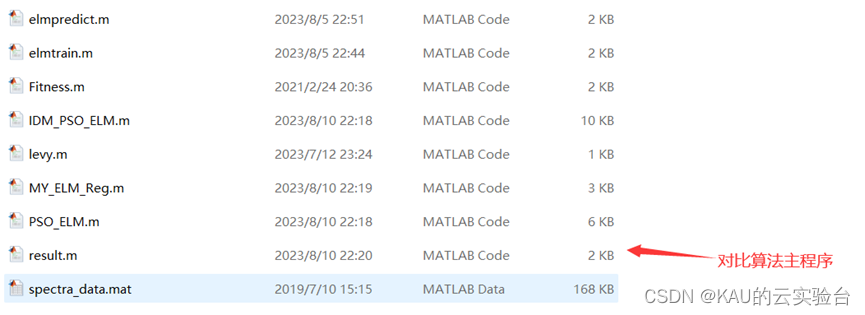

回歸擬合的程序和分類的類似，這里不再重復。

部分源碼：

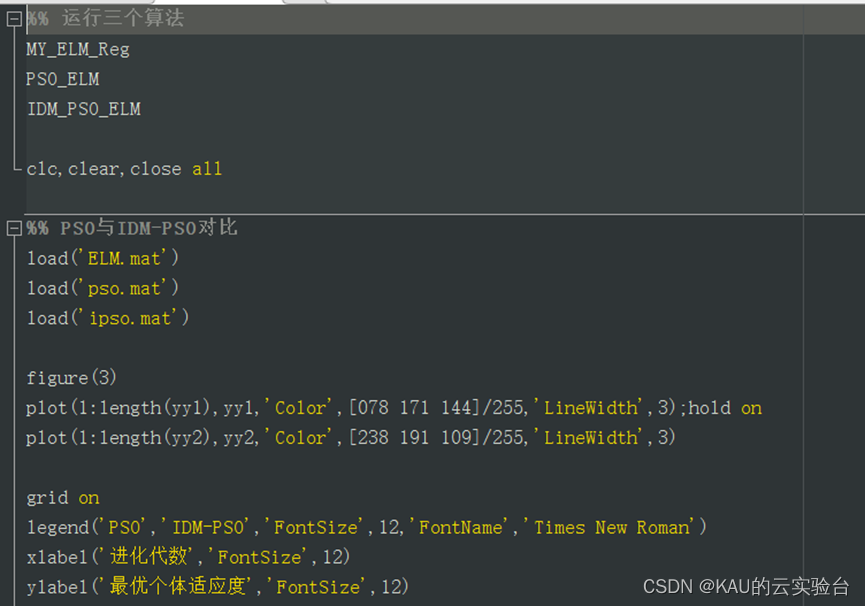
03 極限學習機及其優化的預測結果對比

3.1 回歸擬合

應用問題為多輸入單輸出問題。

3.1.1 評價指標

為了驗證所建模型的準確性和精度，分別采用均方根差(Root Mean Square Error，RMSE) 、平均絕對百分誤差( Mean Absolute Percentage Error，MAPE)和平均絕對值誤差( Mean Absolute Error，MAE) 作為評價標準。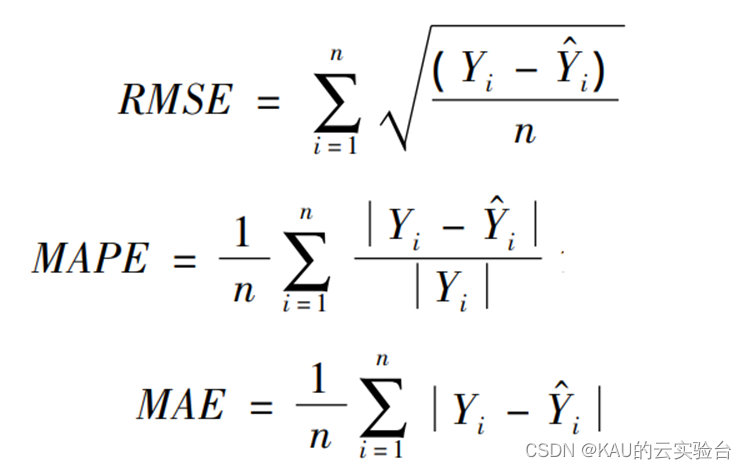

式中 Yi 和Y ^ i分別為真實值和預測值; n 為樣本數。

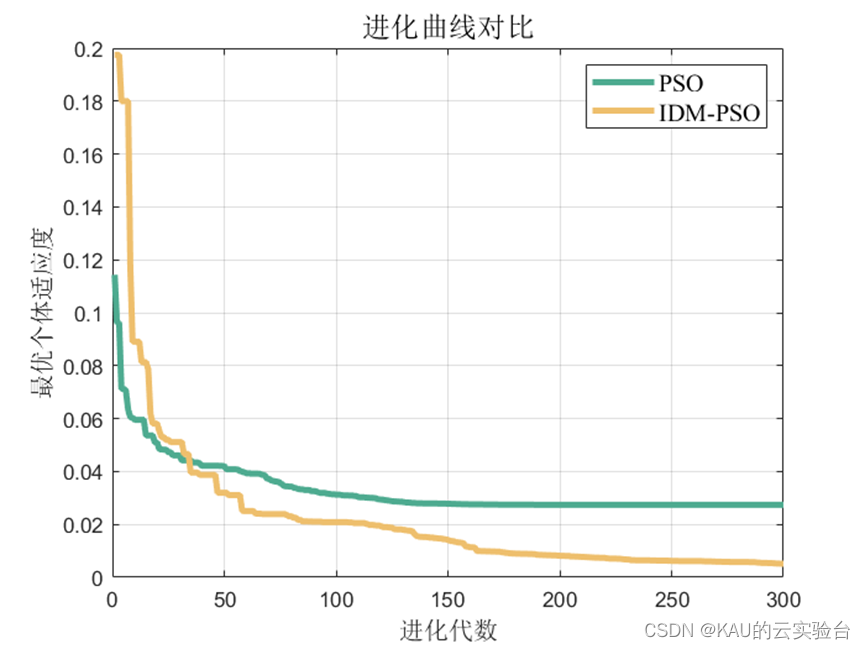
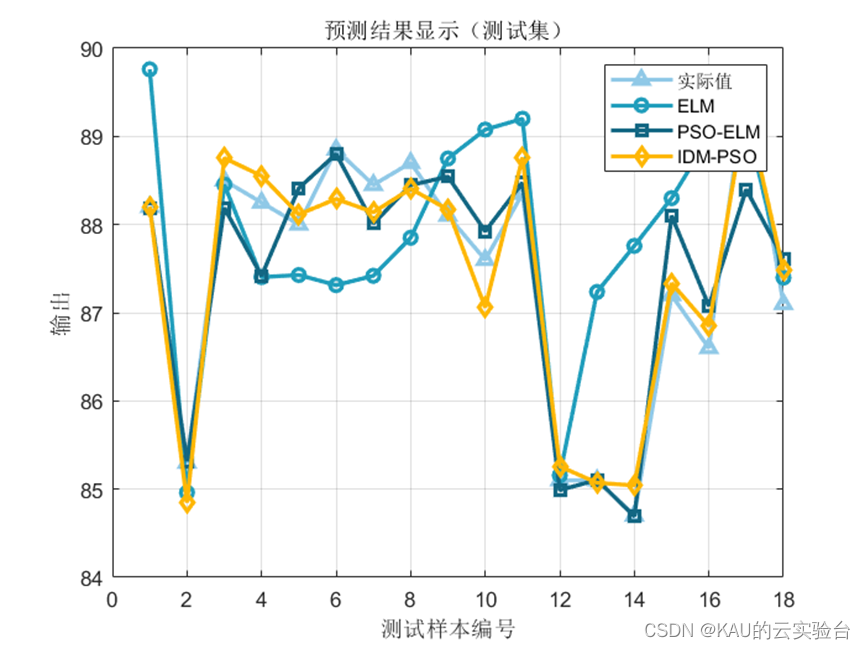
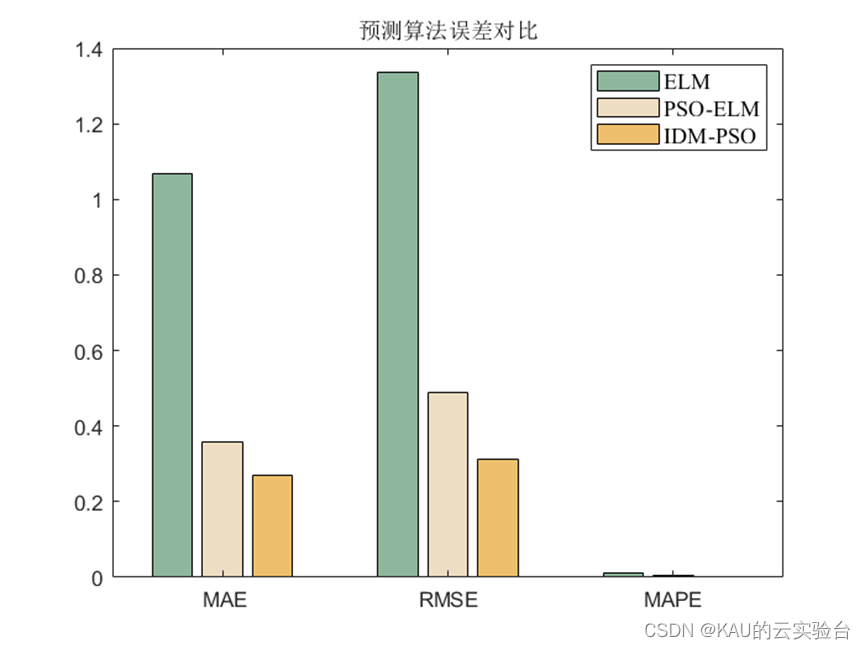
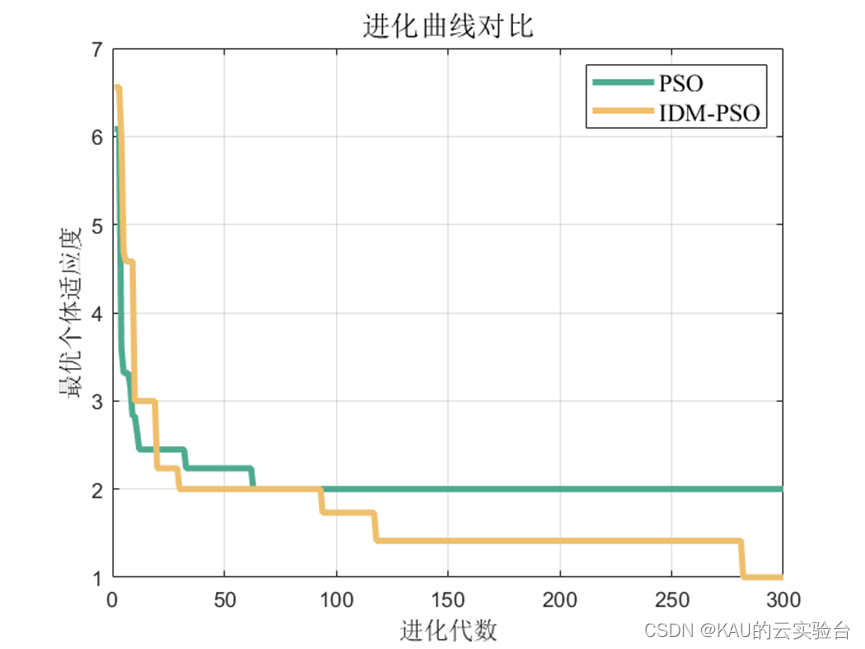
3.1.2 仿真結果

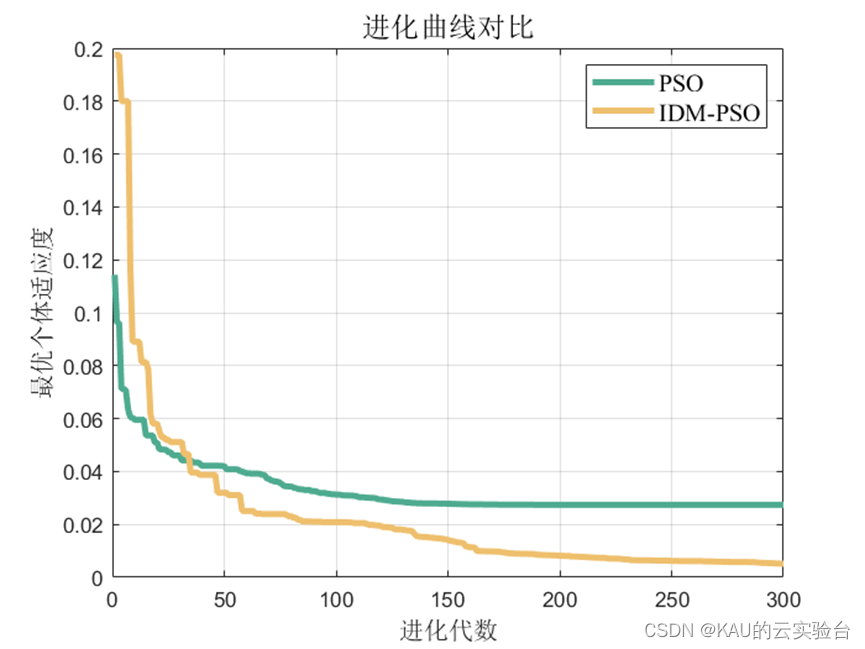
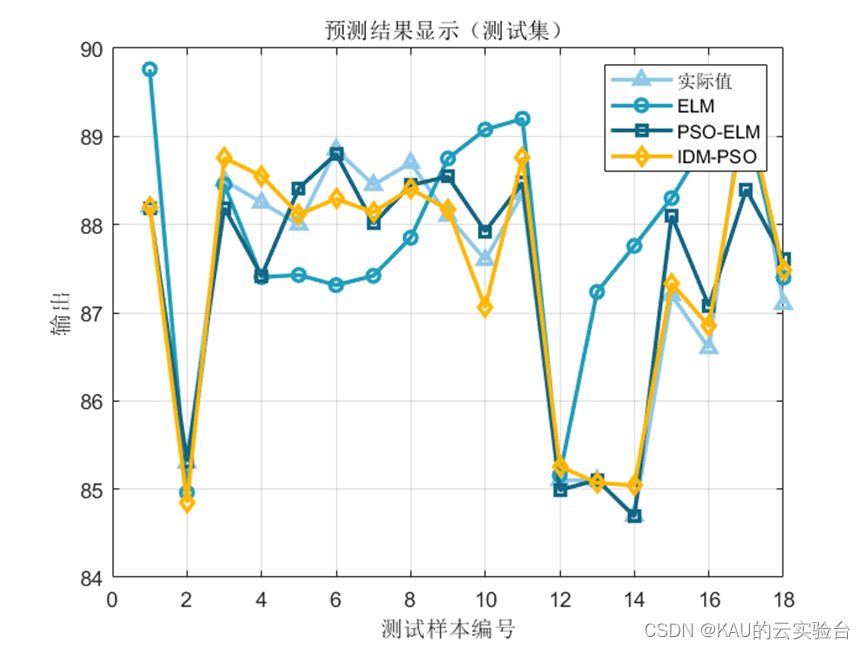
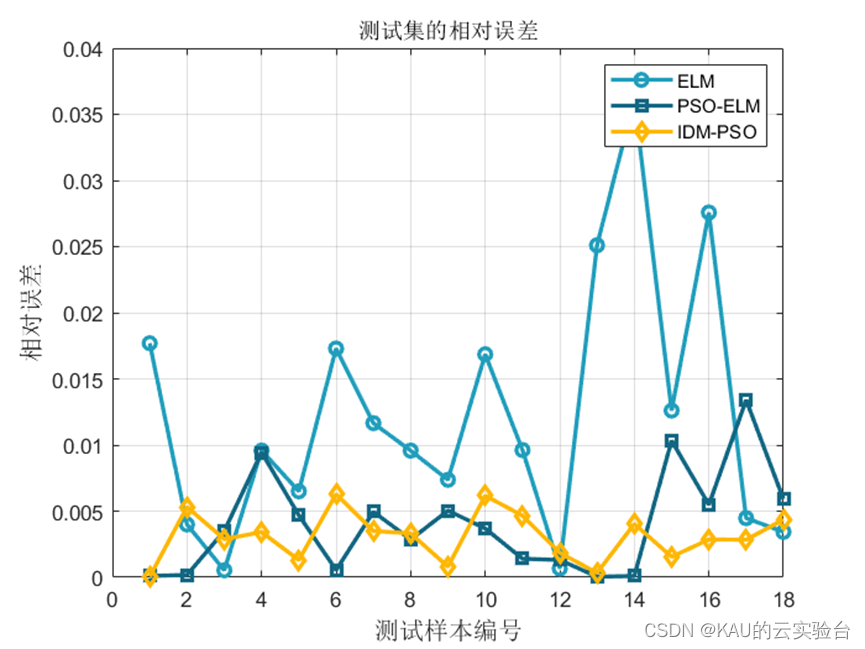
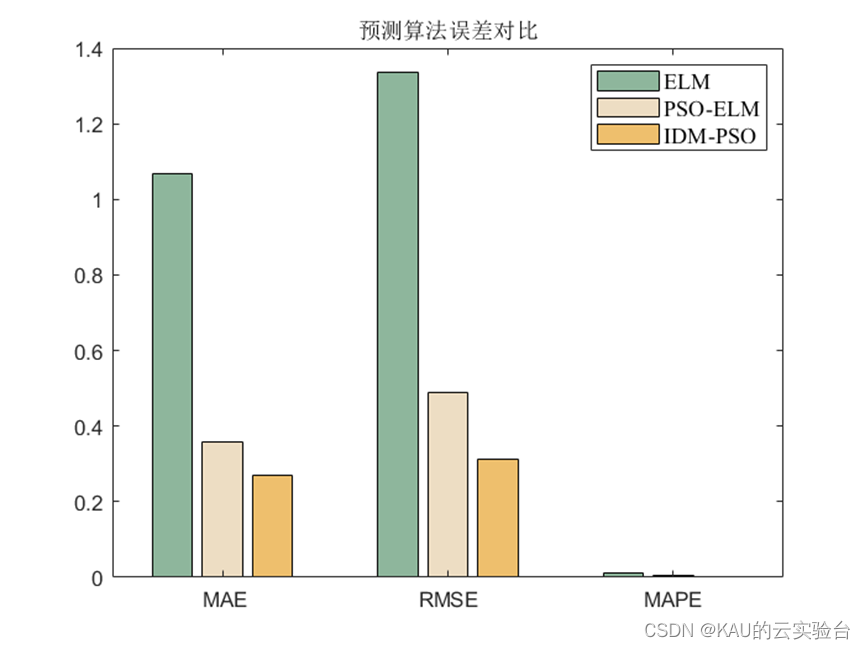
可以看出，優化是有效的。

3.2 分類

3.2.1 評價指標

為驗證模型準確率，本文從混淆矩陣、準確率、精確率、召回率、F1-score這些方面進行衡量。

1、混淆矩陣

混淆矩陣是一種可視化工具，混淆矩陣的每一列代表的是預測類別，其總數是分類器預測為該類別的數據總數，每一行代表了數據的真實類別，其總數是該類別下的數據實例總數。主對角線的元素即為各類別的分類準確的個數，通過混淆矩陣能夠直觀地看出多分類模型的分類準確率。

2、準確率

最為簡單判斷 SVM 多分類效果的方法就是用以下公式進行準確率r 的計算

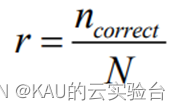
其中 ncorrect代表正確分類的樣本個數， N代表測試集中的樣本總數。

3、精確度

精度計算的是正類預測正確的樣本數，占預測是正類的樣本數的比例，公式如下

其中，TP表示的是正樣本被預測為正樣本的個數，FP表示的是負樣本被預測為 正樣本的個數。

4、召回率

召回率計算的是預測正類預測正確的樣本數，占實際是正類的樣本數的比例，公式如下：

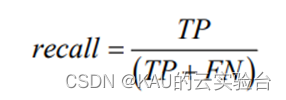
其中， FN 表示的是正樣本被判定為負樣本的個數。

5、F1-score

F1- score是精度和召回率的調和平均值， F1- score越高說明模型越穩健，計算公式為

6、宏平均（macro-averaging）

宏平均（macro-averaging）是指所有類別的每一個統計指標值的算數平均值， 也就是宏精確率（macro - precision），宏召回率（ macro -recall ），宏 F1 值 （macro- F1 score），其計算公式如下：

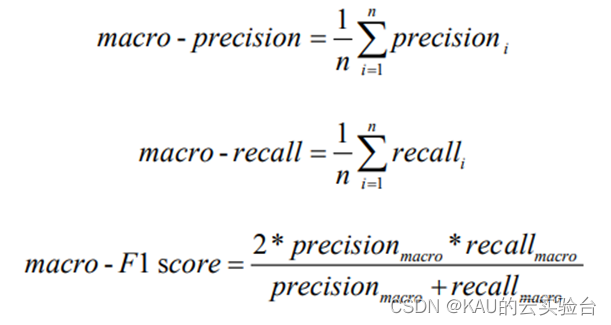
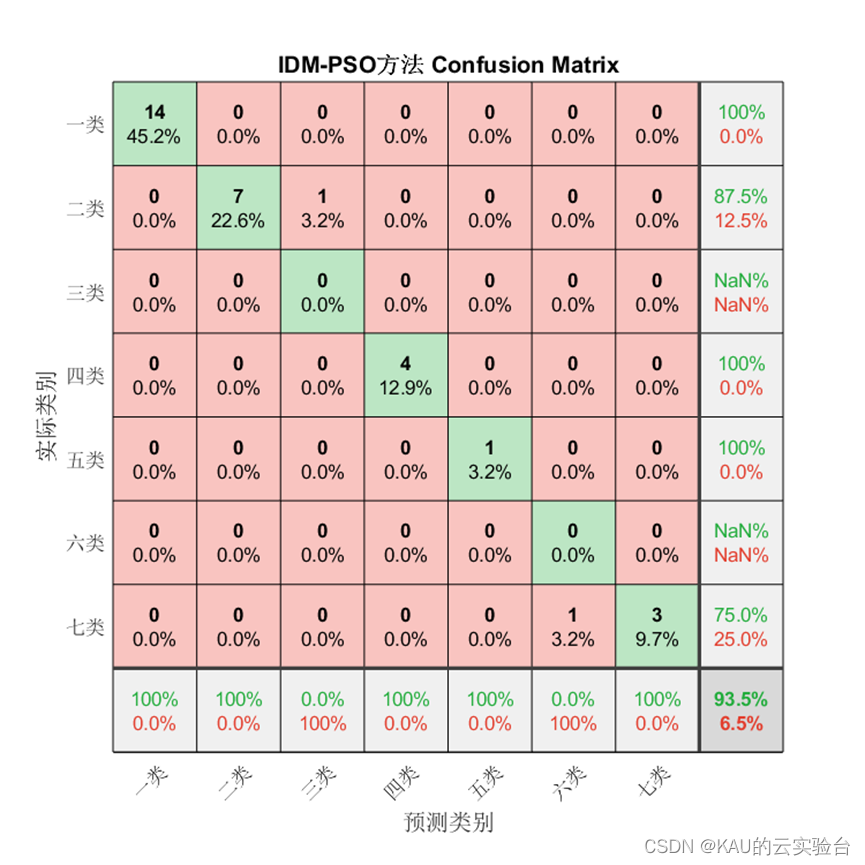
3.2.2 仿真結果

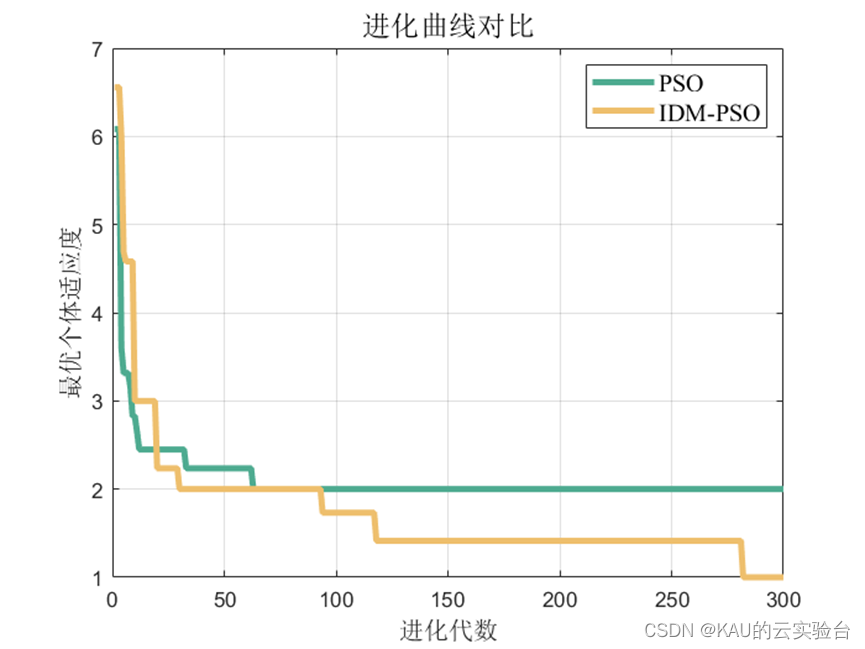
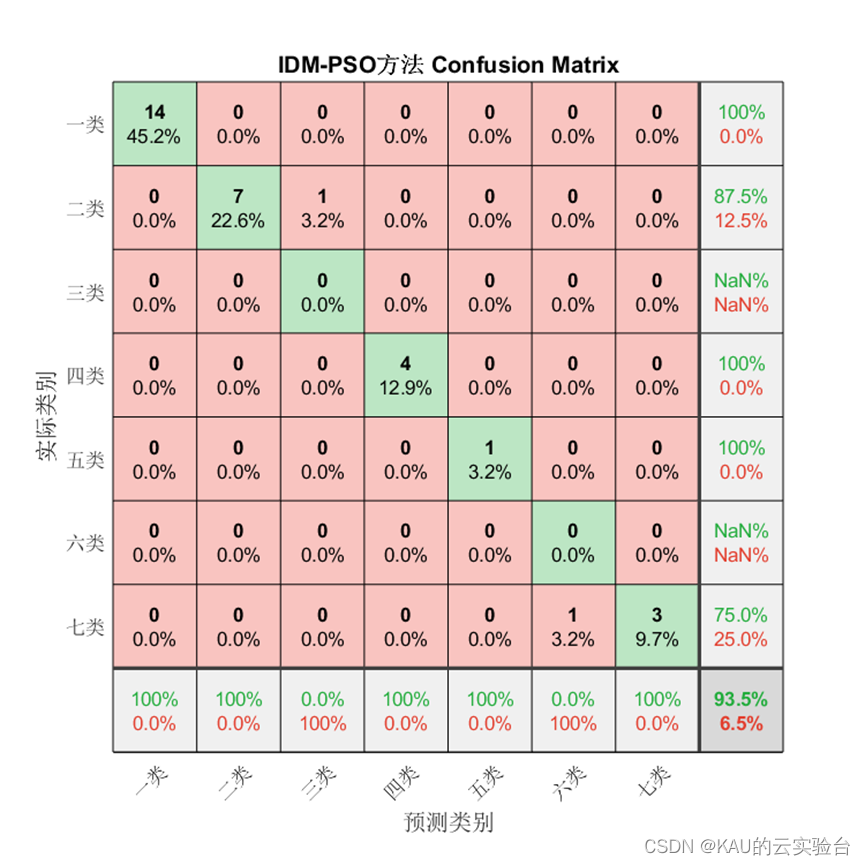
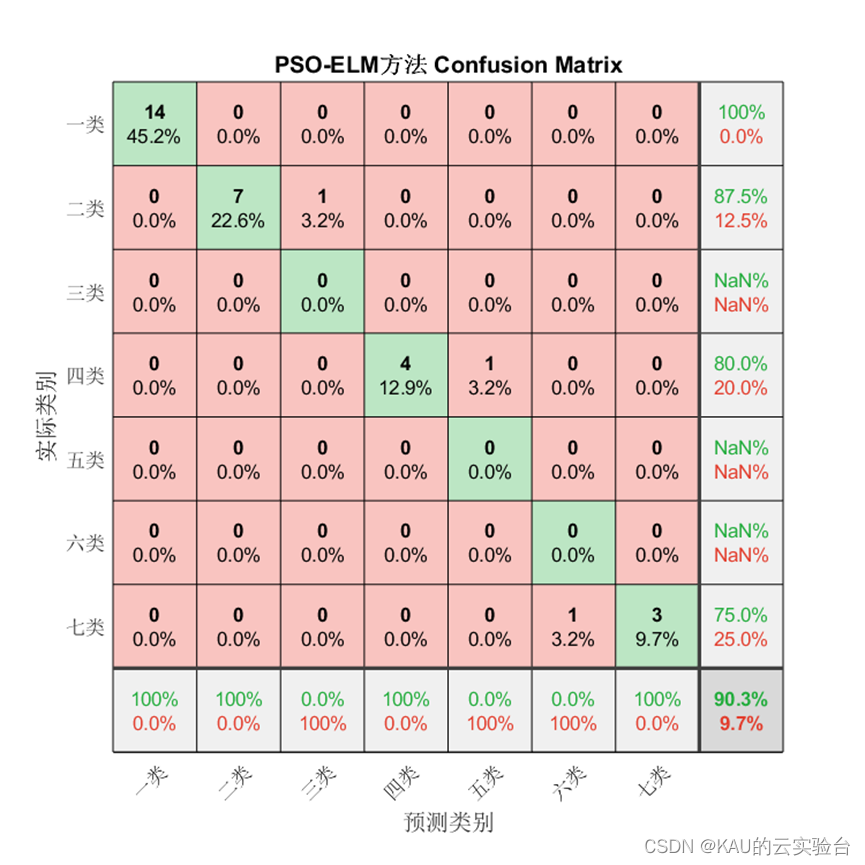
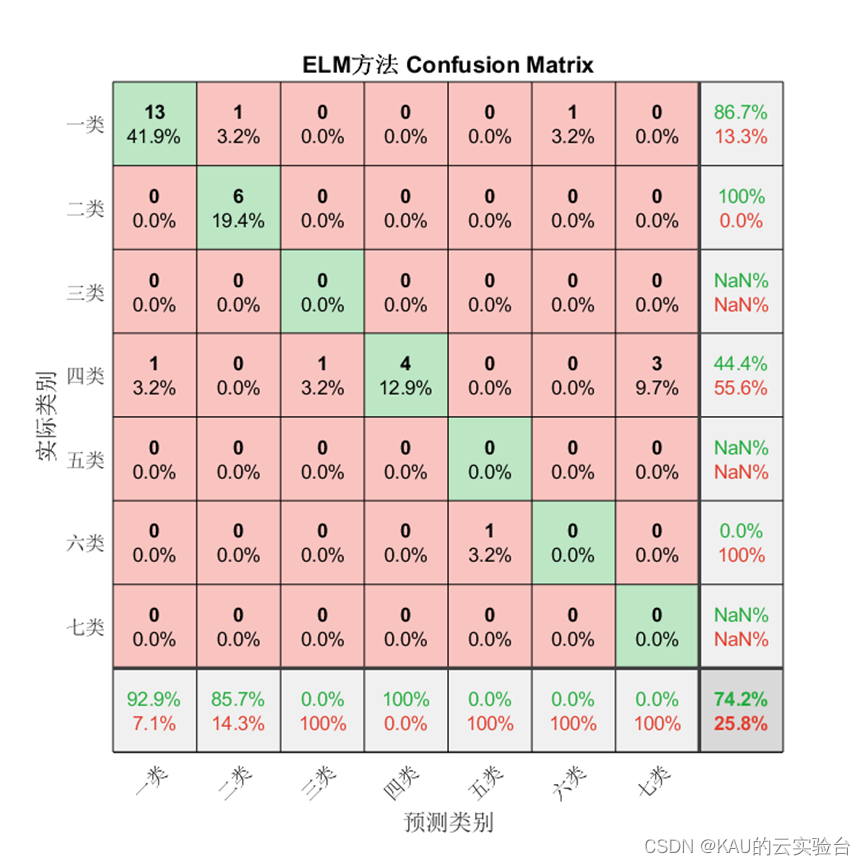
對于分類問題仍然有效，需要注意的是因為某些類別并沒有存在預測值，因此由精確率和F1的計算式可知會出現NaN。

04 源碼獲取

關注作者或私信

05 展望

本文介紹了應用改進的動態多種群粒子群算法優化ELM的案例，同樣也可以采用作者前面提到過的麻雀算法等，同時，極限學習機因其在處理大規模數據時出現的無法收斂等問題，出現了核極限學習機、多核極限學習機、深度極限學習機等變體，作者后續也會更新這些算法的實現。

參考文獻

[1]Huang G B，Zhu Q Y，Siew C K. Extreme learning machine:A new learning scheme of feedforward neural networks//Proceedings of the 2004 1EEE International Joint Conferenceon Neural Networks. Budapest，Hungary，2004:985-990

[2]FAN Shu-ming,QIN Xi-zhong,JIA Zhen-hong,et al.Time series forecasting based on ELM improved layered ensemble architecture[J].Computer Engineering and Design,2019,40(7):1915-1921.

[3]王杰,畢浩洋.一種基于粒子群優化的極限學習機[J].鄭州大學學報(理學版),2013,45(01):100-104.

另：如果有伙伴有待解決的優化問題（各種領域都可），可以發我，我會選擇性的更新利用優化算法解決這些問題的文章。

如果這篇文章對你有幫助或啟發，可以點擊右下角的贊(? ??_??)?(不點也行)，若有定制需求，可私信作者。