1- 題目: 已知一個DW

有圖中所示一行信息，表示一個DW(4字節,32位)
(一個word是兩個字節,所以DW(double word)就是4個字節)

已知 DW 值 payload=0x03000100

1.1 要求: 從DW中取出指定的位的值

分別取出P3，P2，P1，P0的值

P3表示該行中第[28:31]位的值
P2表示該行中第[24:27]位的值
P1表示該行中第[20:23]位的值
P0表示該行中第[16:19]位的值

1.1.1 分析

將DW的每一位的意義補充完整，得到該圖

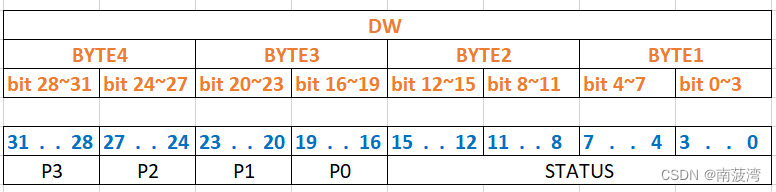
可以通過將DW的 值 payload 右移得到所需的指定 位 的值

payload = 0x03000100
(1)右移28位， 那么得到的值就只剩前4位，就是0x0,
也就是 bit[28:31]所指的值，就是P3, 即P3=0x0

(2)右移24位， 那么得到的值就只剩前8位，就是0x03,
也就是 bit[24:31]所指的值，就是P2和P3的值，只要和0xF相與，就能得到bit[24:27]的值，就是P2, 即P2=0x3

(3)右移20位， 那么得到的值就只剩前12位，就是0x030,
也就是 bit[20:31]所指的值，就是P1,P2和P3的值，只要和0xF相與，就能得到bit[20:23]的值，就是P1,即P1=0x0

(4)右移16位， 那么得到的值就只剩前16位，就是0x0300,
也就是 bit[16:31]所指的值，就是P0, P1, P2和P3的值，只要和0xF相與，就能得到bit[16:19]的值，就是P0, 即P0=0x0

1.1.2 實現

通過分析，可以得到如下的計算公式

P3_value = payload >> 28;
P2_value = payload >> 24 & 0xF;
p1_value = payload >> 20 & 0xF;
P0_value = payload >> 16 & 0xF;

1.1.3 簡化實現

上一項需要寫四行,比較麻煩

當P=3/2/1/0時, 合并這些重復,就是
P_value = payload >> (P+4)*4 & 0xF;

1.1.4 驗證

將payload的值 對應到每一位，并驗證P3/2/1/0值

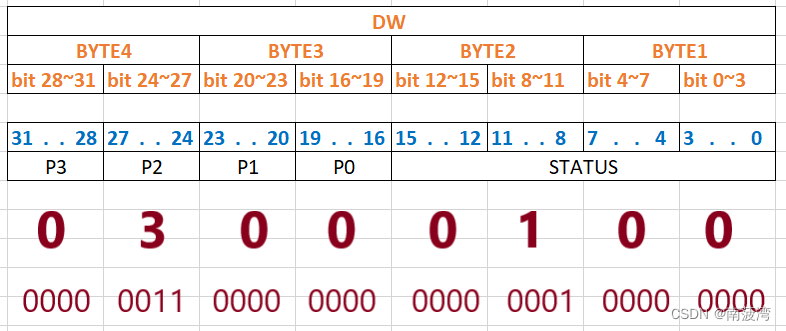
2- 題目: 已知一個DW

有圖中所示一行信息，表示一個DW(4字節,32位)
(一個word是兩個字節,所以DW(double word)就是4個字節)

已知 DW 值 payload=0x03000100

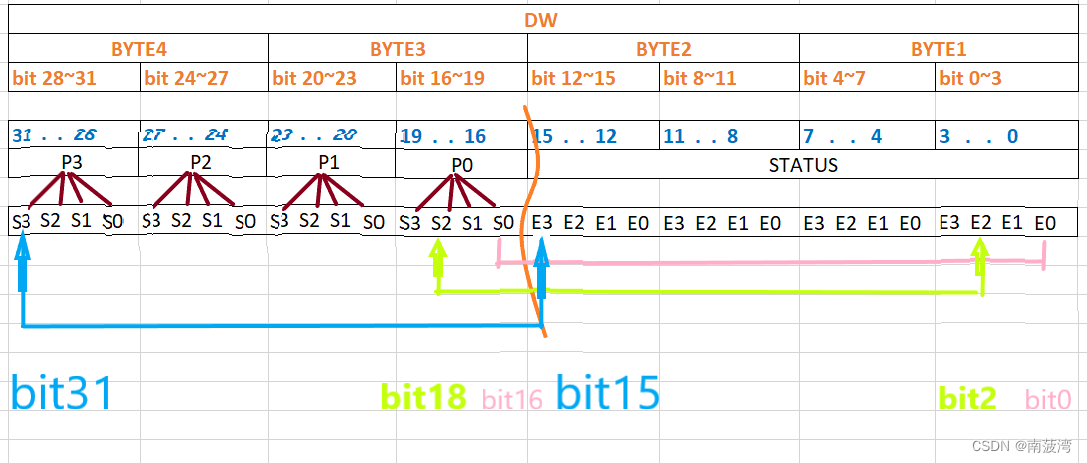
2.1 要求: 從DW中的指定的P和S,取出指定的位的值

已知DW的值payload=0x03000000
每一個P里面都有4個S,P和S都是隨機出現的，P和S結合后，就會生成一個數，有唯一的bit,
求這個bit對應的E中的bit的值，對應關系就是相差16個bit

2.1.1 分析

與P和S組合的bit 在E中的對應bit位 相差16個bit

在E中對應的bit計算公式
E_value_bit = P*4+S;

再將E右移對應的bit位，再與1相與，就能得到E對飲過的bit的值 E_value = E >> E_value_bit & 0x1;

2.1.2 實現

E_value_bit = P*4+S;
E_value = E >> E_value_bit & 0x1;