🍀簡介

在數據科學領域，線性回歸是一種基本而強大的統計分析方法。它廣泛應用于各個領域，從經濟學到生物醫學研究，從市場營銷到城市規劃，目的是建立和利用變量之間的簡單關系，以便預測未來趨勢或做出決策。在本文中，我們將深入探討簡單線性回歸的工作原理、應用場景和使用步驟，以幫助您更好地理解和應用這一強大的分析工具。

---

🍀什么是簡單線性回歸？

簡單線性回歸是一種線性回歸模型的基本形式，用于分析兩個變量之間的關系。其中一個變量被稱為“自變量”或“預測變量”，而另一個變量被稱為“因變量”或“響應變量”。簡單線性回歸假設自變量和因變量之間存在線性關系，即以自變量的值來預測因變量的值。

---

🍀簡單線性回歸的應用場景

• 預測銷售量：根據廣告投入金額預測產品銷售量。
• 理解變量之間的關系：比如研究學習時間和考試分數之間是否存在正相關關系。
• 預測趨勢：根據過去幾年的數據，預測未來的市場趨勢。

使用步驟：

• 收集數據：收集包含自變量和因變量的樣本數據。
• 數據預處理：對數據進行清洗，去除異常值或缺失數據。
• 繪制散點圖：可視化數據以了解自變量和因變量之間的總體關系。
• 擬合回歸線：使用最小二乘法擬合一條直線，使其最好地擬合數據分布。
• 解釋結果：根據回歸線的斜率和截距解釋變量之間的關系。
• 進行預測：利用已知自變量的值，通過回歸方程預測因變量的值。

注意事項：

• 線性回歸模型可能不適用于非線性關系的數據。
• 數據的質量對于回歸分析的準確性至關重要，要確保數據的準確性和一致性。
• 線性回歸模型的結果需要進行合理的解釋和驗證。

---

🍀代碼演示

上代碼前我們可以先了解一下最小二乘法

最小二乘法是一種常用的數學方法，用于擬合數據點與數學模型之間的關系。它的目標是通過調整模型的參數，使模型預測值與實際觀測值之間的誤差的平方和最小化。這種方法廣泛應用于統計學、機器學習、工程學和自然科學等領域，用于分析和擬合數據，尋找數據背后的模式和趨勢。

最小二乘法的基本思想是，通過最小化觀測值與模型預測值之間的殘差平方和來找到最優的模型參數。殘差是指每個觀測值與對應模型預測值之間的差異。通過求解最小化殘差平方和的問題，可以得到最優的模型參數。

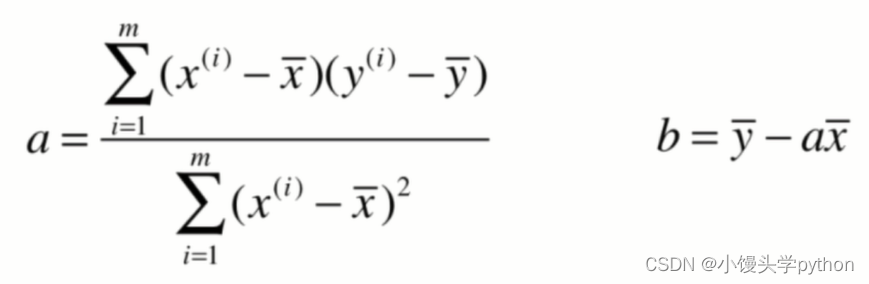
公式的推導可以看這位大佬的文章https://blog.csdn.net/weixin_40255714/article/details/125841394

import numpy as np
import matplotlib.pyplot as plt
x = np.array([1,2,3,4,5])
y = np.array([1,3,2,3,5])
plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()
#  y = a*x+b  需要計算出a和b
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0 # 分子
d = 0.0  #  分母
for x_i,y_i in zip(x,y):num += (x_i-x_mean)*(y_i-y_mean)d += (x_i-x_mean)**2
a = num/d
b = y_mean-a*x_mean

a和b求出來之后，我們就可以進行繪制一下，記住這里指的是找到一條直線，使得每一個點的預測值和真實值之差達到最小

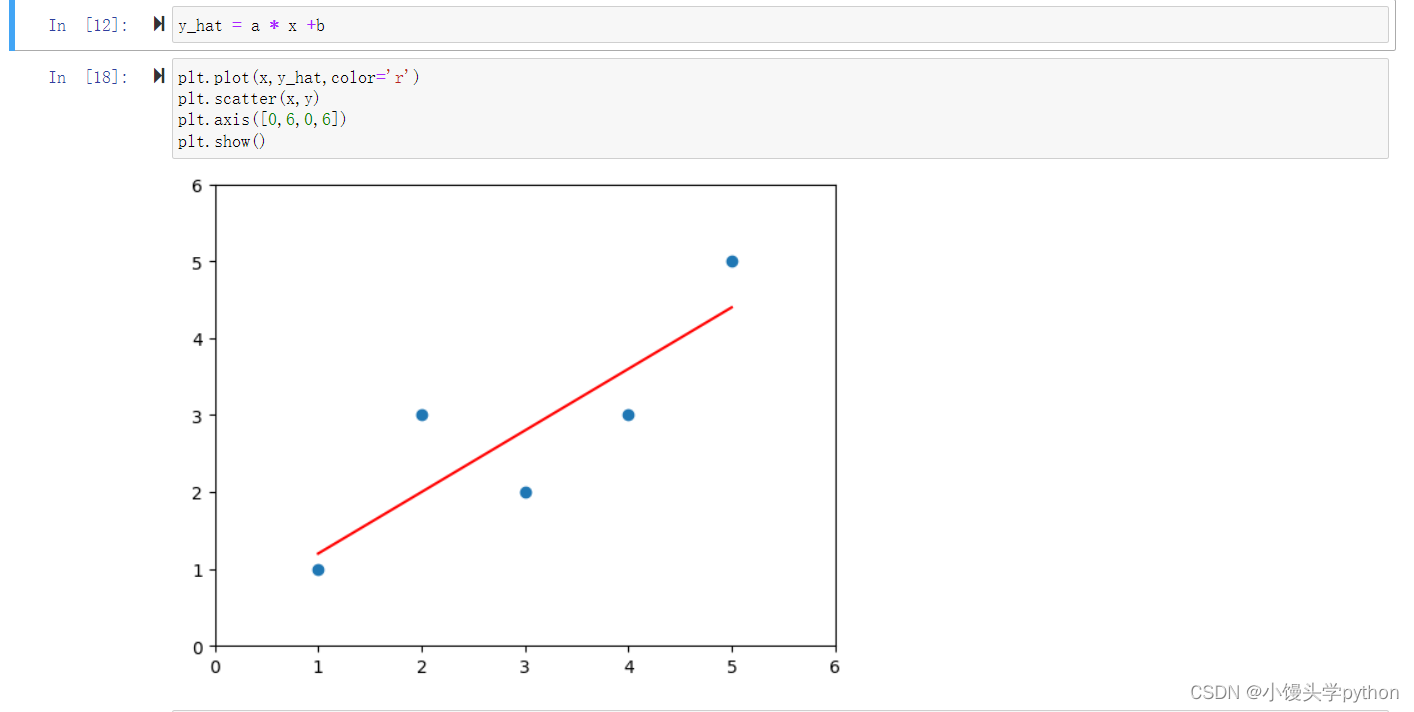
預測就很簡單了，帶入求值即可

🍀結論

簡單線性回歸是一種簡單而有效的分析方法，可用于預測和理解變量之間的關系。通過收集和處理數據，我們可以建立一個可靠的回歸模型，從而進行預測和決策。但要注意變量之間的線性關系是否真實存在，并且合理解釋結果。希望本文對您理解簡單線性回歸有所幫助，并且能夠在您的實際問題中應用這一強大的分析工具。

挑戰與創造都是很痛苦的，但是很充實。