數理統計：
數理統計是以概率論為基礎，研究社會和自然界中大量隨機現象數量變化基本規律的一種方法。分為：
描述統計
(描述統計的任務是搜集資料，進行整理、分組，編制次數分配表，繪制次數分配曲線，計算各種特征指標，以描述資料分布的集中趨勢、離中趨勢和次數分布的偏斜度等。)
推斷統計
(推斷統計是在描述統計的基礎上，根據樣本資料歸納出的規律性，對總體進行推斷和預測。)
概念
描述性統計，就是從總體數據中提取變量的主要信息(總和、均值等)，從而從總體層面上，對數據進行統計性描述。
在統計的過程中，通常會配合繪制相關的統計圖來進行輔助。
描述性統計所提取統計的信息，稱為統計量。
統計量
頻數與頻率
(數據的頻數與頻率統計適用于類別變量)
頻數
(數據中類別變量每個不同取值出現的次數)
頻率
(每個類別變量的頻數與總次數的比值，通常采用百分數表示)
e.g. 在n個變量中，類別變量a出現了m次(頻數)，頻率為m/n
集中趨勢分析
均值
(即平均值，其為一組數據的總和除以數據的個數)
中位數
(將一組數據升序排列，位于該組數據最中間位置的值。如果數據個數為偶數，則取中間兩個數值的均值)
眾數
(一組數據中出現次數最多的值)
分位數
(通過n-1個分位將數據劃分為n個區間，使得每個區間的數值個數相等，或近似相等。其中，n為分位數的數量。
常用的分位數有四分位數與百分位數)
以四分位數為例，通過3個分位，將數據劃分為4個區間
第1個分位稱為1/4分位(下四分位)。數據中1/4的數據小于該分位值
第2個分位稱為2/4分位(中四分位)。數據中2/4的數據小于該分位值
第3個分位稱為3/4分位(上四分位)。數據中3/4的數據小于該分位值
1.首先，計算四分位的位置
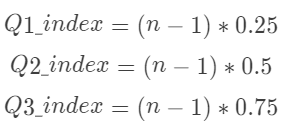(其中，位置index從0開始，n為數組中元素的個數)2.根據位置計算四分位值
⊙如果index為整數(小數點后為0)，四分位的值就是數組中索引為index的元素
⊙如果index不為整數，則四分位位置介于ceil(index)[向上取整]與floor(index)[向下取整]之間，根據這兩個位置的元素確定四分位值
離散程度分析
極差
(一組數據中，最大值與最小值之差)
方差
(一組數據中，每個元素與均值偏離的大小)
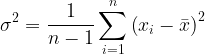
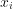：數組中的每個元素
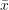：數組中所有元素的均值
：數組元素的個數
標準差
(方差的開方)
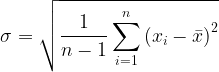
分布形狀
偏度
(是統計數據分布偏斜方向和程度的度量，是統計數據分布非對稱程度的數字特征)
如果數據對稱分布(例如正態分布) ? 偏度為0
如果數據左偏分布 ? 偏度小于0
如果數據右偏分布 ? 則偏度大于0
峰度
(是描述總體中所有取值分布形態陡緩程度的統計量，可理解為數據分布的高矮程度
峰度的比較是相對于標準正態分布的)
對于標準正態分布，峰度為0
如果峰度大于0，則密度圖高于標準正態分布
數據在分布上比標準正態分布密集，方差(標準差)較小
如果峰度小于0，則密度圖低于標準正態分布
數據在分布上比標準正態分布分散，方差(標準差)較大
變量
類別變量
(變量是一種分類，e.g. 顏色，性別，職位...)
無序類別變量
(無大小順序等級之分，又稱名義變量)
有序類別變量
(可按大小順序等級區分，又稱等級變量)
數值變量
(變量是一個具體的值，e.g. 1, 0.1...)
連續變量
(在一定區間內可以任意取值)
離散變量
(按一定順序一一列舉，通常以整數位取值的變量)
Q&A:
當數據中用0和1表示性別(或其他類別變量)時，此時0和1在實際意義上不做數值計算，應映射為類別變量。
均值、中位數與眾數：
數值變量通常使用均值與中值表示集中趨勢
類別變量通常使用眾數表示集中趨勢
在正態分布下，三者是相同的。在偏態分布下，三者會有所不同
均值使用所有的數據進行計算，因此容易受到極端值的影響
中位數與眾數不受極端值的影響，因此會相對穩定
眾數在一組數據中可能不是唯一的
三者的數量關系如下：
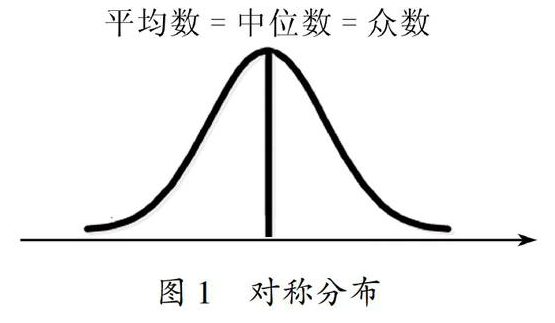
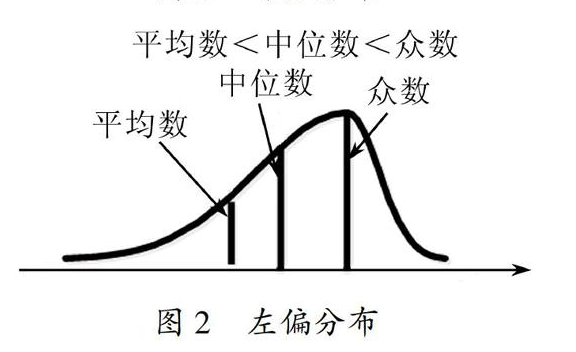
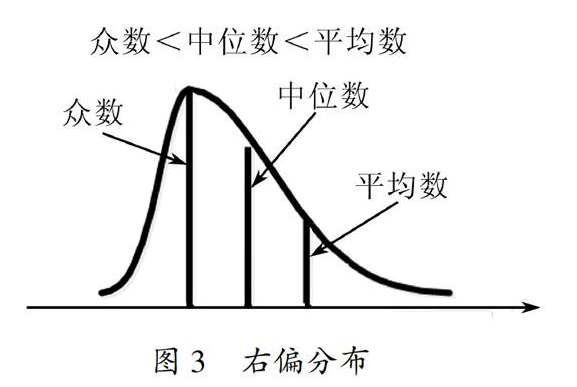
極差、方差與標準差：
極差的計算非常簡單，但是極差沒有充分的利用數據信息
方差(標準差)可以體現數據的分散性。方差(標準差)越大，數據越分散，方差(標準差)越小，數據越集中
方差(標準差)也可以體現數據的波動性(穩定性)。方差(標準差)越大，數據波動性越大，方差(標準差)越小，數據波動性越小
當數據較大時，也可以使用n代替n-1
代碼實現
import?numpy?as?np
import?pandas?as?pd
import?matplotlib.pyplot?as?plt
import?seaborn?as?sns
from?sklearn.datasets?import?load_iris
import?warnings
#?設置seaborn繪圖的樣式
sns.set(style?=?"darkgrid")
plt.rcParams["font.family"]?=?"SimHei"?#?正常顯示中文標簽
plt.rcParams["axes.unicode_minus"]?=?False?#?正常顯示負號
#?忽略警告信息
warnings.filterwarnings("ignore")
#?加載鳶尾花數據集
iris?=?load_iris()?#?dict[花萼的長度，花萼的寬度，花瓣的長度，花瓣的寬度]
# iris.data：鳶尾花數據集
# iris.target：每朵鳶尾花對應的類別(三種類別，取值為0,1,2)
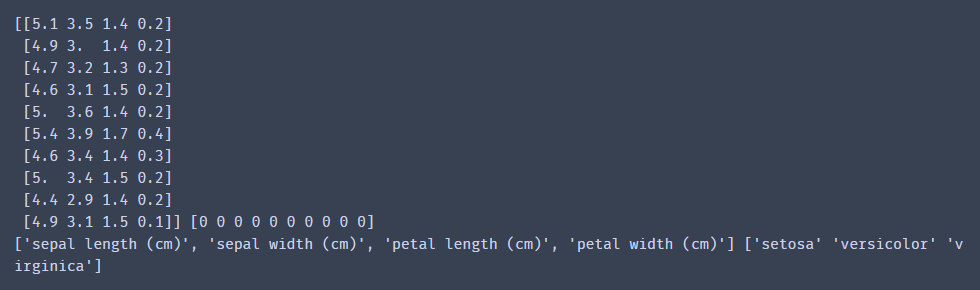
print(iris.data[0:10],iris.target[:10])?#?取前10條數據
# iris.feature_names：特征列的名稱
# iris.target_names：鳶尾花類別的名稱
print(iris.feature_names,iris.target_names)
輸出結果：
#?將鳶尾花數據與對應的類型合并，組合成完整的記錄
data?=?np.concatenate([iris.data,?iris.target.reshape(-1,1)],?axis=1)?#?橫向拼接
data?=?pd.DataFrame(data,?columns=["sepal_length","sepal_width","petal_length","petal_width","type"])
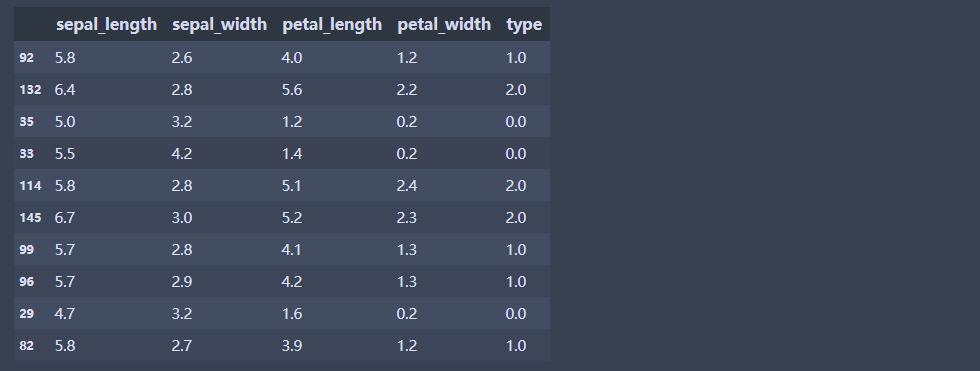
data.sample(10)?#?任意取出10條數據
輸出結果：
1頻數與頻率iris.target.reshape(? -1,1) ?表示將一維數組轉為二維數組
#?計算鳶尾花數據中，每個類別出現的頻數
frequency?=?data["type"].value_counts()
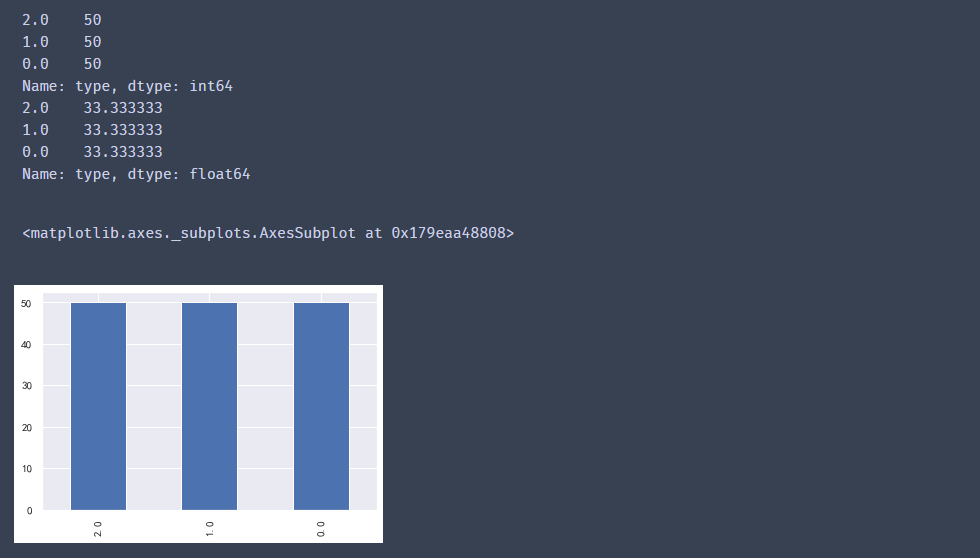
print(frequency)
#?計算每個類別出現的頻率，通常使用百分比表示
percentage?=?frequency?*?100?/?len(data)
print(percentage)
#?繪制條狀圖
frequency.plot(kind="bar")
輸出結果：
#?計算花萼長度的均值
mean?=?data["sepal_length"].mean()
#?計算花萼長度的中位數
median?=?data["sepal_length"].median()
#?方法一：計算花萼長度的眾數
s?=?data["sepal_length"].mode()
print(s)
#?注意：mode方法返回的是Series類型
mode?=?s.iloc[0]
print(mean,?median,?mode)
#?方法二：使用scipy中的stats模塊獲取花萼長度的眾數
from?scipy?import?stats
stats.mode(data["sepal_length"]).mode
#?繪制數據的分布(直方圖+密度圖)
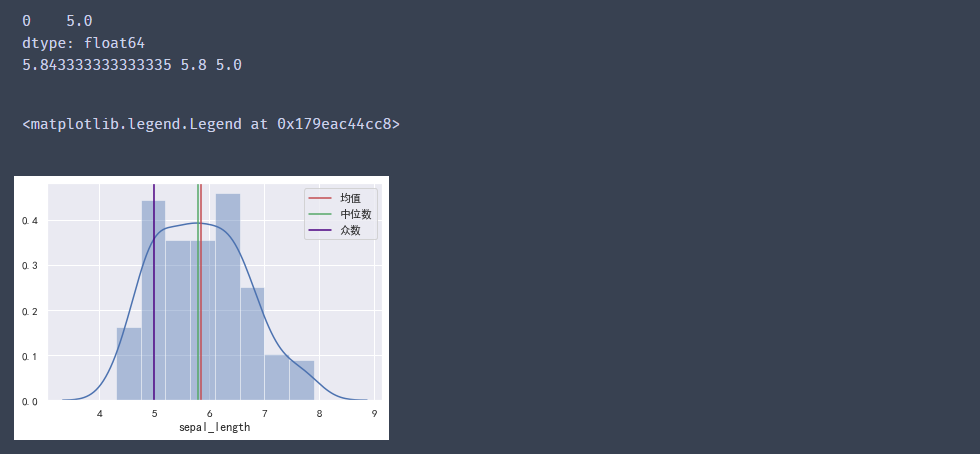
sns.distplot(data["sepal_length"])
#?繪制垂直線
plt.axvline(mean,?ls="-",?color="r",?label="均值")
plt.axvline(median,?ls="-",?color="g",?label="中位數")
plt.axvline(mode,?ls="-",?color="indigo",?label="眾數")
plt.legend()
輸出結果：
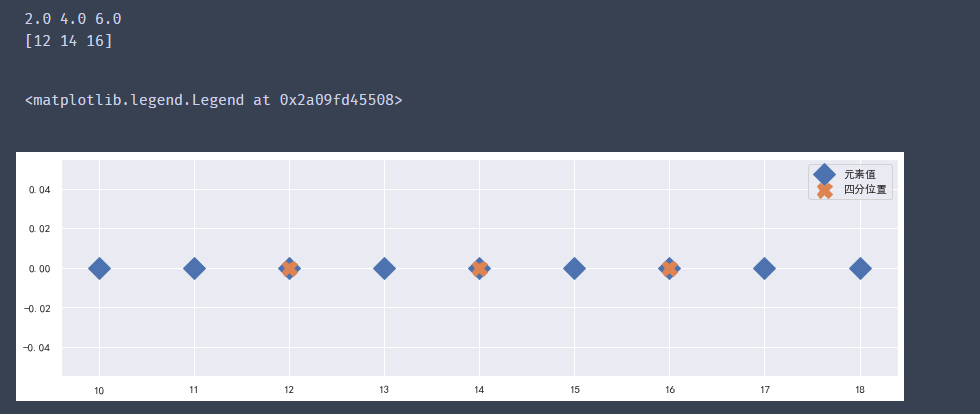
#?index為整數的情況
x?=?np.arange(10,19)
n?=?len(x)
#?計算四分位的索引(index)
q1_index?=?(n-1)?*?0.25
q2_index?=?(n-1)?*?0.5
q3_index?=?(n-1)?*?0.75
print(q1_index,?q2_index,?q3_index)
#?將index轉換成整數類型
index?=?np.array([q1_index,?q2_index,?q3_index]).astype(np.int32)
print(x[index])
plt.figure(figsize=(15,4))
plt.xticks(x)
plt.plot(x,?np.zeros(len(x)),?ls="",?marker="D",?ms=15,?label="元素值")
plt.plot(x[index],?np.zeros(len(index)),?ls="",?marker="X",?ms=15,?label="四分位置")
plt.legend()
輸出結果：
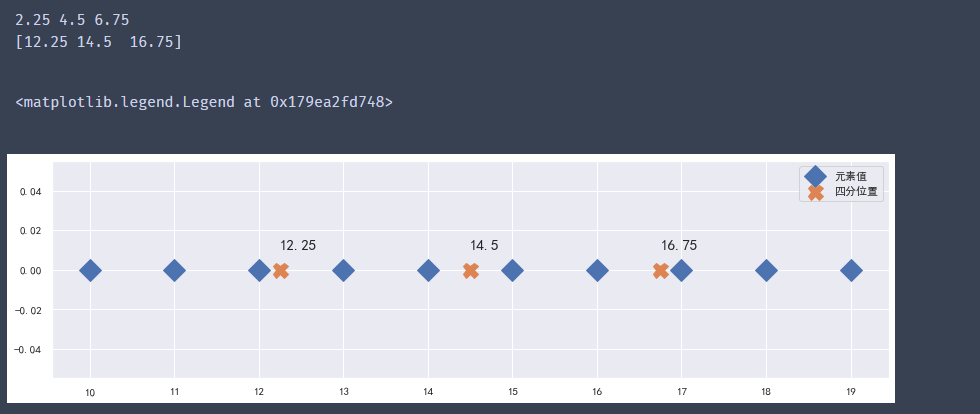
#?index不為整數的情況
x?=?np.arange(10,20)
n?=?len(x)
q1_index?=?(n-1)?*?0.25
q2_index?=?(n-1)?*?0.5
q3_index?=?(n-1)?*?0.75
print(q1_index,?q2_index,?q3_index)
#?使用該值臨近的兩個整數來計算四分位置
index?=?np.array([q1_index,?q2_index,?q3_index])
#?計算index左邊的整數值
left?=?np.floor(index).astype(np.int32)
#?計算index右邊的整數值
right?=?np.ceil(index).astype(np.int32)
#?獲取index的小數部分與整數部分(整數部分不使用，變量名用下劃線)?
weight,?_?=?np.modf(index)
#?根據左右兩邊的整數，加權計算四分位數的值。權重與距離成反比
q?=?x[left]?*?(1-weight)?+?x[right]?*?weight
print(q)
plt.figure(figsize=(15,4))
plt.xticks(x)
plt.plot(x,?np.zeros(len(x)),?ls="",?marker="D",?ms=15,?label="元素值")
plt.plot(q,?np.zeros(len(q)),?ls="",?marker="X",?ms=15,?label="四分位置")
for?v?in?q:
????plt.text(v,?0.01,?s=v,?fontsize=15)
plt.legend()
輸出結果：
#?Numpy中計算分位數 np.quantile(x,?q)/np.percentile(x,?q)
x?=?[1,?3,?10,?15,?18,?20,?23,?40]
print(np.quantile(x,?q=[0.25,?0.5,?0.75]))
print(np.percentile(x,?q=[25,?50,?75]))
輸出結果：
quantile與percentile都可以計算分位數
quantile方法中 q(要計算的分位數)的取值范圍為[0,1]
percentile方法中 q 的取值范圍為[0,100]
#?Pandas中計算分位數 s.describe(percentiles)
x?=?[1,?3,?10,?15,?18,?20,?21,?23,?40]
s?=?pd.Series(x)
print(s.describe())輸出結果：
獲取四分之一分位的值的方法：
A. s.describe()[4]
B.?s.describe()["25%"]
C.?s.describe().iloc[4] (推薦使用)
D.?s.describe().loc["25%"](推薦使用)
E.?s.describe().ix[4]
F.?s.describe().ix["25%"]
4極差、方差以及標準差#?計算極差
sub1?=?data["sepal_length"].max()?-?data["sepal_length"].min()
sub2?=?np.ptp(data["sepal_length"])?
#?pandas?新版本中無法使用ptp()，舊版本的可以使用如下
#?sub2?=?data["sepal_length"].ptp()
#?計算方差
var?=?data["sepal_length"].var()
#?計算標準差
std?=?data["sepal_length"].std()
print(sub1,?sub2,?var,?std)
輸出結果：
#?構造左偏分布數據
t1?=?np.random.randint(1,?11,?size=100)
t2?=?np.random.randint(11,?21,?size=500)
t3?=?np.concatenate([t1,?t2])
left_skew?=?pd.Series(t3)
#?構造右偏分布數據
t1?=?np.random.randint(1,?11,?size=500)
t2?=?np.random.randint(11,?21,?size=100)
t3?=?np.concatenate([t1,?t2])
right_skew?=?pd.Series(t3)
#?計算偏度
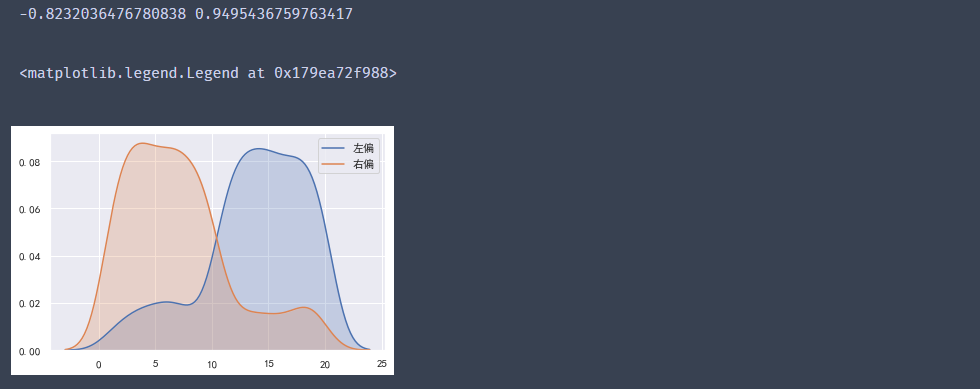
print(left_skew.skew(),?right_skew.skew())
#?繪制核密度圖
sns.kdeplot(left_skew,?shade=True,?label="左偏")
sns.kdeplot(right_skew,?shade=True,?label="右偏")
plt.legend()
輸出結果：
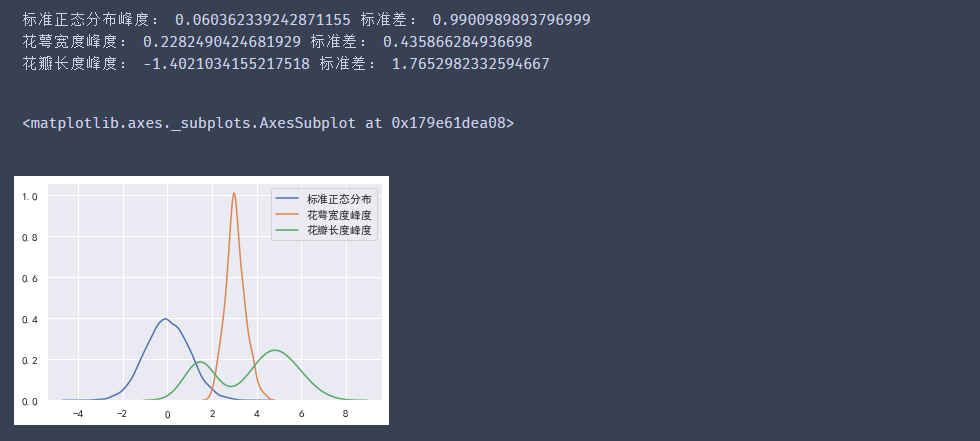
#?標準正態分布
standard_normal?=?pd.Series(np.random.normal(0,?1,?size=10000))
print("標準正態分布峰度：",?standard_normal.kurt(),?"標準差：",?standard_normal.std())
print("花萼寬度峰度：",?data["sepal_width"].kurt(),?"標準差：",?data["sepal_width"].std())
print("花瓣長度峰度：",?data["petal_length"].kurt(),?"標準差：",?data["petal_length"].std())
sns.kdeplot(standard_normal,?label="標準正態分布")
sns.kdeplot(data["sepal_width"],?label="花萼寬度峰度")
sns.kdeplot(data["petal_length"],?label="花瓣長度峰度")
輸出結果：
學習課程：開課吧-大數據分析全棧課程
