快速冪、矩陣快速冪、快速乘法

快速冪

快速冪是我們經常用到的一種算法，快速冪顧名思義就是快速的冪運算。我們在很多題目中都會遇到冪運算，但是在指數很大的時候，我們如果用for或者是pow就會超時，這時候就用到了快速冪。

快速冪的原理就是，當求b^p的時候，如果p是一個奇數，那么我們就可以把它拆成(b^2)^(p/2)*b，因此每次判斷一下是直接乘還是拆開就可以了。

洛谷模板鏈接：https://www.luogu.org/problemnew/show/P1226

下面是代碼：

#include<bits/stdc++.h>
using namespace std;
long long b,p,k;
void ksm(){long long ans=1,a=b,bb=b,pp=p;while(p){if(p&1) ans=ans*a%k; //判斷要不要拆開p>>=1; //p除以2a=a*a%k;}printf("%lld^%lld mod %lld=%lld",bb,pp,k,ans%k);
}
int main(){scanf("%lld%lld%lld",&b,&p,&k);ksm();return 0;
}

?

---

矩陣快速冪

矩陣快速冪顧名思義就是把快速冪的整數換成矩陣，要學習矩陣快速冪，就要先知道矩陣的乘法規則。矩陣的乘法規則由下圖所示：

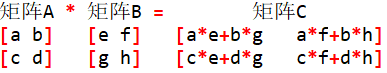
注意：兩個矩陣可以做乘法的條件是矩陣A的大小是N*M，矩陣B的大小是M*K，這樣的兩個矩陣相乘，得到矩陣C的大小是N*K。（通俗的說就是，第一個矩陣的列數等于另一個矩陣的行數）

矩陣的乘法有幾個性質是很重要的，必須記住，不要搞混：①矩陣乘法滿足乘法結合律 ②矩陣乘法滿足乘法分配律（包括左分配律和右分配律，左分配律是：C*(A+B)=CA+CB，右分配律是：(A+B)*C=AC+BC） ③矩陣乘法不滿足乘法交換律（例：AC!=CA）。

矩陣乘法的時間復雜度是O(NMK)的，下面是矩陣乘法的代碼：

?

for(i=1;i<=n;++i)for(j=1;j<=m;++j)for(l=1;l<=k;++l)c[i][l]+=a[i][j]*b[j][l];

?

注意：在做矩陣乘法的時候，最好是按照我上面代碼的循環順序計算，因為如果你改變了循環順序，速度就會變慢，如果你不相信的話可以去試一試，這是因為按照我代碼的順序，在計算一部分值之前，他的原值已經存在緩存中了，這樣的話是比從內存中讀取快的，而改變順序的話，就會從內存中調用，就會變慢了。

學會了矩陣乘法，矩陣快速冪就很輕松了。因為矩陣快速冪和快速冪的區別就在于，一個是整數的次方運算，一個是矩陣的次方運算。但需要注意的是，在矩陣相乘的時候，要存在第三方數組中，這樣才不會影響矩陣的值。

洛谷模板鏈接：https://www.luogu.org/problemnew/show/P3390

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=1000;
const ll mod = 1e9+7;
ll n,k,a[M][M],b[M][M],c[M][M];
void jz(int x){register int i,j,l;if(x==1){for(i=1;i<=n;++i)for(j=1;j<=n;++j)for(l=1;l<=n;++l)c[i][l]=(c[i][l]+a[i][j]*b[j][l]%mod)%mod;for(i=1;i<=n;++i)for(j=1;j<=n;++j)b[i][j]=c[i][j];memset(c,0,sizeof c);}else{for(i=1;i<=n;++i)for(j=1;j<=n;++j)for(l=1;l<=n;++l)c[i][l]=(c[i][l]+a[i][j]*a[j][l]%mod)%mod;for(i=1;i<=n;++i)for(j=1;j<=n;++j)a[i][j]=c[i][j];memset(c,0,sizeof c); //記住每次要清空
    }
}
void ksm(){while(k){if(k & 1) jz(1);k>>=1;jz(2);}
}
int main(){register int i,j;scanf("%lld",&n);scanf("%lld",&k);for(i=1;i<=n;++i)for(j=1;j<=n;++j)scanf("%lld",&a[i][j]),b[i][j]=a[i][j];--k; //因為在上一句中，在答案中已經有了矩陣A的一次方
    ksm();for(i=1;i<=n;++i){for(j=1;j<=n;++j)printf("%lld ",b[i][j]);printf("\n");}return 0;
}

?

---

?

快速乘法

快速乘法和快速冪的思想差不多，KSM是把a^p的p二進制分解，而快速乘法是把a*b的b分解，一般和KSM配套食用。當KSM%p會超范圍的時候，也就是取模之前就會乘爆，就要用到快速乘法。快速乘法就是把乘法改成加法，這樣一步一步的取模，就不會出現乘爆的問題了。

因為沒有找到例題，這里直接附上代碼：

typedef long long ll;
ll ksmul(ll x,ll y,int p){ //x*y%pll ans=0;while(y){if(y & 1) ans=(ans+y)%p;y>>=1;x=(x+x)%p;}return ans;
}

?