問題背景

高等數學應用非常廣，基本上涉及到函數的地方都要用到微積分，還有在幾何方面也是如此，計算機的應用讓我們能簡單快速處理各種高等數學中的計算，比如極限、導數、積分、微分方程等的計算。

實驗目的

使用 Python 通過計算與作圖，加強對極限、導數、積分等概念的理解，并掌握它們計算方法，以及求微分方程和方程組解析解的方法。

實驗原理與數學模型

1. 函數極限的求解討論以及兩個重要極限的驗證。
2. 導數概念和導數的幾何意義，以及計算多元函數偏導數和全微分的方法。
3. 一元函數積分學和多元函數積分學。
4. 微分方程和方程組在有無初始條件的分析。

實驗所用軟件

• Python 3.7
• NumPy 1.16.4
• SymPy 1.4
• Matplotlib 3.1.1

主要內容

1. 函數極限的求解和兩個重要極限的探究；
2. 導數、高階導數以及隱函數、參數方程定義函數導數的求解，多元函數偏導數和全微分的求解；
3. 計算定積分和不定積分以及重積分的方法；
4. 求解微分方程以及方程組解析解的方法。

實驗過程

1. 函數極限的求解和兩個重要極限

在這個實驗中我們通過對簡單的函數進行單側極限的求解，并且分析兩個重要極限。

例 1：考慮函數

解：編寫Python代碼如下：

import matplotlib.pyplot as plt

import numpy as np

import sympy as sp

# 求函數 y=arctan(1/x) 的左右極限

x = sp.Symbol('x')

fr = sp.atan(1 / x)

xl = sp.limit(fr, x, 0, dir='-')

xr = sp.limit(fr, x, 0, dir='+')

print('%s 左極限是：%s' % (fr, xl))

print('%s 右極限是：%s' % (fr, xr))

# 繪制函數 y=arctan(1/x) 的圖像

x = np.arange(-6, 6, 0.01)

y = np.arctan(1 / x)

plt.title('y=arctan(1/x)')

plt.plot(x, y)

plt.show()

運行代碼輸出結果和繪制圖像：

atan(1/x) 左極限是：-pi/2

atan(1/x) 右極限是：pi/2

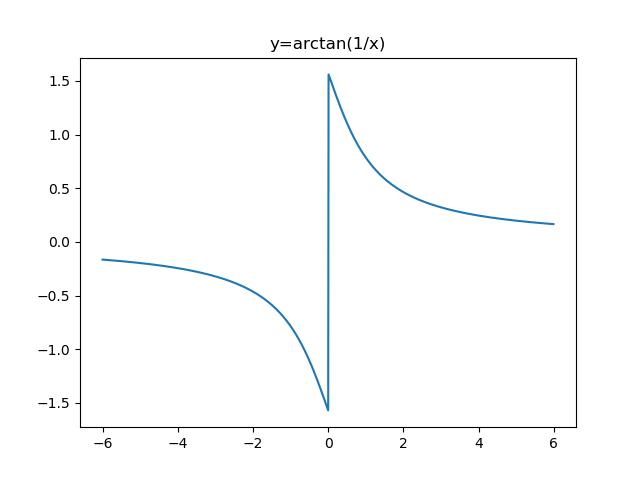
根據計算結果和繪制的圖像分析求得出題中函數的左右極限分別為 -pi/2 和 pi/2 。

例 2：兩個重要極限的驗證。

解：編寫Python代碼如下：

import matplotlib.pyplot as plt

import numpy as np

import sympy as sp

# 分析兩個重要極限

x = sp.Symbol('x')

f1 = sp.sin(x) / x

f2 = (1 + 1 / x) ** x

x1 = sp.limit(f1, x, 0)

x2 = sp.limit(f2, x, 'oo')

print('%s 第一重要極限的值：%s' % (f1, x1))

print('%s 第二重要極限的值：%s' % (f2, x2))

# 繪制函數圖像分析兩個重要極限

x1 = np.arange(-3, 3, 0.01)

x2 = np.arange(0.01, 100, 0.1)

y1 = np.sin(x1) / x1

y2 = (1 + 1 / x2) ** x2

plt.figure(figsize=(12, 5))

plt.subplot(121)

plt.title('y=sin(x)/x')

plt.plot(x1, y1)

plt.subplot(122)

plt.title('y=(1+1/x)**x')

plt.plot(x2, y2)

plt.show()

運行代碼輸出結果和繪制圖像：

sin(x)/x 第一重要極限的值：1

(1 + 1/x)**x 第二重要極限的值：E

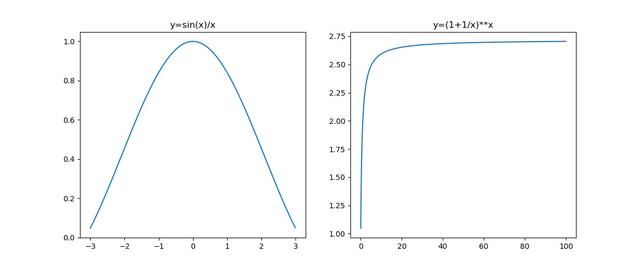
根據上圖變化趨勢理解函數極限和程序得出的答案，驗證兩個重要極限。

2. 導數與微分的研究

在這個實驗中，我們探究導數概念及其幾何意義，高階導數，隱函數導數，參數方程定義的函數導數，以及求解多元函數偏導數和全微分。

例 1：求 f(x)=2x^3+3x^2-12x+7 的導函數，并作出該函數圖形和在 x=-1 處的切線。

解：編寫Python代碼如下：

import matplotlib.pyplot as plt

import numpy as np

import sympy as sp

# 導數與微分

x = sp.Symbol('x')

f = 2 * x ** 3 + 3 * x ** 2 - 12 * x + 7

d = sp.diff(f)

print('%s 的導函數為：%s' % (f, d))

y_d = d.evalf(subs={x: -1})

y_h = f.evalf(subs={x: -1})

print('將x=-1代入導函數求解為：%d' % y_d)

print('將x=-1代入原函數求解為：%d' % y_h)

f_d = y_d * (x + 1) + y_h

print('得出切線方程為：%s' % f_d)

# 繪制函數圖和切線圖

x = np.arange(-4, 3, 0.01)

y1 = 2 * x ** 3 + 3 * x ** 2 - 12 * x + 7

y2 = 8 - 12 * x

plt.title('函數y=2*x**3+3*x**2-12*x+7以及當x=-1時的切線')

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

plt.plot(x, y1, x, y2)

plt.show()

運行代碼輸出結果和繪制圖像：

2*x**3 + 3*x**2 - 12*x + 7 的導函數為：6*x**2 + 6*x - 12

將x=-1代入導函數求解為：-12

將x=-1代入原函數求解為：20

得出切線方程為：8.0 - 12.0*x

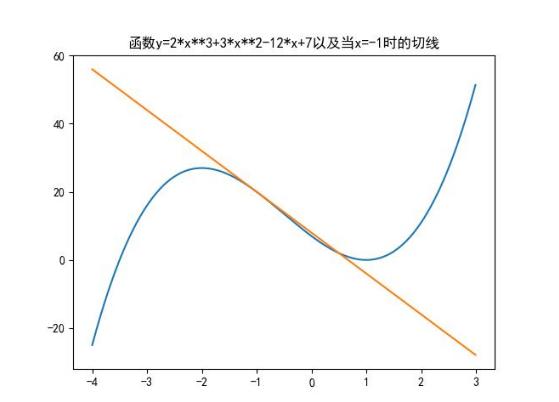
最后執行便在同一個坐標系內作出了函數 f(x) 的圖形和它在 x=-1 處的切線(直線為切線)。

注：此兩行代碼是為了解決在繪圖中顯示中文亂碼的問題。

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

例 2：求函數 y=x^{10}+2(x-10)^9 的1階到11階導數。

解：編寫Python代碼如下：

import sympy as sp

x = sp.Symbol('x')

y = x ** 10 + 2 * (x - 10) ** 9

for n in range(1, 12):

y = d = sp.diff(y)

print('第%2d階導數為：%s' % (n, d))

輸出即為題中要求所得函數高階導數。

例 3：求由方程 2x^2-2xy+y^2+x+2y+1=0 確定的隱函數的導數。

解：編寫Python代碼如下：

import sympy as sp

x, y = sp.symbols('x y')

z = 2 * x ** 2 - 2 * x * y + y ** 2 + x + 2 * y + 1

d = -sp.diff(z, x) / sp.diff(z, y)

print('原方程導數為：%s' % d)

運行代碼輸出結果：

原方程導數為：(-4*x + 2*y - 1)/(-2*x + 2*y + 2)

該實驗根據隱函數求導公式 dy/dx=-Fx/Fy 求得，然后再根據一般求導公式即可求出結果。

例 4：求由參數方程 x=e^tcos(t), y=e^tsin(t) 確定的函數的導數。

解：編寫Python代碼如下：

import sympy as sp

t = sp.Symbol('t')

x = sp.exp(t) * sp.cos(t)

y = sp.exp(t) * sp.sin(t)

d = sp.diff(y, t) / sp.diff(x, t)

print('原參數方程導數結果為：%s' % d)

d = sp.simplify(d)

print('原參數方程導數化簡為：%s' % d)

運行代碼輸出結果：

原參數方程導數結果為：(exp(t)*sin(t) + exp(t)*cos(t))/(-exp(t)*sin(t) + exp(t)*cos(t))

原參數方程導數化簡為：tan(t + pi/4)

根據參數方程求導法則最后求得由參數方程確定函數的導數。

例 5：設 z=sin(xy)+cos^2(xy) ，求偏導數(省略數學公式，點擊閱讀原文查看)。

解：編寫Python代碼如下：

import sympy as sp

x, y = sp.symbols('x y')

z = sp.sin(x * y) + (sp.cos(x * y)) ** 2

d1 = sp.diff(z, x)

d2 = sp.diff(z, y)

d3 = sp.diff(z, x, 2)

d4 = sp.diff(sp.diff(z, x), y)

print('第一偏導數為：%s' % d1)

print('第二偏導數為：%s' % d2)

print('第三偏導數為：%s' % d3)

print('第四偏導數為：%s' % d4)

運行代碼輸出結果：

第一偏導數為：-2*y*sin(x*y)*cos(x*y) + y*cos(x*y)

第二偏導數為：-2*x*sin(x*y)*cos(x*y) + x*cos(x*y)

第三偏導數為：y**2*(2*sin(x*y)**2 - sin(x*y) - 2*cos(x*y)**2)

第四偏導數為：2*x*y*sin(x*y)**2 - x*y*sin(x*y) - 2*x*y*cos(x*y)**2 - 2*sin(x*y)*cos(x*y) + cos(x*y)

以上為多元函數偏導數的結果。

3. 定積分與不定積分以及重積分的研究

在這個實驗中，我們研究定積分與不定積分的計算，以及多重積分的計算，深入理解曲線積分、曲面積分的概念個計算方法。

例 1：計算 int{sqrt{4-x^2}dx} 和 int_1^2{sqrt{4-x^2}} 。

解：編寫Python代碼如下：

import sympy as sp

x = sp.Symbol('x')

y = sp.sqrt(4 - x ** 2)

i1 = sp.integrate(y, x)

i2 = sp.integrate(y, (x, 1, 2))

print('不定積分的結果為：%s' % i1)

print('定積分的結果為：%s' % i2)

運行代碼輸出結果：

不定積分的結果為：x*sqrt(4 - x**2)/2 + 2*asin(x/2)

定積分的結果為：-sqrt(3)/2 + 2*pi/3

使用 Python 求解不定積分時，會省略積分的常數。

例 2：計算三重積分 iiint{(x^2+y^2+z)dxdydz} ，其中由曲面 z=sqrt{2-x^2-y^2} 與 z=sqrt{x^2+y^2} 圍成。

解：編寫Python代碼作出區域曲面圖形，如下：

import matplotlib.pyplot as plt

import numpy as np

from mpl_toolkits.mplot3d import Axes3D

x = np.arange(-1, 1, 0.05)

y = np.arange(-1, 1, 0.05)

x, y = np.meshgrid(x, y)

z1 = np.sqrt(x ** 2 + y ** 2)

z2 = np.sqrt(2 - x ** 2 - y ** 2)

ax = Axes3D(plt.figure())

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

ax.set_title('三重積分曲面')

ax.plot_surface(x, y, z1)

ax.plot_surface(x, y, z2)

plt.show()

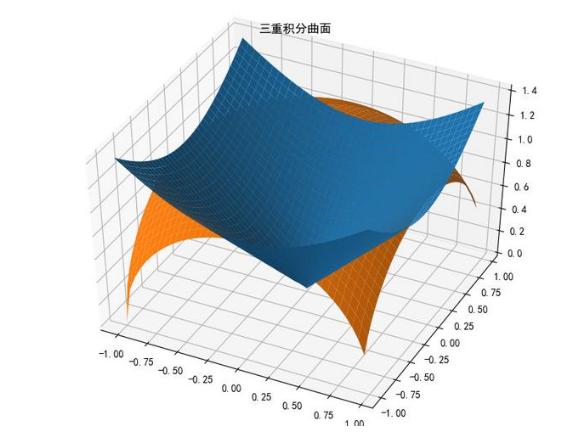
將方程轉換為柱坐標計算，然后確定積分限，編寫Python代碼：

import sympy as sp

r, s, z = sp.symbols('r s z')

f = (r ** 2 + z) * r

i = sp.integrate(sp.integrate(sp.integrate(f, (z, r, sp.sqrt(2 - r ** 2))), (r, 0, 1)), (s, 0, 2 * sp.pi))

print('三重積分計算結果為：%s' % i)

運行代碼輸出結果：

三重積分計算結果為：2*pi*(-5/12 + 8*sqrt(2)/15)

4. 求微分方程的解析解

在這個實驗中，我們用通過 Python 來求解微分方程的通解，在初始條件下的特解，以及微分方程組在初始條件下的特解。

例 1：求微分方程 y'+2xy=xe^{-x^2}

解：編寫Python代碼如下：

import sympy as sp

x = sp.Symbol('x')

f = sp.Function('f')

y = f(x)

d = sp.Eq(y.diff(x) + 2 * x * y, x * sp.exp(-x ** 2))

diff = sp.dsolve(d, y)

print('微分方程的通解為：%s' % diff)

運行代碼輸出結果：

微分方程的通解為：Eq(f(x), (C1 + x**2/2)*exp(-x**2))

例 2：求微分方程 xy'+y-e^{-x}=0 在初始條件 y(x=1)=2e 下的特解。

解：編寫Python代碼如下：

import sympy as sp

x = sp.Symbol('x')

f = sp.Function('f')

y = f(x)

d = sp.Eq(x * y.diff(x) + y - sp.exp(-x), 0)

diff = sp.dsolve(d, y, ics={f(1): 2 * sp.exp(1)})

print('微分方程的特解為：%s' % diff)

運行代碼輸出結果：

微分方程的特解為：Eq(f(x), ((1 + 2*exp(2))*exp(-1) - exp(-x))/x)ga