1.什么是線性回歸?
用線性關系去擬合輸入和輸出。
設輸入為x,則輸出y=ax+b。
對于多元的情況y=b×1+a1x1+a2x2+...+anxn。
用θ表示系數,可以寫作:

其中,x0=1。
2.線性回歸有什么用?
對于連續輸入和輸出的問題,如果線性回歸可以較好的擬合輸入和輸出,那么可以用這個模型預測其它輸入時的輸出。
反過來想:如果線性回歸可以較好的擬合輸入和輸出,那么說明輸出和輸入有很強的線性相關性,可以識別輸入中的冗余信息。
3.怎么判斷是否較好的擬合?
初步考慮,就是當使用模型時的輸出、和真實的輸出有多大偏差,選擇一個方法量化這個偏差。
每個樣本輸入模型時,均會產生一個偏差。
線性回歸中,通過求這些偏差的平方平均值,來判斷偏差的程度。寫作:
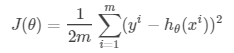
其中實際輸出為y,模型輸出為h,上標i是指每個樣本。系數在平方平均值的基礎上除以2。
判斷偏差的這個方程起名叫 Cost Function。當偏差越小、即Cost Function的值越小時,擬合的越好。?
4.怎么訓練模型?
訓練模型的目的在于實現較好的擬合,也就是說使Cost Function的值盡量小。
訓練在這里,就是選擇一組系數θ(模型確定以后,模型的參數就是系數θ們),實現上面的目的。
微積分學過,可以對θ求偏導數等于0的點,直接得到極值點。
按照Andrew Ng的課件,當參數個數大于10000個時,直接求極值點時間太長,需要選擇別的辦法。
5.怎樣訓練模型:梯度下降。
顧名思義,就是沿著梯度下降。選擇一個合適的步長α,一步一步改變θ,使Cost Function的值不斷減小。
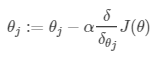
其中,θj表示各個系數。:=前面的冒號表示每個θj同時改變。
走多少步?和怎么判斷模型訓練好了呢?最好是觀察每次θj改變后,J(θ)的值的變化。
最開始θj等于多少呢?最開始,隨便選一組值就可以。
步長α應該選多大呢?要通過手動嘗試,“找”到合適的值。
最后,經過多次迭代后,算法得到一組θ,使Cost Function的值比較小。
6.matlab實現一個線性回歸。
%一個特征的輸入參數
X1=[0.50,0.75,1.00,1.25,1.50,1.75,1.75,2.00,2.25,2.50,2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50];
X0=ones(size(X1));
X=([X0;X1])';
y=([10, 22, 13, 43, 20, 22, 33, 50, 62, 48, 55, 75, 62, 73, 81, 76, 64, 82, 90, 93])';
%梯度下降參數設計
alpha=0.001;%當alpha大于1時就不收斂了
theta=[2;3];%選哪個點作為起點似乎對收斂速度影響不大
times=2000;%迭代次數
for i=1:times
delta=X*theta-y;%求偏導數
theta=theta-alpha.*(X'*delta);%梯度下降
J(i)=delta'*delta;%求此時的Cost Function值
end
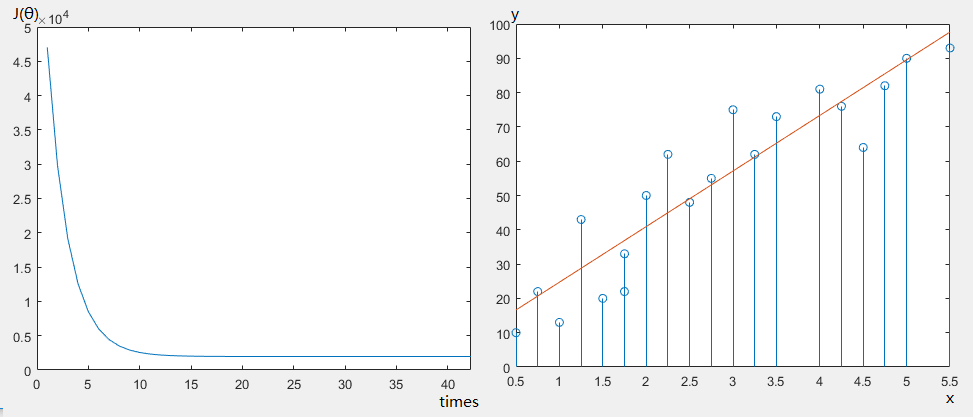
%觀察Cost Function值隨迭代次數的變化
% plot(J);
%觀察擬合情況
stem(X1,y);
p2=X*theta;
hold on;
plot(X1,p2);
?
7.實際使用
實際使用線性回歸時,先對輸入數據進行優化。包括:1.將冗余的和無關的變量去掉;2.對于非線性關系,采用多項式擬合,將一個變量變為多個變量;3.將輸入范圍歸一化。
?
小結
線性回歸開始假設輸入和輸出存在線性關系,
然后使用線性回歸模型h=θTx,用Cost Function J(θ)評價擬合程度,
通過對J(θ)應用梯度下降算法逼近一組好的參數θ,從而得到一個適用的模型h。
?
線性回歸的使用建立在“輸入和輸出存在線性關系”這一假設基礎上,把一組特征映射到一個值。
使用起來,也許因為模型太簡單,感覺不到“機器學習”的感覺。選用時也需要很多先驗知識、針對特定情況,就像一般的編程處理問題一樣。
在使用梯度下降的算法時,迭代的過程,有點“學習”的感覺。

網際控制報文協議初識)














1——10題)
)

